|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Специальные методы сортировки
Сортирующие сети
Простейшей моделью для изучения неадаптивных алгоритмов сортировки является абстрактная машина, которая обращается к данным только с помощью операций сравнения-обмена. Такая машина называется сортирующей сетью (sorting network). Сортирующая сеть построена из простых неделимых модулей сравнения-обмена (compare-exchange module), или компараторов (comparator), соединенных между собой таким образом, что возможно выполнение полной сортировки общего вида.
Ключи перемещаются по линиям сортирующей сети слева направо. По пути им встречаются компараторы, которые при необходимости обменивают ключи, в результате чего меньший из двух ключей поднимается на верхнюю линию. В данном примере на двух верхних линиях обмениваются ключи B и C, потом на двух нижних линиях обмениваются A и D, затем обмениваются A и B и т.д., и в конце ключи оказываются упорядоченными сверху вниз. В этом примере обмен ключей выполняют все компараторы, за исключением четвертого. Такая сеть способна отсортировать любые перестановки из четырех ключей.
На рис. 11.4 показана простая сортирующая сеть для четырех ключей. Обычно сортирующая сеть для N элементов изображается в виде последовательности N горизонтальных прямых линий и компараторов, соединяющих пары этих линий. Сортируемые ключи как бы проходят по сети слева направо, а если встречается компаратор, он при необходимости производит обмен этих чисел, чтобы меньшее из двух чисел оказалось вверху.
До построения реальной сортирующей машины, работающей по этой схеме, нужно решить ряд вопросов. Например, не описан метод кодирования входных данных. Один из способов - рассматривать каждую линию связи на рис. 11.4 как группу линий, передающих по одному биту данных, так что все биты ключа распространяются по линии одновременно. Другой подход заключается в том, что данные поступают на входы компараторов по одной линии бит за битом (сначала наиболее значащие биты). Кроме того, совершенно не затронут вопрос синхронизации: должны быть предусмотрены механизмы, препятствующие срабатыванию компараторов до готовности входных данных. Сортирующие сети - это полезные абстракции, поскольку они позволяют нам отделять детали реализации от проектных решений более высокого уровня наподобие минимизации количества компараторов. Более того, как мы убедимся в разделе 11.5, абстракция сортирующей сети может быть полезной и в приложениях, отличных от построения непосредственно электронных схем.
Еще одним важным применением сортирующих сетей является использование их в качестве модели параллельных вычислений. Если два компаратора не используют для ввода данных одни и те же линии, то, очевидно, они могут работать одновременно. Например, сеть, изображенная на рис. 11.4, показывает, что четыре элемента могут быть отсортированы за три параллельных шага. На первом шаге могут одновременно работать компаратор 0-1 и компаратор 2-3, после чего на втором шаге могут одновременно работать компаратор 0-2 и компаратор 1-3, и на третьем шаге компаратор 2-3 завершает сортировку. Для любой заданной сети компараторы нетрудно сгруппировать в последовательность параллельных каскадов (parallel stage), состоящих из компараторов, которые могут работать одновременно (см. упражнение 11.17). Для наибольшей эффективности параллельных вычислений нужно разрабатывать сети с минимально возможным числом параллельных каскадов.
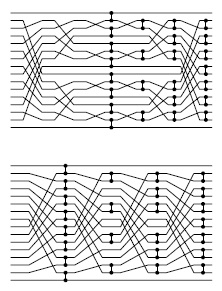
Программа 11.2 непосредственно соответствует сливающей сети для каждого N, но полезно ознакомиться и с прямым восходящим построением, изображенным на рис. 11.5.
Показанные на этом рисунке различные представления сетей на четыре (вверху), восемь (в центре) и 16 (внизу) линий демонстрируют рекурсивную структуру, на которой основаны сети. Слева показаны непосредственные представления построения сети размера N с помощью двух копий сетей размера N/2 (одна для линий с четными номерами, другая для линий с нечетными номерами) плюс каскад компараторов между линиями 1 и 2, 3 и 4, 5 и 6 и т.д. Справа показаны более простые сети, полученные из сетей, изображенных слева, путем группирования компараторов одинаковой длины. Такое группирование возможно потому, что компараторы на нечетных линиях можно перемещать независимо от компараторов на нечетных линиях.
Программа 11.3. Нечетно-четное слияние Бэтчера (нерекурсивная версия)
Данная реализация нечетно-четного слияния Бэтчера (в которой предполагается, что размер файла N является степенью 2) компактна, но непонятна. Понять, как она выполняет слияние, можно, сравнив ее с рекурсивной версией (см. программу 11.2 и рис. 11.5). Она совершает слияние за lgN проходов, состоящих из единообразных и независимых инструкций сравнения-обмена.
template <class Item>
void merge(Item a[], int l, int m, int r)
{ int N = r-l+1; // предполагается,
// что N/2 равно m-l+1
for (int k = N/2; k > 0; k /= 2)
for (int j = k % (N/2); j+k < N; j += k+k)
for (int i = 0; i < k; i++)
compexch(a[l+j+i], a[l+j+i+k]);
}
Для создания сливающей сети размера N мы воспользуемся двумя копиями сети размером N/2: одна для линий с четными номерами, а другая - с нечетными. Поскольку эти два множества компараторов не пересекаются, их можно распределить таким образом, чтобы обе сети чередовались. И в завершение мы расставим компараторы между линиями 1 и 2, 3 и 4 и т.д. Чередование нечетных и четных линий заменяет идеальное тасование из программы 11.2. Доказательство того, что эти сети выполняют слияние правильно, аналогично доказательствам свойств 11.1 и 11.2 с помощью принципа нулей и единиц. На рис. 11.6 показан пример выполнения такого слияния.
Если удалить все операции тасования, то для выполнения слияния Бэтчера в данном примере требуется 25 изображенных здесь операций слияния-обмена. Их можно разбить на четыре фазы выполнения независимых операций сравнения-обмена с фиксированным сдвигом каждой фазы.
Программа 11.3 является восходящей реализацией слияния Бэтчера без тасования; она соответствует сетям, представленным на рис. 11.5. Эта программа представляет собой компактный и элегантный обменный метод слияния, который, возможно, лучше считать альтернативным представлением сетей, хотя прямое доказательство того, что она правильно выполняет задачу слияния, интересно и само по себе. Одно такое доказательство будет рассмотрено в конце этого раздела.
На рис. 11.7 показана нечетно-четная сортирующая сеть Бэтчера, построенная на основе сетей слияния, которые показаны на рис. 11.5, с помощью стандартного построения рекурсивной сортировки слиянием. Все построение дважды рекурсивно: один раз для сливающих сетей, другой - для сортирующих сетей. Они не оптимальны (мы вскоре рассмотрим оптимальные сети), но тем не менее они эффективны.
Данная сортирующая сеть на 32линии содержит две копии сетей на 16линий, четыре копии сетей на восемь линий и т.д. Просматривая эту структуру справа налево, мы как бы глядим на нее сверху вниз: сортирующая сеть на 32линии состоит из сливающей сети 16-и-16, за которой следуют две копии сортирующей сети на 16 линий (для верхней половины и для нижней половины). Каждая сеть на 16 линий состоит из сливающей сети 8-и-8, за которой следуют две копии сортирующей сети на 8 линий и т.д. Просматривая эту структуру слева направо, мы как бы глядим на нее снизу вверх: первый столбец компараторов создает упорядоченные файлы размером 2; далее идут сливающие сети 2-и-2, создающие отсортированные подфайлы размером 4; затем идут сливающие сети 4-и-4, создающие отсортированные подфайлы размером 8 и т.д.
Лемма 11.3. Нечетно-четные сортирующие сети Бэтчера используют порядка N (lgN)2 / 4 компараторов и могут выполнить сортировку за (lgN)2 / 2 параллельных шагов.
Сливающие сети требуют выполнения порядка lgN параллельных шагов, а сортирующим сетям нужно 1 + 2 + ... + lgN, или порядка
(lgN)2 / 2
, параллельных шагов. Подсчет компараторов оставлен читателю в качестве упражнения (см. упражнение 11.23). 
Использование функции слияния из программы 11.3 в стандартной рекурсивной сортировке слиянием, представленной программой 8.3, дает компактный обменный метод сортировки, который является неадаптивным и использует O (N (lgN)2) операций сравнения-обмена. С другой стороны, из сортировки слиянием можно удалить рекурсию и непосредственно реализовать полную восходящую версию, как показано в программе 11.4. Как и в случае программы 11.3, эту программу легче понять, если рассматривать ее как альтернативное представление сети, показанной на рис. 11.7.
В этой реализации в программу 11.3 добавлены еще один цикл и одна проверка, поскольку слияние и сортировка обладают похожими рекурсивными структурами. Для выполнения восходящего прохода слияния последовательности отсортированных файлов размера 2k в последовательность отсортированных файлов размера 2k+1 используется вся сливающая сеть, но при этом включаются только те компараторы, которые полностью попадают в подфайлы. Данная программа претендует на звание наиболее компактной нетривиальной реализации сортировки, какую нам когда-либо приходилось видеть и которая может оказаться наилучшим выбором в тех случаях, когда мы хотим воспользоваться всеми преимуществами высокопроизводительных архитектурных особенностей для разработки скоростной сортировки небольших файлов (или для построения сортирующей сети). Если бы мы не рассмотрели до этого различные рекурсивные реализации и сетевые построения, то понимание того, как и почему выполняет упорядочение рассматриваемая программа, могло бы оказаться непосильной задачей.
Программа 11.4. Нечетно-четная сортировка Бэтчера (нерекурсивная версия)
Данная реализация нечетно-четной сортировки Бэтчера непосредственно соответствует представлению сети на рис. 11.7. Она разбивается на фазы, индексируемые переменной p. Последняя фаза, где p равно N, является нечетно-четным слиянием Бэтчера. Предпоследняя фаза, где p равно N/2, является нечетно-четным слиянием с первым каскадом, в котором удалены компараторы, пересекающие N/2; третья с конца фаза, где p равно N/4, является нечетно-четным слиянием с двумя первыми каскадами, в котором удалены компараторы, пересекающие N/4, и т.п.
template <class Item>
void batchersort(Item a[], int l, int r)
{ int N = r-l+1;
for (int p = 1; p < N; p += p)
for (int k = p; k > 0; k /= 2)
for (int j = k%p; j+k < N; j += (k+k))
for (int i = 0; i < N-j-k; i++)
if ((j+i)/(p+p) == (j+i+k)/(p+p))
compexch(a[l+j+i], a[l+j+i+k]);
}
Как это часто бывает с методами " разделяй и властвуй " , в случае, когда N не равно степени 2, имеется две возможности (см. упражнения 11.24 и 11.21). Можно поделить файл пополам (нисходящий вариант), либо поделить по максимальной степени 2, меньшей N (восходящий вариант). Последний вариант для сортирующих сетей несколько удобнее, поскольку он эквивалентен построению полной сети для минимальной степени 2, большей или равной N, с последующим использованием только первых N линий и компараторов, подключенных к этим линиям обоими концами. Доказать, что это построение корректно, довольно просто. Предположим, что на неиспользуемые линии поданы сигнальные ключи, которые больше любых других ключей сети. Тогда компараторы на этих линиях никогда не производят операций обмена, и их можно спокойно удалить. Вообще-то можно воспользоваться любым набором из N смежных линий большей сети: достаточно считать, что на игнорируемых линиях в верхней части имеются сигнальные ключи с малыми значениями, а на игнорируемых линиях в нижней части - сигнальные ключи с большими значениями. Все эти сети содержат порядка N (lgN)2 / 4 компараторов.
Теория сортирующих сетей развивалась достаточно интересно (см. раздел ссылок). Задача построения сетей с минимально возможным числом компараторов была поставлена Бозе (Bose) еще до 1960 г., впоследствии она получила название задачи Бозе-Нельсона (Bose-Nelson). Сети Бэтчера были первым достаточно приемлемым решением этой задачи, и некоторое время даже считалось, что сети Бэтчера оптимальны. Сливающие сети Бэтчера оптимальны, и поэтому любая сортирующая сеть с существенно меньшим числом компараторов может быть построена только с помощью подхода, отличного от рекурсивной сортировки слиянием. Задача нахождения оптимальных сортирующих сетей не исследовалась до 1983 г., когда Аджтай (Ajtai), Комлос (Komlos) и Шемереди (Szemeredy) доказали существование сетей с O (Nlog N) компараторами. Однако сети AKS (Ajtai-Kolmos-Szemeredy) - это всего лишь математические построения, не имеющие практического применения, и сети Бэтчера все еще входят в число наиболее подходящих практических методов.
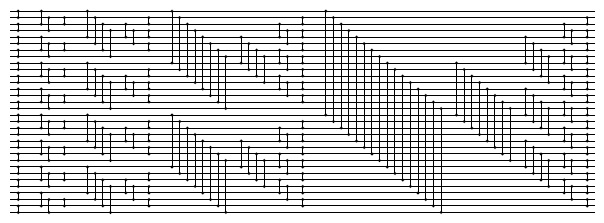
Связь между идеальным тасованием и сетями Бэтчера позволяет удивительным образом завершить рассмотрение сортирующих сетей анализом еще одной версии рассматриваемого алгоритма. Если перетасовать линии нечетно-четного слияния Бэтчера, то получатся сети, в которых все компараторы соединяют смежные линии. На рис. 11.8 показана сеть, которая соответствует реализации тасования, приведенной в программе 11.2. Такое переплетение соединений иногда называется сеть-бабочка (butterfly network). На этом рисунке дано еще одно представление той же линейной программы, обеспечивающее еще более однотипное переплетение; в нем используются только операции полного тасования.
Непосредственная реализация программы 11.2 в виде сортирующей сети порождает сеть, насыщенную рекурсивными операциями тасования и обратного тасования (вверху). Эквивалентная реализация (внизу) использует только полные тасования.