Орграфы и DAG-графы

Отношения эквивалентности и частичные порядки

В данном разделе излагаются фундаментальные понятия теории множеств и их взаимосвязь с алгоритмами абстрактного транзитивного замыкания. Они позволят нам рассмотреть изучаемые идеи в более широком контексте и продемонстрировать всю широту применения уже знакомых нам алгоритмов. Читатели с хорошей математической подготовкой, знакомые с теорией множеств, могут сразу перейти к разделу 19.5, поскольку излагаемый здесь материал элементарен (хотя может оказаться полезным краткий обзор терминологии). А читателям, не знакомым с теорией множеств, возможно, было бы полезно сначала ознакомиться с элементарными понятиями дискретной математики, так как наше изложение будет весьма лаконичным. Связь между орграфами и фундаментальными математическими понятиями достаточно важна, чтобы не игнорировать ее.

Пусть задано некоторое множество. Отношение (relation) между его объектами определяется как множество упорядоченных пар этих объектов. Не считая некоторых деталей, таких как параллельные ребра и петли, это определение совпадает с определением орграфа: отношения и орграфы — просто различные представления одной и той же абстракции. Математический вариант несколько более универсален, поскольку множества могут быть бесконечными, а все компьютерные программы работают с конечными множествами, но пока мы не будем обращать внимание на эти различия.

Обычно отношение обозначается символом R, а выражение sRt означает утверждение " упорядоченная пара (s, t) находится в отношении R " . Например, символ " < " используется для представления отношения " меньше чем " . Пользуясь этой терминологией, можно описывать различные свойства отношений. Например, отношение R называется симметричным, если для всех s и t из sRt следует tRs; отношение называется рефлексивным, если для всех s справедливо sRs. Симметричные отношения соответствуют неориентированным графам. Рефлексивные отношения соответствуют графам, в которых в каждой вершине есть петли; отношения, соответствующие графам, в которых ни у одной из вершин нет петель, называются нерефлексивными.

Говорят, что отношение транзитивно, когда из sRt и tRu следует sRu для всех s, t и и. Имеется и определение для транзитивного замыкания (transitive closure) отношения; однако мы не будем давать его определение в контексте теории множеств, а воспользуемся определением для орграфов из раздела 19.3. Любое отношение эквивалентно некоторому орграфу, а транзитивное замыкание отношения эквивалентно соответствующему транзитивному замыканию орграфа. Транзитивное замыкание любого отношения само транзитивно.

В контексте алгоритмов на графах для нас особо важны два специальных транзитивных отношения, которые определяются дополнительными ограничениями. Эти два вида широко распространенных отношений известны как отношения эквивалентности (equivalence relation) и частичные порядки (partial order).

Отношение эквивалентности (=) есть транзитивное отношение, которое к тому же рефлексивно и симметрично. Вообще-то симметричное и транзитивное отношение, которое помещает каждый объект в некоторую упорядоченную пару, должно быть и отношением эквивалентности: если s = t, то t = s (в силу симметричности), откуда s = s (в силу транзитивности). Отношение эквивалентности разбивает объекты множества на подмножества — классы эквивалентности (equivalence class). Два объекта s и t содержатся в одном и том же классе эквивалентности тогда и только тогда, когда s = t. Ниже приведены типичные примеры отношений эквивалентности:

Модульная арифметика. Любое положительное целое к определяет на множестве целых чисел отношение эквивалентности: s = t (mod к) тогда и только тогда, когда остаток от деления s на к равен остатку от деления t на к. Очевидно, что это отношение симметрично, а несложное рассуждение показывает, что оно еще и транзитивно (см. упражнение 19.67) — следовательно, оно является отношением эквивалентности.

Связность в графах. Отношение между вершинами " содержится в том же связном компоненте, что и... " есть отношение эквивалентности, поскольку оно симметрично и транзитивно. Классы эквивалентности соответствуют связным компонентам в графах.

При создании АТД графа, который позволяет клиентам проверять, находятся ли две вершины в одном и том же связном компоненте, мы реализуем АТД отношения эквивалентности, который предоставляет клиентам возможность проверки эквивалентности двух объектов. На практике это соответствие имеет большое значение, поскольку граф является сжатым представлением отношения эквивалентности (см. упражнение 19.71). Фактически, как мы видели в "Введение" и 18, для построения такого АТД достаточно использовать единственный вектор, индексированный именами вершин.

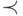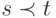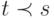Частичный порядок (partial order) есть транзитивное нерефлексивное отношение. Нетрудно доказать, что из нерефлексивности и транзитивности следует, что частичные порядки асимметричны: если и , то 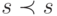(в силу транзитивности), а это противоречит нерефлексивности, т.е. невозможно одновременно 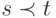и 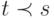. Продолжая эти рассуждения, можно показать, что частичный порядок не может содержать циклы, такие как 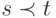, и . Ниже приведены примеры типичных частичных порядков:

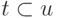Включение подмножеств. Отношение " включает, но не равно " (), определенное для подмножеств заданного множества, является частичным порядком — конечно, он не рефлексивен, и если и , то .

Пути в DAG-графах. Отношение " достижим по непустому пути из... " является частичным порядком на вершинах DAG-графа без петель, поскольку оно транзитивно и нерефлексивно. Подобно отношениям эквивалентности и неориентированным графам, этот конкретный частичный порядок важен для многих приложений, поскольку DAG — это сжатое неявное представление частичного порядка.

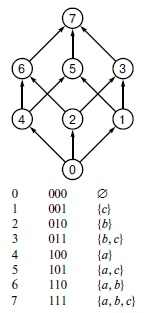
Например, на рис. 19.17 приведены DAG-графы частичных порядков включения подмножеств, количество ребер которых составляет лишь небольшую часть мощности частичного порядка (см. упражнение 19.73).

Рис. 19.17. DAG-граф включения множеств

В DAG-графе, показанном в верхней части рисунка, индексы вершин представляют подмножества множества из трех элементов, которые приведены в таблице в нижней части рисунка. Транзитивное замыкание этого графа представляет собой частичный порядок включения подмножеств: ориентированный путь между двумя узлами существует в том и только том случае, когда подмножество, представленное первым узлом, содержится в подмножестве, представленном вторым узлом.

Вообще-то частичные порядки редко определяются перечислением всех упорядоченных пар, поскольку таких пар очень много. Вместо этого обычно определяется нерефлексивное отношение (DAG) и рассматривается его транзитивное замыкание. Это и есть основная причина изучения реализаций АТД для абстрактных транзитивных замыканий DAG-графов. Работа с DAG-графами и примеры частичных порядков будут рассматриваться в разделе 19.5.

Полный порядок (total order) T — это частичный порядок, в котором для всех s Ф t выполняется либо sTt, либо tTs. Знакомыми нам примерами полного порядка являются отношение " меньше чем " на множествах целых или вещественных чисел или лексикографическое упорядочение строк символов. Наши алгоритмы сортировки и поиска в частях III и IV основываются на реализации АТД полного порядка множеств. В полном порядке существует один и только один способ упорядочить элементы множества так, чтобы выполнялось отношение sTt, если s предшествует t; а в частичном порядке, который не является полным, может быть много способов такого упорядочения. Алгоритмы решения этой задачи будут рассмотрены в разделе 19.5.

Резюмируя, можно сказать, что приведенные ниже соответствия между множествами и моделями графов помогают лучше понять, насколько важны фундаментальные алгоритмы на графах и как широко они применяются на практике:

• Отношения и орграфы.
• Симметричные отношения и неориентированные графы.
• Транзитивные отношения и пути в графах.
• Отношения эквивалентности и пути в неориентированных графах.
• Частичные порядки и пути в DAG-графах.

Этот список упорядочивает виды изучаемых нами графов и алгоритмов и является дополнительным стимулом изучения базовых свойств DAG-графов и алгоритмов их обработки.

Упражнения

19.67. Покажите, что отношение " имеет тот же остаток при делении на k " транзитивно (и, следовательно, является отношением эквивалентности) на множестве целых чисел.

19.68. Покажите, что отношение " в том же реберно-связном компоненте, что и... " является отношением эквивалентности на множестве вершин любого графа.

19.69. Покажите, что отношение " в том же двусвязном компоненте, что и. " не является отношением эквивалентности на множестве вершин любого графа.

19.70. Докажите, что транзитивное замыкание отношения эквивалентности также является отношением эквивалентности, и что транзитивное замыкание частичного порядка также является частичным порядком.

19.71. Мощность отношения — это количество его упорядоченных пар. Покажите, что мощность отношения эквивалентности равна сумме квадратов мощностей классов эквивалентности этого отношения.

19.72. Используя онлайновый словарь, постройте граф, который представляет отношение эквивалентности " имеет к общих букв с. " на множестве слов. Определите количество классов эквивалентности для к = 1, ..., 5.

19.73. Мощность частичного порядка равна количеству его упорядоченных пар. Какова мощность частичного порядка включения подмножеств для множества из n элементов?

19.74. Покажите, что частичный порядок " является делителем " представляет собой частичный порядок на множестве целых чисел.