Орграфы и DAG-графы

DAG -графы

В этом разделе мы рассмотрим различные приложения DAG-графов (directed acyclic graph — ориентированный ациклический граф). На то имеются две причины. Во-первых, они служат неявными моделями частичных порядков, и зачастую в приложениях мы имеем дело непосредственно с DAG-графами — поэтому нужны эффективные алгоритмы обработки таких графов. Во-вторых, такие приложения помогают лучше понять сущность DAG-графов, а понимание DAG-графов важно для понимания орграфов вообще.

Поскольку DAG-графы являются частным видом орграфов, все задачи обработки DAG-графов элементарно сводятся к задачам обработки орграфов. Естественно ожидать, что обрабатывать DAG-графы проще, чем обрабатывать орграфы общего вида, однако понятно, что если мы столкнемся с задачей, которая трудно решается на DAG-графе, то решение этой же задачи на орграфах общего вида вряд ли будет проще. Как мы увидим, задача вычисления транзитивного замыкания принадлежит как раз к этой категории. Оценка сложности обработки DAG-графов также важна, ведь каждый орграф содержит коренной DAG (см. лемму 19.2), т.е. DAG-графы встречаются даже при работе с орграфами, не являющимися DAG-графами.

Классическое приложение, в котором непосредственно возникают DAG-графы, называется составлением расписания (scheduling). В общем случае решение задачи составления расписаний заключается в организации выполнения некоторого множества задач (task) при наличии множества ограничений (constraint) т.е. в указании, когда и как должны выполняться эти задачи. Ограничениями могут быть некоторые функции от времени выполнения или от других ресурсов, потребляемых задачами. Наиболее важный вид ограничений — ограничения предшествования (precedence constraints), которые определяют, что одни задачи должны быть обязательно выполнены перед выполнением других задач, т.е. задают на множестве задач частичный порядок. Различные виды дополнительных ограничений порождают различные виды задач составления расписаний разной степени сложности. Изучены уже буквально тысячи различных задач, и для многих из них исследователи продолжают поиск более совершенных алгоритмов.

Возможно, простейшую нетривиальную задачу составления расписания можно сформулировать следующим образом:

Составление расписаний. Пусть дано множество задач, требующих выполнения, и частичный порядок, определяющий, что решение некоторых задач должно быть завершено прежде, чем начнется выполнение некоторых других задач. Как составить график выполнения задач, чтобы выполнить их все с учетом частичного порядка?

В этом базовом виде задача составления расписания называется топологической сортировкой (topological sorting). Ее решение несложно, и в следующем разделе мы рассмотрим два алгоритма. В более сложных практических приложениях могут понадобиться дополнительные ограничения на планирование выполнения задач, и тогда задача усложняется. Например, задачи могут соответствовать курсам лекций в расписании занятий студентов, а частичный порядок может определяться требованиями подготовки к каждому курсу. Топологическая сортировка способна найти расписание занятий, удовлетворяющее требованиям подготовки, но она может не справиться с другими видами ограничений, которые бывает нужно добавить в модель: конфликты курсов, ограничения на количество слушателей курса и т.д. Еще один пример: задачи могут быть частями некоторого производственного процесса, а частичный порядок может задавать цепочки конкретных процессов. Топологическая сортировка позволяет планировать задачи, но, возможно, существует другой способ, требующий меньше времени, денег или других ресурсов, не учтенных в модели. Различные варианты задачи составления расписаний, которые учитывают подобные более общие ситуации, будут рассмотрены в "Кратчайшие пути" и "Потоки в сетях" .

Часто сначала нужно проверить, действительно ли заданный DAG-граф не содержит направленных циклов. Как было показано в 19.2, нетрудно реализовать класс, который позволяет клиентам проверять за линейное время, является ли орграф общего типа DAG-графом — для этого нужно выполнить стандартный поиск в глубину и проверить, что в лесе DFS нет обратных ребер (см. упражнение 19.75). Для реализации алгоритмов обработки DAG-графов мы реализуем специальные клиентские классы нашего стандартного АТД GRAPH, которые предназначены для обработки орграфов без циклов, а проверку отсутствия циклов должны выполнять клиентские программы. При этом возможно, что алгоритм обработки DAG-графов выдаст полезные результаты, даже если запустить его на орграфе с циклами, и иногда это бывает нужно. Разделы 19.6 и 19.7 посвящены реализациям классов топологической сортировки (DAGts) и классов определения достижимости в DAG-графах (DAGts и DAGreach); программа 19.13 представляет собой пример клиента такого класса.

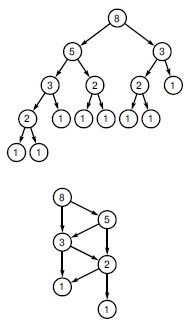
В некотором смысле DAG — это частично дерево и частично граф. Конечно, мы воспользуемся этими особенностями структуры для их обработки. Например, при желании можно рассматривать DAG как дерево. Предположим, что необходимо выполнить обход вершин DAG-графа D, как будто это дерево с корнем в вершине w — чтобы, например, результат обхода двух DAG-графов на рис. 19.18 рис. 19.18 с помощью этой программы был одним и тем же. Следующая простая программа выполняет эту задачу так же, как это сделал бы рекурсивный обход дерева:

  void traverseR(Dag D, int v)
    { visit(v);
      typename Dag::adjIterator A(D, v);
      for (int t = A.beg(); !A.end(); t = A.nxt())
        traverseR(D, t);
    }
      

Однако мы редко будем выполнять подобный полный обход, поскольку обычно будем пользоваться преимуществами DAG-графов, которые позволяют экономить память и время при их обходе (например, пометка посещенных вершин при обычном поиске в глубину). Та же идея применяется и к поиску, где рекурсивный вызов выполняется только для одной ссылки, инцидентной каждой вершине. В таком алгоритме затраты на поиск в DAG-графе и дереве оказываются одними и теми же, но DAG использует гораздо меньше памяти.

Поскольку DAG-графы обеспечивают компактное представление деревьев, в которых имеются идентичные поддеревья, мы часто используем их вместо деревьев для представления различных вычислительных абстракций. В контексте построения алгоритмов различия между представлением выполнения программы в виде DAG являются существенным компонентом динамического программирования (см., например, рис. 19.18 и упражнение 19.78). Кроме того, DAG-графы широко используются в компиляторах в качестве промежуточных представлений арифметических выражений и программ (см., например, рис. 19.19) и в системах проектирования электронных схем в качестве промежуточных представлений комбинационных элементов.

Рис. 19.18. Модель DAG вычислений чисел Фибоначчи

Дерево в верхней части описывает зависимость вычисления очередного числа от вычисления двух его предшественников. DAG-граф в нижней части демонстрирует ту же зависимость, хотя использует лишь часть узлов.

При работе с бинарными деревьями часто возникает важная ситуация. На DAG-графы можно наложить те же ограничения, что и на деревья при определении бинарных деревьев.

Рис. 19.19. Представление арифметического выражение с помощью DAG-графа

Оба изображенных здесь DAG-графа являются представлениями одного и того же арифметического выражения (c*(a+b))-((a+b)*(a+b)+e)). В бинарном дереве грамматического разбора (слева) листы представляют операнды, а все внутренние узлы — операции, выполняемые над выражениями, представленными двумя их поддеревьями (см. рис. 5.31). DAG-граф в правой части — это более компактное представление того же дерева. Важно то, что значение выражения можно вычислить за время, пропорциональное размеру DAG, который обычно значительно меньше, чем размер дерева (см. упражнения 19.112 и 19.113).

Различие между бинарными DAG-графами и бинарными деревьями заключается в том, что в бинарном DAG на конкретный узел может указывать более чем одна ссылка. Как и наше определение бинарных деревьев, это определение моделирует естественное представление, где каждый узел представляет собой структуру с левой ссылкой и с правой ссылкой, которые указывают на другие узлы (либо пусты), и действует лишь глобальное ограничение: не разрешены направленные циклы. Бинарные DAG-графы имеют большое значение, поскольку они обеспечивают компактный способ представления бинарных деревьев в некоторых приложениях. Например, как показано на рис. 19.20 и в программе 19.5, trie-дерево существования можно сжать до бинарного DAG без изменения реализации поиска.

Рис. 19.20. Сжатие бинарного дерева

Таблица из девяти пар целых чисел в левой части рисунка является компактным представлением бинарного DAG (внизу справа), который представляет собой сжатую версию бинарного дерева, показанного вверху. В этой структуре данных метки узлов не хранятся в явном виде: таблица представляет восемнадцать ребер 1-0, 1-0, 2-1, 2-1, 3-1, 3-2 и т.д., однако содержит только конечные вершины левых и правых ребер каждого узла (как в бинарном дереве), а их начальные вершины неявно задаются индексом таблицы.

Алгоритм, который зависит только от формы дерева, эффективно работает и на DAG-графах. Пусть, например, дерево является trie-деревом существования для двоичных ключей, соответствующих листовым узлам, т.е. оно представляет ключи 0000, 0001, 0010, 0110, 1100 и 1101.

Успешный поиск ключа 1101 проходит вправо, вправо, влево и вправо, и завершается в листовом узле. В DAG-графе такой же поиск шел бы от 9 через 8, 7 и 2 в 1.

Эквивалентный вариант — рассматривать ключи trie-дерева как соответствующие строкам в таблице истинности булевской функции, для которых эта функция возвращает истинное значение (см. упражнения 18.84—18.87). Бинарный DAG есть модель экономичной схемы, которая вычисляет эту функцию. В таком приложении бинарные DAG-графы называются деревьями решений (binary decision diagram — BDD).

Программа 19.5. Представление бинарного дерева в виде бинарного DAG-графа

Этот кодовый фрагмент реализует обратный обход, который выполняет построение бинарного DAG, соответствующего структуре бинарного дерева (см. главу 12 "Таблицы символов и деревья бинарного поиска" ), выявляя общие поддеревья. В нем применяется класс индексирования наподобие ST из программы 17.15 (измененный для работы с парами целых чисел, а не строковых ключей), чтобы присваивать уникальные целочисленные значения каждой отдельной древовидной структуре и применять их в представлении DAG вектором структур из двух целых чисел (см. рис. 19.20 рис. 19.20). Пустому дереву (пустая ссылка) присваивается индекс 0 , дереву с единственным узлом (и с двумя пустыми ссылками) — индекс 1 и т.д.

Индекс, соответствующий каждому поддереву, вычисляется рекурсивно. Затем создается ключ — такой, что каждый узел с такими же поддеревьями будет иметь тот же индекс, и этот индекс возвращается после заполнения ссылок ребра (поддерева) DAG-графа.

  int compressR(link h)
    { STx st;
      if (h == NULL) return 0;
      l = compressR(h->l);
      r = compressR(h->r);
      t = st. index(l, r) ;
      adj[t].l = l; adj[t].r = r;
      return t;
    }
      

В двух последующих разделах мы начнем изучение алгоритмов обработки DAG-графов. Эти алгоритмы не только приводят к реализациям эффективных и полезных функций АТД для DAG-графов, но и позволяют оценить сложность обработки орграфов. Но мы увидим и то, что хотя DAG-графы значительно проще орграфов общего вида, некоторые фундаментальные задачи решить для них нисколько не проще.

Упражнения

19.75. Реализуйте класс DFS, который может использоваться клиентами для проверки, что DAG-граф не содержит циклов.

19.76. Напишите программу, которая генерирует случайные DAG-графы: для этого она строит случайные орграфы, выполняет поиск в глубину из случайной исходной точки и отбрасывает обратные ребра (см. упражнение 19.40). Экспериментально определите параметры программы для получения DAG-графов с приблизительно E ребрами при заданном V.

19.77. Сколько узлов содержит дерево и DAG-граф, соответствующие рис. 19.18, для вычисления N-го числа Фибоначчи (F_N)?

19.78. Приведите DAG-граф, соответствующий примеру динамического программирования, для модели задачи о ранце из "Рекурсия и деревья" (см. рис. 5.17).

19.79. Разработайте АТД для бинарных DAG-графов.

19.80. Можно ли любой DAG представить в виде бинарного DAG (см. лемму 5.4)?

19.81. Напишите функцию, которая выполняет поперечный обход бинарного DAG-графа с одним источником. То есть эта функция должна посетить все вершины, которые можно достичь через левое ребро, затем посетить исходную вершину, а потом посетить все вершины, которые можно достичь через правое ребро.

19.82. В стиле рис. 19.20 нарисуйте trie-дерево существования и соответствующий бинарный DAG для ключей 01001010 10010101 00100001 11101100 01010001 00100001 00000111 01010011.

19.83. Реализуйте АТД, основанный на построении trie-дерева существования из набора 32-битовых ключей, сжатии его до бинарного DAG и использовании этой структуры данных для ответов на запросы о существовании.

19.84. Начертите дерево решений для таблицы истинности функции от четырех переменных, которая возвращает 1 тогда и только тогда, когда количество переменных, равных 1, нечетно.

19.85. Напишите функцию, которая принимает в качестве аргумента 2ⁿ-разрядную таблицу истинности и возвращает соответствующее дерево решений. Например, для аргумента 1110001000001100 программа должна вернуть представление бинарного DAG-графа с рис. 19.20.

19.86. Напишите функцию, которая принимает в качестве аргумента 2ⁿ таблицу истинности, вычисляет все перестановки аргументов и, пользуясь решением упражнения 19.85, возвращает перестановку, которая приводит к наименьшему дереву решений.

19.87. Эмпирически определите эффективность стратегии из упражнения 19.85 для различных булевых функций, как стандартных, так и случайно сгенерированных.

19.88. Напишите программу, аналогичную программе 19.5, которая поддерживает удаление общих подвыражений: для заданного бинарного дерева, представляющего арифметическое выражение, нужно вычислить бинарный DAG-граф, представляющий то же выражение, из которого удалены общие подвыражения.

19.89. Начертите все неизоморфные DAG-графы с двумя, тремя, четырьмя и пятью вершинами.

19.90. Сколько существует различных DAG-графов с Vвершинами E ребрами?

19.91. Сколько существует различных DAG-графов с Vвершинами E ребрами, если считать два DAG различными только если они не изоморфны?