Орграфы и DAG-графы

Анатомия DFS в орграфах

Код DFS для неориентированных графов из "Поиск на графе" можно использовать для посещения каждого ребра и каждой вершины орграфа. Основной принцип этого рекурсивного алгоритма остается прежним: чтобы посетить каждую вершину, достижимую из данной вершины, мы помечаем эту вершину как посещенную, а затем (рекурсивно) посещаем все вершины, в которые можно попасть из каждой вершины, находящейся в ее списке смежности.

В неориентированных графах имеются два представления каждого ребра, но второе представление, которое встречается при поиске в глубину, всегда приводит в помеченную вершину и поэтому игнорируется (см. "Поиск на графе" ). В орграфе имеется только одно представление каждого ребра, поэтому можно было бы надеяться на упрощение алгоритмов DFS в орграфах. Однако орграфы сами являются более сложными комбинаторными объектами, так что эти надежды не оправдываются. Например, деревья поиска, которые мы используем для понимания функционирования алгоритма, имеют в случае орграфов более сложную структуру, чем для неориентированных графов. И это усложняет разработку алгоритмов для работы с орграфами. Как мы вскоре убедимся, сделать какие-то выводы об ориентированных путях в орграфах гораздо труднее, чем о путях в неориентированных графах.

Как и в "Поиск на графе" , мы воспользуемся двумя терминами. Термин стандартный поиск в глубину по спискам смежности (standard adjacency-lists DFS) будет обозначать процесс вставки последовательности ребер в АТД орграфа, представленного списками смежности (второй аргумент конструктора из программы 17.9 имеет значение true), с последующим выполнением поиска в глубину — например, с помощью программы 18.3. Параллельный термин стандартный поиск в глубину по матрице смежности (standard adjacency-matrix DFS) будет обозначать процесс вставки последовательности ребер в АТД орграфа, представленного матрицей смежности (второй аргумент конструктора из программы 17.7 имеет значение true), с последующим выполнением поиска в глубину — например, с помощью той же программы 18.3.

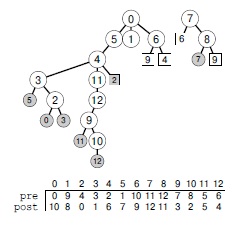
К примеру, на рис. 19.9 показано дерево рекурсивных вызовов, которое описывает выполнение алгоритма стандартного поиска в глубину по спискам смежности для орграфа с рис. 19.1. Как и в случае неориентированных графов, подобные деревья содержат внутренние узлы, которые соответствуют вызовам рекурсивной функции DFS для каждой вершины, при этом ссылки на внешние узлы соответствуют ребрам, которые ведут в уже просмотренные вершины. Классификация узлов и связей дает информацию о поиске (и о самом орграфе), однако такая классификация для орграфов существенно отличается от классификации для неориентированных графов.

Рис. 19.9. Лес DFS для орграфов

Данный лес описывает стандартный поиск в глубину по спискам смежности орграфа с рис. 19.1. Внешние узлы представляют уже посещенные внутренние узлы с теми же метками; во всем остальном этот лес является представлением орграфа, где все ребра направлены вниз. Существуют четыре типа ребер: (1) древесные ребра, ведущие во внутренние узлы; (2) обратные ребра, ведущие во внешние узлы, которые представляют предшественников (серые кружки); (3) нисходящие ребра, ведущие во внешние узлы, которые представляют потомков (серые квадратики); и (4) поперечные ребра, ведущие во внешние узлы, не являющиеся ни предшественниками, ни потомками (светлые квадратики). Тип ребер, ведущих в посещенные узлы, можно определить, сравнивая прямые и обратные номера их начальных и конечных узлов (внизу):

Например, ребро 7-6 является поперечным, поскольку и прямой, и обратный номера узла 7 больше, чем аналогичные номера узла 6 .

В неориентированных графах каждая ссылка в дереве DFS относится к одному из четырех классов. Это зависит от того, соответствует ли она ребру графа, которое ведет к рекурсивному вызову, и соответствует ли она первому или второму представлению ребра, встреченному алгоритмом поиска.

В орграфах имеется взаимно однозначное соответствие между ссылками дерева и ребрами графа, которые попадают в один из четырех различных классов:

• Ребра, представляющие рекурсивный вызов (древесные (tree) ребра).
• Ребра, ведущие из вершины к предку в ее дереве DFS (обратные (back) ребра).
• Ребра, ведущие из вершины к потомку в ее дереве DFS (нисходящие (down) ребра).
• Ребра, ведущие из одной вершины в другую, не являющуюся ни предшественником, ни потомком в ее дереве DFS (поперечные (cross) ребра).

Древесные ребра ведут в непосещенные вершины и соответствуют рекурсивному вызову при поиске в глубину. Обратные, поперечные и нисходящие ребра ведут в посещенные вершины. Чтобы определить тип заданного ребра, мы используем прямую и обратную нумерацию (очередность посещения узлов, соответственно, при прямом и обратном обходе леса).

Программа 19.2 представляет собой класс DFS, который определяет вид каждого ребра орграфа, а на рис. 19.10 приведен пример ее работы для орграфа с рис. 19.1. Во время поиска проверка, ведет ли какое-либо ребро в узел с большим обратным номером, эквивалентна проверке, присвоен ли уже обратный номер. Любой узел, которому уже присвоен прямой номер, но еще не присвоен обратный номер, является предком в дереве DFS и поэтому его обратный номер больше обратного номера текущего узла.

Рис. 19.10. Трассировка орграфа поиска в глубину

Здесь приведены выходные результаты программы 19.2 для орграфа с рис. 19.1. Они в точности соответствуют прямому обходу дерева DFS, показанному на рис. 19.9.

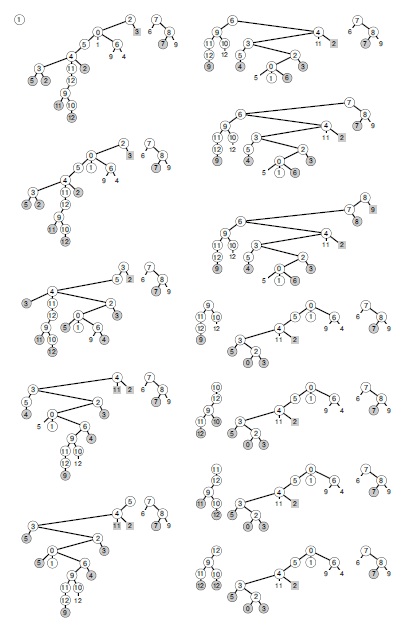
Как было сказано в "Виды графов и их свойства" для неориентированных графов, виды ребер зависят скорее от динамики поиска, чем от самого графа. Различные леса DFS для одного и того же графа могут существенно различаться по характеру (см. рис. 19.11). Даже количество деревьев леса DFS может зависеть от начальной вершины.

Однако несмотря на все эти различия, некоторые классические алгоритмы обработки орграфов способны определить свойства орграфов, выполняя соответствующие действия при встрече различных видов ребер во время поиска в глубину.

Рис. 19.11. Лес DFS на орграфе

Эти леса описывают поиск в глубину на том же графе, что и на рис. 19.9, где функция поиска на графе проверяет вершины (и вызывает рекурсивную функцию для непосещен-ных вершин) в порядке s, s + 1, ..., V-1, 0, 1, ... , s-1 для каждого s. Структура леса определяется как динамикой поиска, так и структурой самого графа. У каждого узла одни и те же дочерние узлы (узлы в его списке смежности в порядке их следования) в любом лесу. Крайнее левое дерево в каждом лесу содержит все узлы, достижимые из его корня, однако выводы о достижимости из других вершин усложняются из-за наличия обратных, поперечных и нисходящих ребер. Даже количество деревьев в лесе зависит от выбора начальной вершины, поэтому нет прямого соответствия между деревьями в лесе и сильными компонентами, как в неориентированных графах. Например, в данном случае все вершины достижимы из вершины 8 , только если начать поиск из вершины 8.

Программа 19.2. DFS на орграфе

Данный класс DFS использует прямую и обратную нумерацию, чтобы показать роль каждого ребра графа в поиске в глубину (см. рис. 19.10).

  template <class Graph>
  class DFS
    { const Graph &G;
      int depth, cnt, cntP;
      vector<int> pre, post;
      void show(char *s, Edge e)
        { for (int i = 0; i < depth; i++) 
        cout << " ";
          cout << e.v << "-" << e.w << s << endl;
        }
      void dfsR(Edge e)
        { int w = e.w; show(" древесное", e);
          pre[w] = cnt++; depth++;
          typename Graph::adjIterator A(G, w);
          for (int t = A.beg(); !A.end(); t = A.nxt())
            { Edge x( w, t) ;
              if (pre[t] == -1) dfsR(x);
              else if (post[t] == -1) show(" обратное", x);
              else if (pre[t] > pre[w]) show(" нисходящее", x);
              else show(" поперечное", x);
            }
          post[w] = cntP++; depth--;
        }
    public:
      DFS(const Graph &G) : G(G), cnt(0), cntP(0),
        pre(G.V(), -1), post(G.V(), -1)
        { for (int v = 0; v < G.V(); v++)
            if (pre[v] == -1) dfsR(Edge(v, v));
        }
    };