Орграфы и DAG-графы

Например, рассмотрим следующую фундаментальную задачу.

Обнаружение направленного цикла. Содержит ли заданный орграф направленные циклы? (Является ли он DAG-графом?) В неориентированных графах любое ребро, ведущее в посещенную вершину, означает наличие цикла; но в орграфах следует обращать внимание только на обратные ребра.

Любой орграф можно преобразовать в DAG, выполнив поиск в глубину и удалив все ребра графа, которые соответствуют обратным ребрам в DFS. Например, из рис. 19.9 рис. 19.9 видно, что удаление ребер 2-0, 3-5, 2-3, 9-11, 10-12, 4-2 и 7-8 преобразовывает орграф с рис 19.1 в DAG-граф. Конкретный вид полученного DAG-графа зависит от представления исходного графа и от динамических свойств поиска в глубину (см. упражнение 19.37). Этот метод представляет собой удобный способ генерации больших случайных DAG-графов (см. упражнение 19.76) для тестирования алгоритмов обработки DAG-графов.

Сравнение только что описанного решения с решением, приведенным в "Поиск на графе" для неориентированных графов, дает основание трактовать эти два вида графов как различные комбинаторные объекты, даже если их представления подобны, а некоторые программы работают для обоих видов. Судя по нашим определениям, мы вроде бы используем для решения этой задачи тот же метод, что и для обнаружения циклов в неориентированных графах (поиск обратных ребер), однако наша реализация для неориентированных графов на орграфе работать не будет. Например, в "Поиск на графе" мы внимательно подходили к различиям между родительскими ссылками и обратными ссылками, поскольку существование родительской ссылки не означает наличия цикла (циклы в неориентированных графах должны содержать не меньше трех вершин). Однако нельзя игнорировать обратные ссылки на родительские узлы в орграфах, ведь пары вершин со взаимными ссылками в орграфах считаются циклами. В принципе, можно было бы определить обратные ребра в неориентированных графах так же, как и здесь, однако тогда потребовалось бы явное исключение для случая с двумя вершинами. Хотя более важно то, что в неориентированных графах мы можем обнаруживать циклы за время, пропорциональное V (см. "Поиск на графе" ), однако для обнаружения цикла в орграфе может понадобиться время, пропорциональное E (см. упражнение 19.32).

По существу, DFS — это систематический способ посещения всех вершин и всех ребер графа. То есть он дает фундаментальный подход к решению задачи достижимости в орграфах, хотя эта задача и сложнее, чем для неориентированных графов.

Достижимость из одного истока. До каких вершин заданного орграфа можно добраться из заданной начальной вершины s? Сколько имеется таких вершин?

Рис. 19.12. Декомпозиция орграфа

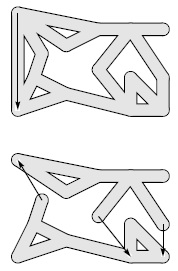
Доказательство методом индукции того, что поиск в глубину приводит нас во все места орграфа, достижимые из заданного узла, по существу ничем не отличается от доказательства для метода Тремо. Здесь приведен пример в виде лабиринта (вверху), аналогичный рис. 18.4. Мы разбиваем граф на две меньшие части (внизу), индуцированные двумя множествами вершин: вершинами, которые могут быть достигнуты, если пройти по первому ребру из начальной вершины без ее дальнейшего посещения (нижняя часть), и вершинами, которые остаются недостижимыми, если пройти по первому ребру и не возвращаться в исходную вершину (верхняя часть). Любое ребро, исходящее из вершины первого множества в исходную вершину, пропускается во время поиска, т.к. исходная вершина уже помечена. Любое ребро, исходящее из вершины второго множества в какую-либо вершину первого множества, пропускается потому, что все вершины первого множества помечены еще до начала поиска во втором подграфе.

В отличие от неориентированных графов, DFS на орграфе не дает полной информации о достижимости из любой вершины, кроме исходной, поскольку ребра дерева являются ориентированными, а поисковые структуры содержат поперечные ребра. Когда мы уходим из какой-либо вершины вниз по дереву, мы не можем быть уверены в том, что существует обратный путь в эту вершину по ребрам орграфа; и в общем случае такого пути действительно нет. Например, после выбора древесного ребра дерева 4-11 уже невозможно вернуться в вершину 4. А при игнорировании поперечных и обратных ребер (поскольку они ведут в уже посещенные вершины) игнорируется и вся связанная с ними информация (множество вершин, достижимых из конечной вершины). Например, проход по ребру 6-9 на рис. 19.9 — единственный способ обнаружить, что вершины 10, 11 и 12 достижимы из вершины 6.

Чтобы определить вершины, достижимые из другой вершины, видимо, нужно выполнить новый поиск в глубину из этой вершины (см. рис. 19.11). Можно ли воспользоваться информацией из предыдущих поисков, чтобы повысить эффективность этого процесса? Мы рассмотрим подобные вопросы в разделе 19.7.

При определении связности в неориентированных графах используется тот факт, что вершины соединены со своими предками в дереве DFS посредством (по крайней мере) пути в этом дереве. Однако в орграфах все не так: ориентированный путь из вершины орграфа к ее предку существует только в том случае, если существует обратное ребро из какого-либо ее потомка к этому или еще более дальнему предку. Далее, связность в неориентированных графах для каждой вершины полностью описывается деревом DFS с корнем в этой вершине; а в орграфах поперечные ребра могут увести нас в любую уже посещенную часть поисковой структуры, даже в другое дерево леса DFS. В неориентированных графах мы могли воспользоваться этим свойством связности, чтобы ассоциировать каждую вершину с каким-либо связным компонентом за один проход DFS, а затем использовать эту информацию для определения за постоянное время, являются ли любые две вершины связными. В случае орграфа, как мы уже смогли убедиться в этой главе, все не так легко.

В этой и в предыдущей главах мы видели, что различные способы выбора непосе-щенных вершин приводят к различным динамикам DFS. В случае орграфов структурная сложность деревьев DFS приводит к различиям в динамике поиска, которые еще ярче выражены, чем в неориентированных графах. Например, на рис. 19.11 продемонстрированы существенные различия для орграфов даже просто при изменении порядка просмотра вершин высокоуровневыми функциями. На этом рисунке приведена лишь мизерная часть таких возможностей — ведь в принципе каждый из V! различных порядков просмотра вершин может приводить к различным результатам. В разделе 19.7 мы рассмотрим один важный алгоритм, в котором учитывается эта гибкость, и непосе-щенные вершины обрабатываются на верхнем уровне (корни деревьев DFS) в особом порядке, который сразу же выявляет сильные компоненты.

Упражнения

19.30. Начертите лес DFS, который получается при выполнении поиска в глубину на орграфе

3-71-47-80-55-23-82-90-64-92-66-4,представленно мспискамисмежно сти.

19.31. Начертите лес DFS, который получается при выполнении поиска в глубину на орграфе

3-71-47-80-55-23-82-90-64-92-66-4,представленно мматрицейсмежно сти.

19.32. Опишите семейство орграфов с Vвершинами и E ребрами, для которых стандартный поиск в глубину по спискам смежности находит циклы за время, пропорциональное E.

19.33. Покажите, что при работе DFS на орграфе никакое ребро не соединяет какой-либо узел с другим узлом, прямой и обратный номера которого меньше соответствующих номеров первого узла.

19.34. Покажите все возможные леса DFS для орграфа

0-10-20-31-32-3,

и сведите в таблицу количество древесных, обратных, поперечных и нисходящих ребер для каждого леса.

19.35. Если обозначить количества древесных, обратных, поперечных и нисходящих ребер, соответственно, через t, b, с и d, то для любого поиска в глубину на любом орграфе с V вершинами и E ребрами будут верны соотношения t + b + с + t = E и t < V. Какие другие соотношения между этими переменными можно обнаружить? Какие из этих значений зависят только от свойств графов, а какие — от динамических свойств DFS?

19.36. Докажите, что каждый исток в орграфе должен быть корнем некоторого дерева в лесе, соответствующем любому поиску в глубину на этом орграфе.

19.37. Постройте связный DAG-граф, удалив в графе, который изображен на рис. 19.1, пять ребер (см. р рис. 19.11).

19.38. Реализуйте класс орграфа, который предоставляет клиенту возможность проверять, что заданный орграф на самом деле является DAG-графом, и напишите реализацию на основе DFS.

19.39. Воспользуйтесь решением из упражнения 19.38 для (эмпирической) оценки вероятности того, что случайный орграф с Vвершинами и E ребрами представляет собой DAG, для различных видов орграфов (см. упражнения 19.11—19.18).

19.40. Эмпирически определите относительное процентное содержание древесных, обратных, поперечных и нисходящих ребер при выполнении поиска в глубину на различных видах орграфов (см. упражнения 19.11—19.18).

19.41. Опишите, как построить последовательность ориентированных ребер между V вершинами, для которых при стандартном поиске в глубину на представлении списками смежности не будет ни поперечных, ни нисходящих ребер, а количество обратных ребер пропорционально V².

19.42. Опишите, как построить последовательность ориентированных ребер V вершин, для которых при стандартном поиске в глубину на представлении списками смежности не будет ни обратных, ни нисходящих ребер, а количество поперечных ребер пропорционально V².

19.43. Опишите, как построить последовательность ориентированных ребер V вершин, для которых при стандартном поиске в глубину на представлении списками смежности не будет ни обратных, ни поперечных ребер, а количество нисходящих ребер пропорционально V².

19.44. Приведите правила, соответствующие обходу методом Тремо лабиринта, в котором все коридоры являются односторонними.

19.45. Добавьте в решения, полученные в упражнениях 17.56—17.60, возможность вывода стрелок на ребрах (в качестве примеров используйте рисунки из данной главы).