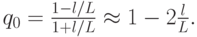Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
6.2.2. Метод простых итераций с оптимальным параметром
Представим сеточную функцию невязки 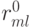 , равную нулю на границе, в виде разложения по базису из собственных функций разностного оператора (
, равную нулю на границе, в виде разложения по базису из собственных функций разностного оператора (  — собственные функции оператора
— собственные функции оператора  )
)
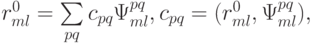
при этом выполняется равенство Парсеваля

Далее, используя это разложение, получим

Здесь используется то, что  являются собственными числами оператора
являются собственными числами оператора  . При сложении равенств
. При сложении равенств  и
и 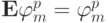 получаем
получаем  . Легко получается оценка нормы этой сеточной функции на первой итерации:
. Легко получается оценка нормы этой сеточной функции на первой итерации:
![\left\| {v^1}\right\| = \sqrt{\sum {c_{pq}^2 (1 - \tau {\lambda}^{pq})^2}} \le \max\limits_{{\lambda}\in [l, L]} \left| {1 -{\tau}{\lambda}}\right| \sqrt{\sum {c_{pq}^2}} = \max\limits_{{\lambda}\in [l, L]} \left| {1 -{\tau}{\lambda}}\right| \left\| {{\mathbf{R}}^0}\right\|.](/sites/default/files/tex_cache/8ccad3d9624c4eac26088cfcabf0bc00.png)
Для последовательности итераций также легко получается стандартная оценка нормы
![\left\| {{\mathbf{r}}^{i}}\right\| \le (\max\limits_{{\lambda}\in [l, L]} \left| {1 -{\tau}{\lambda}}\right|)^{i} \left\| {{\mathbf{r}}^{0}}\right\|.](/sites/default/files/tex_cache/ae2ceac28b4d1c5384e8eae3ebfab44a.png)
Отсюда видно, что значение q вычисляется, как  , а условие сходимости q < 1 выполняется при
, а условие сходимости q < 1 выполняется при  . Границы спектра разностного оператора уже оценены в предыдущем пункте.
. Границы спектра разностного оператора уже оценены в предыдущем пункте.
Для определения параметра 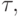 обеспечивающего максимальную
скорость сходимости, необходимо решать следующую оптимизационную задачу:
обеспечивающего максимальную
скорость сходимости, необходимо решать следующую оптимизационную задачу:
![\min\limits_{\tau} (\max\limits_{{\lambda} \in [l, L]} \left|{1 -{\tau}{\lambda}}\right|).](/sites/default/files/tex_cache/9f719f2210b1f7dc4fcb0c0356000bd3.png)
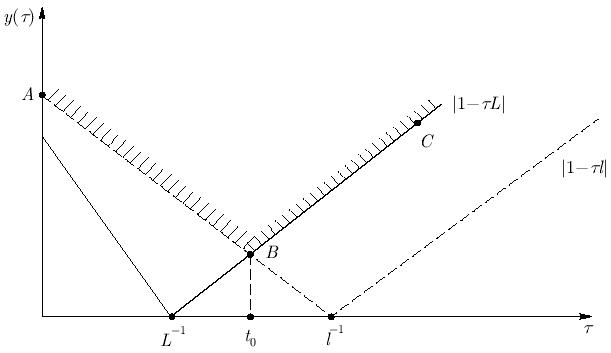
Так как 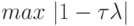 достигается на правой или левой границе интервала [l, L], то выполняется равенство
достигается на правой или левой границе интервала [l, L], то выполняется равенство ![\max\limits_{{\lambda}\in [l, L]} \left| {1 -{\tau}{\lambda}}\right| = \max \{\left| {1 -{\tau}l}\right|, \left| {1 -{\tau}L}\right| \}](/sites/default/files/tex_cache/75c8ba78e7a6a6c3fbf31659fd1dba9d.png) . В таком случае необходимо определить
. В таком случае необходимо определить 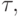 при котором достигается
при котором достигается  , или
, или ![\tau_0 = \arg [\min\limits_{\tau}\max (\left| {1 - \tau l}\right|, \left| {1 -{\tau}L}\right|)]](/sites/default/files/tex_cache/1d315c0edaa2470bcaa056910f5d8bb7.png) . где
. где 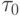 — оптимальный итерационный параметр.
— оптимальный итерационный параметр.
Как показано на рис. 6.1,  достигается при
достигается при  . Справа от точки B при любых
. Справа от точки B при любых  максимальна функция
максимальна функция  , слева — функция
, слева — функция  , и тогда минимум от искомого максимума достигается в точке B. Отсюда получим
, и тогда минимум от искомого максимума достигается в точке B. Отсюда получим 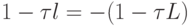 . Следовательно, значение оптимального итерационного параметра
. Следовательно, значение оптимального итерационного параметра 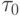 равно
равно
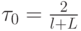
Оптимальное значение функции, отвечающей за скорость сходимости, будет
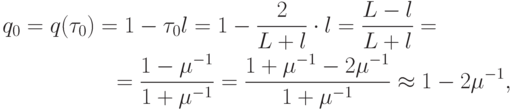
где  — число обусловленности системы сеточных уравнений.
— число обусловленности системы сеточных уравнений.
Количество итераций, соответствующее этому методу, легко оценивается:
![$ i = \left[{\frac{{\ln {\varepsilon}}}{{\ln q}}}\right] + 1 = \left[{\frac{{\ln {\varepsilon}}}{{\ln (1 - 2l/L)}}}\right] + 1 \approx \left[\frac{\ln {\varepsilon}}{(- 2l/L)} + 1 \approx \frac{L}{2l} \ln {\varepsilon}^{- 1} + 1\right]. $](/sites/default/files/tex_cache/4412c2a6391337fc8a679ad4e312cd89.png)
Пусть расчеты приводятся с точностью 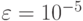 на сетке 100 x 100, тогда оценка числа итераций дает при
на сетке 100 x 100, тогда оценка числа итераций дает при  и L = 8N2
и L = 8N2

Показатель сходимости 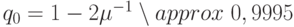 .
.
Параметр  — число обусловленности матрицы; чем оно больше, тем медленнее сходятся итерации. Напомним, что в n - мерном линейном нормированном пространстве Ln вводятся три наиболее употребительных нормы вектора:
— число обусловленности матрицы; чем оно больше, тем медленнее сходятся итерации. Напомним, что в n - мерном линейном нормированном пространстве Ln вводятся три наиболее употребительных нормы вектора:

которым, в соответствии с определением согласованной нормы матрицы 

сопоставляются нормы матрицы  с элементами aij:
с элементами aij:
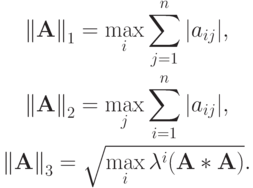
Показывается, что для симметричной матрицы  число обусловленности
число обусловленности  может быть представлено в третьей норме:
может быть представлено в третьей норме:

Таким образом, доказана следующая теорема.
Теорема.Рассмотрим итерационный метод 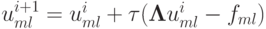 , с оператором
, с оператором  для численного решения разностного аналога уравнения Пуассона
для численного решения разностного аналога уравнения Пуассона

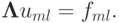
Пусть l и L — минимальное и максимальное
собственные числа оператора  соответственно.
соответственно.
Если итерационный параметр  удовлетворяет условию
удовлетворяет условию  , то последовательность итераций ui сходится к проекции решения исходного дифференциального уравнения, причем выполнено неравенство
, то последовательность итераций ui сходится к проекции решения исходного дифференциального уравнения, причем выполнено неравенство 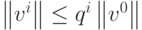 , где параметр 0 < q < 1 определяется следующим образом:
, где параметр 0 < q < 1 определяется следующим образом:
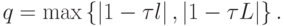
Параметр q принимает наименьшее значение q0 при

При этом