НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 6: Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Лемма 1.Пусть сеточная функция u_ml определена на сетке (x_m, y_l) (m, l = 0, ... , M) и во всех внутренних узлах сетки удовлетворяет уравнению

$\frac{{u_{{m} - 1, l} - 2u_{ml} + u_{m + 1, l}}}{{h^2}} + \frac{{u_{m, l - 1} - 2u_{ml} + u_{m, l + 1}}}{h^2} = f_{ml},$

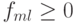причем во всех внутренних узлах сетки правая часть этого уравнения неотрицательная: ${f_{ml} \ge 0}$ . Тогда наибольшее значение сеточная функция u_ml достигает хотя бы в одной точке границы сеточной области.

Доказательство.

Предположим, что существует такая внутренняя точка области, в которой сеточная функция принимает наибольшее значение. Пусть это точка с индексами i, j. Перепишем разностное уравнение, несколько перегруппировав члены в левой части:

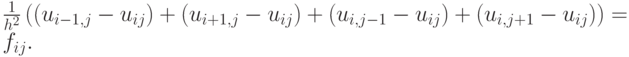
$\frac{1}{{h^2}} \left({(u_{i - 1, j} - u_{ij}) + (u_{i + 1, j} - u_{ij}) + (u_{i, j - 1} - u_{ij}) + (u_{i, j + 1} - u_{ij})}\right) = f_{ij}.$

В силу сделанного предположения, хотя бы одна из скобок в левой части отрицательна, а остальные неположительны. Тогда в левой части стоит отрицательное число, в то время как в правой — положительное (по условиям леммы). Получившееся противоречие возникло из - за предположения о том, что максимальное значение сеточная функция принимает во внутренней точке сеточной области. Лемма доказана.

Лемма 2.Пусть сеточная функция { u_ml } определена на сетке (x_m, y_l) (m, l = 0, ... , M) и во всех внутренних узлах сетки удовлетворяет уравнению

$\frac{{u_{{m} - 1, l} - 2u_{ml} + u_{{m} + 1, l}}}{{{h}^2}} + \frac{{u_{{m}, l - 1} - 2u_{ml} + u_{{m}, l + 1}}}{{{h}^2}} = f_{ml},$

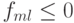причем во всех внутренних узлах сетки правая часть этого уравнения неположительная: ${f_{ml} \le 0}$ . Тогда наименьшее значение сеточная функция u_ml достигает хотя бы в одной точке границы сеточной области.

Доказательство от противного практически повторяет доказательство предыдущей леммы.

Лемма 3 (сеточный принцип максимума). Каждое решение разностного уравнения Лапласа

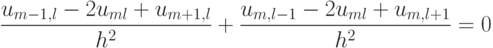
$\frac{{u_{{m} - 1, l} - 2u_{ml} + u_{{m} + 1, l}}}{{{h}^2}} + \frac{{u_{{m}, l - 1} - 2u_{ml} + u_{{m}, l + 1}}}{{{h}^2}} = 0$

достигает своего минимального и максимального значения на границе сеточной области.

Доказательство очевидно — это объединение утверждений леммы 1 и леммы 2.

Введем норму сеточной функции как

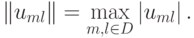
$\left\| {u_{ml}}\right\| = \max\limits_{{m}, l \in D} \left| {u_{ml}}\right|.$

Для доказательства устойчивости теперь надо доказать однозначную разрешимость разностной задачи для уравнения Пуассона с любой правой частью и любыми граничными условиями, получить оценку

$\left\| {u_{ml}}\right\| \le C \left\| f\right\|.$

Здесь в правой части стоит норма правой части задачи, записанной в операторном виде, 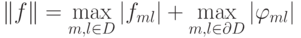$\left\| f\right\| = \max\limits_{{m}, l \in D} \left|{f_{ml}}\right| + \max\limits_{{m}, l \in {\partial}D}\left| {\varphi_{ml}}\right|$ . Первый максимум в этой сумме берется по всем внутренним точкам, второй — по всем точкам сеточной границы.

Докажем однозначную разрешимость разностной задачи. Рассмотрим сеточное уравнение Лапласа с нулевыми граничными условиями. В силу принципа максимума такая задача имеет лишь тривиальное решение. Но сеточная система — это система линейных уравнений. Если система с нулевой правой частью имеет лишь тривиальное решение, то она однозначно разрешима при любой правой части.

Заметим, что в точной арифметике действие разностного оператора, приближающего дифференциальный оператор Лапласа, на произвольный полином второй степени совпадает по результату с действием дифференциального оператора — погрешность аппроксимации, как следует из приведенной выше оценки, будет нулевая. Рассмотрим вспомогательную функцию

$P^{h} = \frac{1}{4} \left[{R^2 - (x^2 + y^2 )}\right] \max\limits_{{m}, l \in D} \left| {f_{ml}}\right| + \max\limits_{{m}, l \in {\partial}D} \left|{\varphi_{ml}}\right|,$

где R — радиус окружности с центром в точке (0, 0) и включающей в себя рассматриваемую область. В данном случае 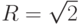$R = \sqrt{2}$ . Эта функция иногда называется мажорантой Гершгорина.

Индекс h означает, что рассматривается сеточная проекция мажоранты. Обратимся к сеточной функции ${w}_{ml} = u_{ml} - P_{ml}^{h}$ и применим к ней разностный оператор Лапласа. Получим ${ \mathbf{\Lambda}}_1 w_{ml} + {\mathbf{\Lambda}}_2 w_{ml} = f_{ml} + \max\limits_{m, l \in D} \left| {f_{ml}}\right|$ во всех внутренних точках области. Отсюда следует, что свое наибольшее значение рассматриваемая сеточная функция достигает на границе сеточной области в соответствии с доказанной леммой 1. Но, как легко убедиться, на границе области сеточная функция ${w}_{ml} = u_{ml} - P_{ml}^{h}$ принимает только отрицательные значения. 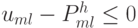Тогда $u_{ml} - P_{ml}^{h} \le 0$ во всех точках сеточной области, включая граничные. Рассмотрим сеточную функцию $v_{ml} = u_{ml} + P_{ml}^{h}$ . 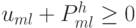Проведя такие же рассуждения, придем к неравенству $u_{ml} + P_{ml}^{h} \ge 0$ во всех точках сеточной области, включая граничные.

Объединяя полученные результаты, находим

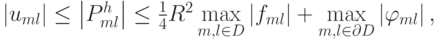
$\left| {u_{ml}}\right| \le \left| {P_{ml}^{h}}\right| \le \frac{1}{4}R^2 \max\limits_{m, l \in D} \left| {f_{ml}}\right| + \max\limits_{m, l \in {\partial}D} \left|{\varphi_{ml}}\right|,$

откуда следует неравенство 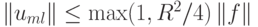$\left\|{u_{ml}}\right\| \le \max (1, {{R^2}/4}) \left\|{f}\right\|$ . Таким образом, устойчивость самой разностной схемы доказана.

Дальше >>

Авторизоваться

Численные методы решения уравнений в частных производных

Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона

Вопросы и ответы