Численные методы решения уравнений в частных производных
[+]
Лекция 6:

Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона
A
|
версия для печати
< Лекция 5 || Лекция 6: 123456789101112 || Лекция 7 >

6.2. Методы решения сеточных уравнений

При решении эллиптических систем существенная часть вычислительной работы — решение возникающих сеточных уравнений. Фактически для нахождения сеточной функции решения надо получить решение системы линейных уравнений большой размерности с разреженной матрицей специального вида. При аппроксимации уравнения Лапласа или Пуассона на регулярных сетках матрица системы самосопряженная. Методы решения таких систем рассмотрим ниже. Перед чтением данного раздела рекомендуется просмотреть лекцию 2 курса "Введение в вычислительную математику".

6.2.1. Метод простых итераций

Наиболее эффективные алгоритмы для численного решения полученной СЛАУ — итерационные. Действительно, прямые методы требуют вычисления обратной матрицы, обратная матрица получается заполненной. Пусть u_{ml}^0 — начальное приближение, выбирать которое желательно как можно ближе к искомому решению, u_{ml}^1, u_{ml}^2 , \ldots — последующие приближения. Верхний индекс в данных обозначениях указывает номер итерации.

Если выполняется условие

\left\| {u_{ml}^{i} - u_{ml}}\right\| \to 0

где uml — проекция точного решения на сетку, то итерационный метод является сходящимся. Оценка сходимости при этом может быть получена в виде

\left\| {u_{ml}^{i + 1} - u_{ml}^{i}}\right\| \le cq^{i},

где C — константа, 0 < q < 1. Итерации продолжаются до тех пор, пока не выполнено условие \left\| {u_{ml}^{i + 1} - u_{ml}^{i}}\right\| \le {\varepsilon}, где \varepsilon — заданная точность. В таком случае можно оценить количество итераций, необходимое для достижения этой точности i \approx \left[{\ln ({\varepsilon}/c)/ \ln q}\right] + 1. Квадратные скобки в этой записи — операция взятия целой части числа.

Метод простых итераций записывается для системы сеточных уравнений в следующем виде: 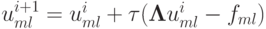u_{ml}^{i + 1} = u_{ml}^{i} +{\tau}({\mathbf{\Lambda}}u_{ml}^{i} - f_{ml}), если точка принадлежит внутренней части сеточной области, и u_{ml}^{i} = \varphi_{ml} если точка с индексами ml принадлежит границе сеточной области. Здесь {\mathbf{\Lambda}} = {\mathbf{\Lambda}}_1 + {\mathbf{\Lambda}}_2 , \tau — итерационный параметр. Количество арифметических операций при реализации метода простых итераций \sim O(N^2).

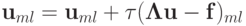Получим формулу для эволюции погрешности. Вычтем из итерационной формулы {\mathbf{u}}_{ml}^{i + 1} = {\mathbf{u}}_{ml}^{i} + \tau ({\mathbf{{\Lambda}u}}^{i} - {\mathbf{f}})_{ml} очевидное тождество {\mathbf{u}}_{ml} = {\mathbf{u}}_{ml} +{\tau}({\mathbf{{\Lambda}u}} - {\mathbf{f}})_{ml} во внутренних точках, а из равенства 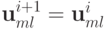{\mathbf{u}}_{ml}^{i + 1} = {\mathbf{u}}_{ml}^{i} вычтем тождество {\mathbf{u}}_{ml} = {\mathbf{u}}_{ml} в граничных узлах. 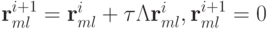Тогда получим \mathbf{r}_{ml}^{i + 1} = \mathbf{r}_{ml}^{i} +{\tau}\Lambda \mathbf{r}_{ml}^{i}, \mathbf{r}_{ml}^{i + 1} = 0, во внутренних и граничных узлах соответственно. Здесь {\mathbf{r}}_{ml}^{i} = {\mathbf{u}}_{ml}^{i} - {\mathbf{u}}_{ml} — невязка на i итерации.

В таком случае для сеточной функции невязки rml, равной нулю на границе, ее эволюция описывается уравнением

r_{ml}^{i + 1} = ({\mathbf{E}} +{\tau}{\mathbf{\Lambda}})r_{ml}^{i}.

Для оценки сходимости итерационного процесса необходимо перейти к неравенству для норм, например евклидовых, и оценить норму оператора перехода

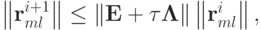
\left\| {{\mathbf{r}}_{ml}^{i + 1}}\right\| \le \left\| {{\mathbf{E}} + \tau {\mathbf{\Lambda}}}\right\| \left\|{{\mathbf{r}}_{ml}^{i}}\right\|,

откуда получим

\left\| {{\mathbf{r}}_{ml}^{i}}\right\| \le \left\| {{\mathbf{E}} + \tau {\mathbf{\Lambda}}}\right\|^{i} \left\|{{\mathbf{r}}_{ml}^0 }\right\|.

Наиболее простым для этих целей является метод Фурье (или спектральный анализ оператора перехода).

Непосредственной проверкой доказываются два следующих утверждения. Семейство функций

$ \varphi_m^{p} = {\sin}\left({\frac{{mp {\pi}}}{M}}\right) $
являются собственными функциями оператора \Lambda _{1} ; им соответствуют собственные значения
$ {\lambda}^{p} = \frac{4}{h^2} {\sin}^2 \left({\frac{p {\pi}}{2M}}\right). $

Здесь p — номер собственного значения (собственной функции), m — номер сеточного узла; p = 1, ... , M - 1.

Для этого необходимо непосредственной подстановкой убедиться в истинности равенства

{\mathbf{\Lambda}}_1 \varphi_m^{p} = - {\lambda}^{p}\varphi_m^{p},

или

$ \frac{1}{{h^2}} \left[{{\sin}\frac{{(m - 1)p {\pi}}}{M}- 2 \sin \frac{{mp {\pi}}}{M} + {\sin}\frac{{(m + 1)p {\pi}}}{M}}\right] = \left({- \frac{4}{{h^2}} {\sin}^2 \frac{{p {\pi}}}{{2M}}}\right) \sin \left({\frac{{mp {\pi}}}{M}}\right). $

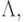Семейство функций {\Psi}_{ml}^{pq} = \varphi_m^{p} \varphi_{l}^{q} является собственными функциями оператора \Lambda, соответствующие собственные значения есть

$ {\lambda}^{pq} = \frac{4}{{h^2}} \left({{\sin}^2 \frac{p \pi}{2M} + {\sin}^2 \frac{q {\pi}}{2M}}\right). $

Равенство \mathbf{\Lambda}{\Psi}_{ml}^{pq} = - \lambda^{pq} {\Psi}_{ml}^{pq} также проверяется непосредственной подстановкой.

В дальнейшем необходимо будет знать границы спектра

$ \lambda_{\min } = {\lambda}^1 = l = \frac{4}{h^2}{\sin}^2 \frac{{\pi}}{2M} \approx {\pi}^2 $
, так как M \gg 1, h = 1/M,

$ \lambda_{\max } = {\lambda}^{(M - 1)} = L = \frac{4}{{h^2}} {\sin}^2 \frac{{(M - 1) {\pi}}}{{2M}} \approx \frac{4}{{h^2}} {\sin}^2 \frac{{\pi}}{2} = \frac{4}{{h^2}} = 4M^2 . $

Для \lambda ^{pq} имеем l \le {\lambda}^{pq} \le L, где l \approx 2 {\pi}^2 , L \approx 8/h^2 = 8M^2. Легко также оценить число обусловленности системы сеточных уравнений.

Дальше >>
< Лекция 5 || Лекция 6: 123456789101112 || Лекция 7 >

Вопросы и ответы

вопросов: 0