НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 6: Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.6. Построение разностных схем для эллиптических уравнений на нерегулярных сетках. Монотонные схемы (подход А.С.Холодова)

В этом разделе будем следовать статье [16.11]. Кроме уравнений Лапласа и Пуассона, в этом разделе будем рассматривать произвольные уравнения эллиптического типа. Рассмотрим задачу

u_xx + e₁₂ u_xy + e₂₂ u_yy + e₁ u_x + e₂ u_y = f(x, y, u)

с условиями на коэффициенты

e_ml(x, y, u) = {e_mlj},  e_m(x, y, u) = {e_mj}, 
m, l = 1, 2,  j = 1, ... , J,  e₂₂ > e₁₂²/4.

Последнее условие обеспечивает эллиптичность задачи. Задача решается в произвольной замкнутой области с несколькими несвязными границами. Предположим сначала, что область не содержит входящих углов (т.е. таких, величина которых больше $\pi$ ). В случае со входящими углами в решении эллиптических задач возникают особенности, во многих случаях необходимо сочетание численных методов и аналитических (асимптотических методов в окрестности входящего угла), подробнее в [16.12]. Индекс j — номер узла сетки; для простоты выкладок узлы сетки нумеруются одним индексом.

Запишем разностную схему для аппроксимации приведенного выше уравнения в каноническом виде

$u_k = \sum\limits_i {\alpha_{{k}{i}} u_i } + f_k , {k} = 1, \ldots , {K}, {i} = {i}_1, \ldots , {i}_i$

- точки, принадлежащие шаблону схемы (см. ниже), $I \ge 5$ , причем неопределенные коэффициенты удовлетворяют условию монотонности ${\alpha}_{ki} \ge 0$ . Здесь K — общее число внутренних сеточных узлов с одноиндексной нумерацией, i₁, ... , i_i — номера расположенных достаточно произвольно в области интегрирования внутренних и граничных сеточных узлов, ${\alpha}_{ki}$ — неопределенные коэффициенты. Часть этих коэффициентов (или все, если I = 5 ) определяются условиями аппроксимации первого порядка или второго порядка на решениях исходного уравнения. Эти условия получаются стандартно — проекция точного решения на нерегулярную сетку раскладывается в ряд Тейлора в окрестности точки u_k. После несложных, но громоздких выкладок получаем, что следующие условия обеспечивают первый порядок аппроксимации:

$\begin{gather*} \sum\limits_i {\alpha_{{k}{i}} = 1}, \\ \sum\limits_i {\alpha_{{k}{i}} X_i (1 - 0.5X_i (e_1 - X_i (e_1^2 + f_u - e_{1x})/3 + Y_i e_{1y})) = 0, } \\ \sum\limits_i {\alpha_{{k}{i}} (Y_i - 0.5X_i^2 (e_2 + X_i (e_2 f_u - e_1 e_2 + e_{2x})/3 - Y_i (f_u - e_{2y}))) = 0, } \\ \sum\limits_i {\alpha_{{k}{i}} X_i (Y_i - 0.5X_i (e_{12} + X_i (e_2 + e_{12x} - 2e_{12} e_1 )/3 + Y_i (e_1 + e_{12y}))) = 0}, \\ \sum\limits_i {\alpha_{{k}{i}} (Y_i^2 - X_i^2 (e_{22} - X_i (e_{12} e_2 + e_{22} e_1 - e_{22x})/3 + Y_i (e_2 + e_{22y}))) = 0, } \\ {\beta}_0 = - \sum\limits_i {\alpha_{{k}{i}} X_i^2(1 - e_1 X_i )/3)/2} = 0. \end{gather*}$

Суммирование ведется по всем точкам, включенным в шаблон. Если к приведенным выше условиям добавить условия

$\begin{gather*} \sum\limits_i {\alpha_{{k}{i}} X_i (3Y_i (Y_i - e_{12} X_i ) - X_i^2 (e_{22} - e_{12}^2 )) = 0}, \\ \sum\limits_i {\alpha_{{k}{i}} (Y_i^3 - e_{22}X_i^2 (3Y_i - e_{12} X_i )) = 0}, \\ {\beta}_1 = - \sum\limits_i {\alpha_{{k}{i}} X_i^3 /6 = 0, }{\beta}_2 = - \sum\limits_i {\alpha_{{k}{i}} X_i^2Y_i /2 = 0}, \end{gather*}$

то схема имеет второй порядок аппроксимации на решениях. Здесь введены обозначения X_i = x_i - x_k, Y_i = y_i - y_k.

В обычных разностных методах шаблон фиксирован (т.е. все внутренние точки сетки имеют одинаковое число соседей). В данном подходе для каждой рассчитываемой точки k = 1, ... , K специальным образом подбираются соседи (сеточный шаблон) так, чтобы выполнялись условия неотрицательности коэффициентов 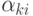${\alpha}_{ki}$ в канонической форме записи разностной схемы. Эти условия обеспечивают неотрицательность разностного оператора ( мажорантность схемы ).

Получающийся в результате решения уравнений для условий аппроксимации первого порядка и неравенств, обеспечивающих монотонность схемы, для каждого k = 1, ... , K набор коэффициентов 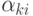${\alpha}_{ki}$ приводит к знакопостоянной линейной (или нелинейной для квазилинейных уравнений) системе уравнений

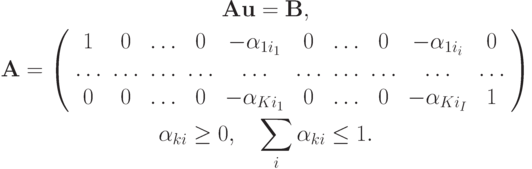
$\begin{gather*} {\mathbf{Au}} = {\mathbf{B}}, \\ {\mathbf{A}} = \left( \begin{array}{cccccccccc} 1 & 0 & \ldots & 0 & {-{\alpha}_{1i_1}} & 0 & \ldots & 0 & {-{\alpha}_{1i_i }} & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & 0 & {-{\alpha}_{Ki_1}} & 0 & \ldots & 0 & {-{\alpha}_{Ki_I }} & 1 \\ \end{array} \right) \\ {\alpha}_{ki} \ge 0, \quad \sum\limits_i {\alpha_{ki} \le 1}. \end{gather*}$

Условия неотрицательности неопределенных коэффициентов обеспечивают выполнение достаточных условий сходимости и принципа максимума, в том числе, при разрывных граничных условиях. Тогда простейший итерационный метод Якоби

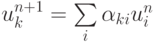
$u_k^{n + 1} = \sum\limits_i {\alpha_{ki} u_i^{n}}$

является сходящимся.

Можно показать, что при весьма слабых ограничениях на расположение сеточных узлов в области интегрирования такие схемы могут быть конструктивно построены. Этот же подход распространен на случай схем со вторым порядком аппроксимации на решениях.

Дальше >>

Авторизоваться

Численные методы решения уравнений в частных производных

Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона

6.6. Построение разностных схем для эллиптических уравнений на нерегулярных сетках. Монотонные схемы (подход А.С.Холодова)

Вопросы и ответы