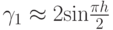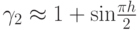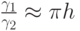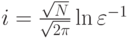НОУ ИНТУИТ | Численные методы решения уравнений в частных производных. Лекция 6: Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1275 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.3. Попеременно - треугольный итерационный метод

При аппроксимации уравнений Пуассона или Лапласа получается система сеточных уравнений

${\mathbf{Au}} = {\mathbf{f}},$

без ограничения общности считаем оператор (матрицу системы) самосопряженным и положительно определенным. Сеточный оператор Лапласа самосопряжен — это легко доказать, но отрицателен. Для того чтобы получить систему уравнений с положительным оператором, достаточно правую и левую части системы умножить на - 1. Здесь $\mathbf{A}$ — квадратная матрица размером N x N.

Зададим матрицу 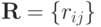${\mathbf{R}} = \{r_{ij} \}$ :

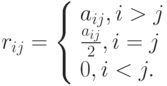
$r_{ij} = \left\{ \begin{array}{l} a_{ij}, i > j \\ \frac{{a_{ij}}}{2}, i = j \\ 0, i < j. \\ \end{array} \right.$

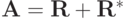В таком случае $\mathbf{A}$ можно представить в виде суммы двух треугольных матриц ${\mathbf{A}} = {\mathbf{R}} + {\mathbf{R}}^*$ .

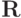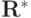$\mathbf{R}$ и $\mathbf{R}^*$ — нижняя и верхняя треугольные матрицы, а их диагональные элементы совпадают. Далее будем рассматривать систему сеточных уравнений как операторное уравнение в конечномерном евклидовом пространстве (унитарном в комплексном случае).

Попеременно - треугольный итерационный метод (ПТИМ) может быть представлен в каноническом виде

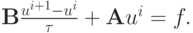
${\mathbf{B}} \frac{{u^{i + 1} - u^{i}}}{\tau} + {\mathbf{A}}u^{i} = f.$

Здесь 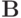$\mathbf{B}$ — самосопряженный положительный оператор. Его часто называют оператором предобуславливания. Для рассматриваемого метода оператор предобуславливания представляется в виде произведения

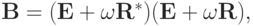
${\mathbf{B}} = ({\mathbf{E}} + \omega {\mathbf{R}}^*)({\mathbf{E}} + \omega {\mathbf{R}}),$

где 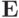$\mathbf{E}$ — единичный оператор, 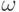$\omega$ — параметр (действительное число).

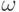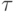При известных $\omega$ и $\tau$ значение u_{k + 1} находится в два этапа. Сначала вычисляется невязка на итерации 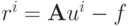$r^{i} = {\mathbf{A}}u^{i} - f$ , а затем решается система матричных уравнений

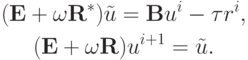
$\begin{gather*} ({\mathbf{E}} + \omega {\mathbf{R}}^*) \tilde{u} = {\mathbf{B}}u^{i} -{\tau}r^{i}, \\ ({\mathbf{E}} + \omega {\mathbf{R}})u^{i + 1} = \tilde{u}. \end{gather*}$

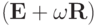Поскольку матрицы $({\mathbf{E}} + \omega {\mathbf{R}}^* )$ и $({\mathbf{E}} + \omega {\mathbf{R}})$ являются треугольными, то эти уравнения решаются значительно проще, чем исходное.

Для формулирования теоремы о ПТИМ введем понятие операторного неравенства: будем полагать, что ${\mathbf{A}} \le {\mathbf{B}}$ , если для любой сеточной функции, не равной нулю тождественно, выполнено неравенство

$(({\mathbf{A}} - {\mathbf{B}}){\mathbf{u}}, {\mathbf{u}}) \ge 0.$

Теорема (без доказательства). Пусть 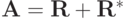${\mathbf{A}} = {\mathbf{R}} + {\mathbf{R}}^*$ и существуют положительные постоянные 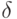$\delta$ и $\Delta,$ при которых выполнены неравенства

${\mathbf{A}} \ge \delta {\mathbf{E}}, 4{\mathbf{R}}^*{\mathbf{R}} \le \Delta {\mathbf{A}}.$

Пусть также

$\omega = \frac{2}{\sqrt{\delta \Delta }},$

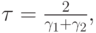
${\tau} = \frac{2}{\gamma_1 + \gamma_2},$

где

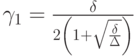
$\gamma_1 = \frac{\delta }{2 \left({1 + \sqrt{\frac{\delta }{\Delta}}}\right)}$

,

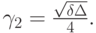
$\gamma_2 = \frac{\sqrt{\delta \Delta }}{4}.$

Тогда двухэтапный итерационный метод

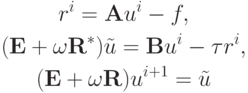
$\begin{gather*} r^{i} = {\mathbf{A}}u^{i} - f, \\ ({\mathbf{E}} + \omega {\mathbf{R}}^*) \tilde{u} = {\mathbf{B}}u^{i} -{\tau}r^{i}, \\ ({\mathbf{E}} + \omega {\mathbf{R}})u^{i + 1} = \tilde{u} \end{gather*}$

сходится, причем для его погрешности справедлива оценка

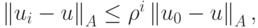
$\left\| {u_i - u}\right\|_{A} \le {\rho}^{i} \left\| {u_0 - u}\right\|_{A},$

где

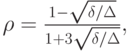
${\rho} = \frac{{1 - \sqrt{\delta / \Delta }}}{{1 + 3 \sqrt{\delta / \Delta }}},$

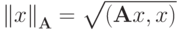$\left\| x\right\|_{\mathbf{A}} = \sqrt{({\mathbf{A}}x, x)}$ .

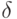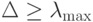В качестве $\delta$ можно взять минимальное собственное значение $\lambda _{min}$ оператора $\mathbf{A}$ , либо любую положительную постоянную ${s} \le \lambda_{\min }$ . Можно показать, что $\Delta \ge \lambda_{\max }$ , $\Delta > \delta$ , где $\lambda _{max}$ — максимальное собственное значение оператора $\mathbf{A}$ .

Рассмотрим применение ПТИМ к численному решению уравнения Пуассона (знак минус ставим для удобства записи):

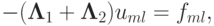
$- ({\mathbf{\Lambda}}_1 + {\mathbf{\Lambda}}_2 )u_{ml} = f_{ml},$

с нулевыми граничными условиями

u_m0 = u_mN = u_0l = u_Nl = 0.

Эта задача может быть представлена как операторное уравнение, где ${\mathbf{A}}u_{ml} = - ({\mathbf{\Lambda}}_1 + {\mathbf{\Lambda}}_2 )u_{ml} m, l = 1, \ldots , N - 1$ . Оператор будет самосопряженным и положительным.

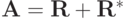Далее необходимо представить матрицу $\mathbf{A}$ в виде ${\mathbf{A}} = {\mathbf{R}} + {\mathbf{R}}^*$ и определить константы 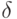$\delta$ и $\Delta.$

Рассмотрим разностную аппроксимацию уравнения Пуассона по схеме "крест", переписав схему в эквивалентном виде:

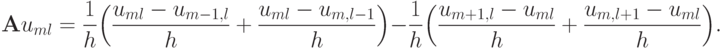
${\mathbf{A}}u_{ml} = \frac{1}{h} \Bigl({\frac{{u_{ml} - u_{m - 1, l}}}{h} + \frac{{u_{ml} - u_{m, l - 1}}}{h}} \Bigr) - \frac{1}{h} \Bigl({\frac{{u_{m + 1, l} - u_{ml}}}{h} + \frac{{u_{m, l + 1} - u_{ml}}}{h}} \Bigr).$

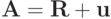Тем самым представили оператор $\mathbf{A}$ как сумму двух операторов $\mathbf{A} = \mathbf{R} + \mathbf{u}$ , где

$\begin{gather*} {\mathbf{R}}u_{ml} = \frac{1}{h} \left({\frac{{u_{ml} - u_{m - 1, l}}}{h} + \frac{{u_{ml} - u_{m, l - 1}}}{h}}\right), \\ {\mathbf{R}}^*u_{ml} = - \frac{1}{h} \left({\frac{{u_{m + 1, l} - u_{ml}}}{h} + \frac{{u_{m, l + 1} - u_{ml}}}{h}}\right). \end{gather*}$

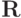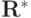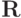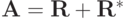При этом матрица оператора $\mathbf{R}$ является нижней треугольной, а матрица $\mathbf{R}^*$ — верхней треугольной (в этом легко убедиться, записав рассматриваемую систему в виде СЛАУ). Можно также показать, что оператор $\mathbf{u}$ является сопряженным оператором к $\mathbf{R}$ , т.е. $\mathbf{A} = \mathbf{R} + \mathbf{R}^*$ .

Также показывается, что

$\delta = \frac{8}{{h^2}} {\sin}^2 \frac{{{\pi}h}}{2} = \lambda_{\min } ({\mathbf{A}}), \Delta = \frac{8}{{h^2}} \ge \frac{8}{{h^2}} {\cos}^2 \frac{{{\pi}h}}{2} = \lambda_{\max } ({\mathbf{A}}).$

Воспользовавшись формулами для 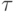$\tau$ и $\omega,$ получим

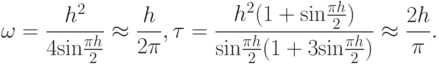
$\omega = \frac{{h^2}}{{4 {\sin}\frac{{{\pi}h}}{2}}} \approx \frac{h}{{2 {\pi}}},{\tau} = \frac{{h^2 (1 + {\sin}\frac{{{\pi}h}}{2})}}{{{\sin}\frac{{{\pi}h}}{2} (1 + 3 {\sin}\frac{{{\pi}h}}{2})}} \approx \frac{{2h}}{{\pi}}.$

Оценка количества итераций для этого метода дает

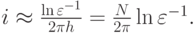
$i \approx \frac{{\ln {\varepsilon}^{- 1}}}{{2 {\pi}h}} = \frac{N}{{2 {\pi}}} \ln {\varepsilon}^{- 1} .$

Напомним, что границы спектра для рассматриваемого оператора 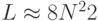$L \approx 8N^{2}2$ ,

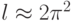
$$ l \approx 2 {\pi}^2$

и $N \approx \frac{{\pi}}{2} \sqrt{L/l} $$ .

Алгоритм вычисления 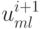$u_{ml}^{i + 1}$ , в соответствии с ранее приведенными формулами двух этапов ПТИМ будет таков.

Первый этап:

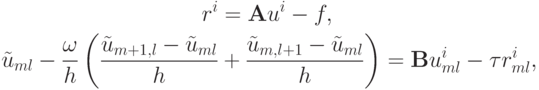
$\begin{gather*} r^{i} = {\mathbf{A}}u^{i} - f, \\ \tilde{u}_{ml} - \frac{\omega}{h} \left(\frac{\tilde{u}_{m + 1, l} - \tilde{u}_{ml}}{h} + \frac{\tilde{u}_{m, l + 1} - \tilde{u}_{ml}}{h}\right) = \mathbf{B}u^{i}_{ml} - {\tau}r^{i}_{ml}, \end{gather*}$

второй этап:

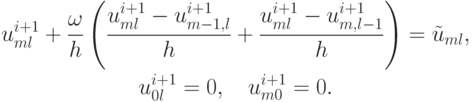
$\begin{gather*} u^{i + 1}_{ml} + \frac{\omega}{h} \left( \frac{u^{i + 1}_{ml} - u^{i + 1}_{m - 1, l}}{h} + \frac{u^{i + 1}_{ml} - u^{i + 1}_{m, l - 1}} {h}\right) = \tilde{u}_{ml}, \\ u_{0l}^{i + 1} = 0, \quad u_{m0}^{i + 1} = 0. \end{gather*}$

Уравнение для $\tilde{u}_{ml}$ нужно начинать решать от точки m = N - 1, l = N - 1, учитывая, что на границе сеточной области сеточная функция равна нулю. Таким образом, вычисления ведутся рекуррентно. Система решается, начиная с правого верхнего угла области до левого нижнего угла. Система линейных уравнений, соответствующая второму этапу, решается аналогично, но вычисления здесь начинаются в точке m = 1, l = 1 и заканчивается в точке m = N - 1, l = N - 1.

Метод по своим идеям напоминает схему Саульева, рассмотренную ранее в одномерном варианте при решении уравнений параболического типа.

Использование в ПТИМ набора чебышевских итерационных параметров приводит к следующему результату. Расчетные формулы для метода таковы:

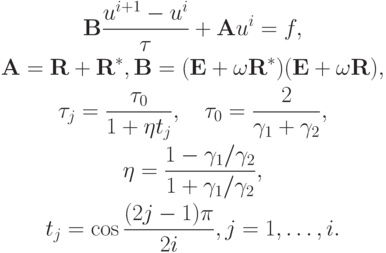
$\begin{gather*} {\mathbf{B}} \frac{{u^{i + 1} - u^{i}}}{\tau} + {\mathbf{A}}u^{i} = f, \\ {\mathbf{A}} = {\mathbf{R}} + {\mathbf{R}}^*, {\mathbf{B}} = ({\mathbf{E}} + \omega { \mathbf{R}}^*)({\mathbf{E}} + \omega {\mathbf{R}}), \\ \tau_j = \frac{{\tau_0 }}{{1 + \eta t_j}}, \quad \tau_0 = \frac{2}{{\gamma_1 + \gamma_2}}, \\ \eta = \frac{1 - {\gamma_1}/{\gamma_2}}{1 + {\gamma_1}/{\gamma_2}}, \\ t_j = \cos \frac{{(2j - 1) {\pi}}}{{2i}}, j = 1, \ldots , i. \end{gather*}$