Диагностическая задача в интервальной постановке
Пусть 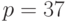 и необходимо найти все решения системы
и необходимо найти все решения системы
![\begin {cases}
3x_1+5x_2=[30,36],\\
5x_1+2x_2=[20,30]
\end {cases}](/sites/default/files/tex_cache/0fac30ec8c9776cf6abece5392c71a4a.png)
Вначале рассмотрим систему вида (20.4):
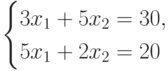
Решение этой системы есть пара  .
.
Теперь рассмотрим две системы вида (20.5):

Их решениями являются 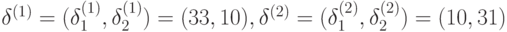 .
.
Тогда все множество решений системы таково:

где
Таким образом, получаем:

Все эти решения представлены в следующей таблице:
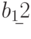 |
20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | (6, 32 | (16, 26) | (26, 20) | (36, 14) | (9, 8) | (19, 2) | (29, 33) | (2, 27) | (12, 21) | (22, 15) | (32, 9) | |
| 31 | (2, 5) | (12, 36) | (22, 30) | (32, 24) | (5, 18) | (15, 12) | (25, 6) | (35, 0) | (8, 31) | (18, 25) | (28, 19) | |
| 32 | (35, 15) | (8, 9) | (18, 3) | (28, 34) | (1, 28) | (11, 22) | (21, 16) | (31, 10) | (4, 4) | (14, 35) | (24, 29) | |
| 33 | (31, 25) | (4, 19) | (14, 13) | (24, 7) | (34, 1) | (7, 32) | (17, 26) | (27, 20) | (0, 14) | (10, 8) | (20, 2) | |
| 34 | (27, 35) | (0, 29) | (10, 23) | (20, 17) | (30, 11) | (3, 5) | (13, 36) | (23, 30) | (33, 24) | (6, 18) | (16, 12) | |
| 35 | (23, 8) | (33, 2) | (6, 33) | (16, 27) | (26, 21) | (36, 15) | (9, 9) | (19, 3) | (29, 34) | (2, 28) | (12, 22) | |
| 36 | (19, 18) | (29, 12) | (2, 6) | (12, 0) | (22, 31) | (32, 25) | (5, 19) | (15, 13) | (25, 7) | (35, 1) | (8, 32) |
Таким образом, в рассмотренном примере предлагаемый метод отыскания всех решений СЛАУ потребовал решения 3 систем линейных уравнений вместо 77 при использовании тривиального метода.
Теперь проиллюстрируем применение метода решения СЛАУ на конкретной диагностической задаче.
Рассмотрим ЛА над полем 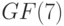 , заданный с помощью характеристических матриц, которые приведены выше в этом разделе. Пусть множество допустимых начальных состояний содержит 4 состояния:
, заданный с помощью характеристических матриц, которые приведены выше в этом разделе. Пусть множество допустимых начальных состояний содержит 4 состояния:
![\{[203]', [001]', [456]', [105]'\}](/sites/default/files/tex_cache/79e344fa2ab23b430f5f5942505891ad.png)
Диагностическая последовательность для заданного множества допустимых начальных состояний, построенная с использованием описанного выше диагностического дерева, такова: ![u(0)=[0], u(1)=[0], u(2)=[0]](/sites/default/files/tex_cache/5ba67181826c935f995d29e78d1ce63f.png) . Предположим, что измерения выходной реакции ЛА на эту диагностическую последовательность дали следующие результаты:
. Предположим, что измерения выходной реакции ЛА на эту диагностическую последовательность дали следующие результаты:
![y(0)=
\left [
\begin {matrix}
[5,6]\\
[2,4]
\end {matrix}
\right ],
y(1)=
\left [
\begin {matrix}
[0,2]\\
[0,1]
\end {matrix}
\right ],
y(2)=
\left [
\begin {matrix}
[0,1]\\
[3,5]
\end {matrix}
\right ]](/sites/default/files/tex_cache/67eb9fa4f4c809b617987b08c79260b7.png)
Заметим, что эти результаты получены в несколько иных предположениях об искажениях при измерении, чем были сделаны при построении фрагмента интервального диагностического дерева на рис.20.2.
Для решения интервальной диагностической задачи необходимо найти все решения системы уравнений вида (20.2).
![\left [
\begin {matrix}
5&0&3\\
1&4&6\\
5&5&2\\
5&2&6\\
6&1&3\\
3&2&3
\end {matrix}
\right ]
\left [
\begin {matrix}
s_1(0)\\
s_2(0)\\
s_3(0)
\end {matrix}
\right ]=
\left [
\begin {matrix}
[5,6]\\
[2,4]\\
[0,2]\\
[0,1]\\
[0,1]\\
[3,5]
\end {matrix}
\right ]](/sites/default/files/tex_cache/0c41efbdacca82d567f9be3f65d11860.png) |
( 20.7) |
Заметим, что для нахождения решения этой интервальной системы уравнений тривиальным способом необходимо решить 216 систем.
Для приведенной системы количество неизвестных равно 3, а число уравнений равно 6. Приводя матрицу к квадратной, получаем следующую систему:
![\left [
\begin {matrix}
5&0&3\\
1&4&6\\
5&5&2
\end {matrix}
\right ]
\left [
\begin {matrix}
s_1(0)\\
s_2(0)\\
s_3(0)
\end {matrix}
\right ]=
\left [
\begin {matrix}
[5,6]\\
[2,4]\\
[0,2]
\end {matrix}
\right ]](/sites/default/files/tex_cache/4e1e7b20529d7342d1a65b2c80441766.png) |
( 20.8) |
Обозначим матрицу полученной системы (20.8) через  . В соответствии с описанным выше методом необходимо решить следующие 4 системы линейных уравнений:
. В соответствии с описанным выше методом необходимо решить следующие 4 системы линейных уравнений:
![F[\xi_1 \xi_2 \xi_3]'=[0 0 0]',\\
f[\delta_1^{(1)} \delta_2^{(1)} \delta_3^{(1)}]'=[100]',\\
F[\delta_1^{(2)} \delta_2^{(2)} \delta_3^{(2)}]'=[010]',\\
F[\delta_1^{(3)} \delta_2^{(3)} \delta_3^{(3)}]'=[001]'](/sites/default/files/tex_cache/acf9e43174909372b610847420e26931.png)
Решая их, получаем следующие результаты:
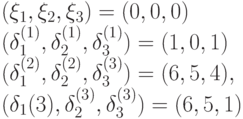
Теперь в соответствии с формулой (20.6) выпишем решение системы (20.7) в параметрическом виде:
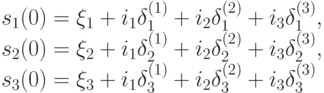
где 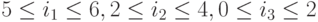
Таким образом, получаем 18 решений системы уравнений (20.8), представленных в формате ![s(0)=[s_1(0), s_2(0), s_3(0)]'](/sites/default/files/tex_cache/e9b622c0870d67d56e43fb2e460ba21e.png) :
:
![[336]', [120]', [611]', [213]', [004]', [565]', [160]', [651]', [442]',](/sites/default/files/tex_cache/c550e3d012042c2459a18f4a42f21d33.png)
![[430]', [221]', [012]', [314]', [105]', [666]', [261]', [052]', [543].](/sites/default/files/tex_cache/519ee576428ca6ab468a5db9b7890883.png)
Полученные решения интервальной системы уравнений (20.8) являются "кандидатами" в решение интервальной системы уравнений (20.7). Подставляя их в систему (20.7), можно убедиться, что только одно из этих 18 решений, ![s(0)=[105]'](/sites/default/files/tex_cache/9a5724a3428403c23de145b7aabb12d2.png) , удовлетворяет всем уравнениям (20.7). Поскольку это решение принадлежит множеству допустимых начальных состояний рассматриваемого ЛА, то оно и есть искомое решение интервальной диагностической задачи.
, удовлетворяет всем уравнениям (20.7). Поскольку это решение принадлежит множеству допустимых начальных состояний рассматриваемого ЛА, то оно и есть искомое решение интервальной диагностической задачи.
Генетический алгоритм для решения интервальной диагностической задачи
В предыдущем разделе было указано, что мощность множества всех решений интервальной системы уравнений с квадратной матрицей равна величине 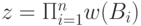 . Из формулы видно, что эта мощность быстро растет с ростом ширины интервалов в правой части системы (20.3). Даже при сравнительно небольших значениях упомянутых параметров величина
. Из формулы видно, что эта мощность быстро растет с ростом ширины интервалов в правой части системы (20.3). Даже при сравнительно небольших значениях упомянутых параметров величина  может быть столь велика, что множество всех решений системы становится практически необозримым. В [24] отмечается, что это свойство является атрибутом труднорешаемой задачи, причем не менее важным, чем экспоненциальное время ее решения. По этой причине, если мощность множества всех "кандидатов" в решение системы очень велика, возникает проблема нахождения среди них единственного решения интервальной диагностической задачи. В данном разделе рассматривается еще один подход к решению поставленной интервальной диагностической задачи, который можно рассматривать как "быстрый" метод ее решения.
может быть столь велика, что множество всех решений системы становится практически необозримым. В [24] отмечается, что это свойство является атрибутом труднорешаемой задачи, причем не менее важным, чем экспоненциальное время ее решения. По этой причине, если мощность множества всех "кандидатов" в решение системы очень велика, возникает проблема нахождения среди них единственного решения интервальной диагностической задачи. В данном разделе рассматривается еще один подход к решению поставленной интервальной диагностической задачи, который можно рассматривать как "быстрый" метод ее решения.
Простейшим способом поиска какого-либо решения рассматриваемой задачи является перебор всех возможных допустимых начальных состояний ЛА и проверка того, удовлетворяют ли эти состояния системе линейных уравнений (20.3). Поскольку для ЛА, заданного над полем  , число таких всевозможных начальных состояний
, число таких всевозможных начальных состояний  , где
, где  - размерность ЛА, то уже при
- размерность ЛА, то уже при 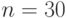 и
и  число состояний, подлежащих проверке, превышает
число состояний, подлежащих проверке, превышает  . Учитывая, что проверка допустимости состояния ЛА является нетривиальной (вычисление матричных произведений), можно констатировать, что проверка всех возможных состояний неосуществима за приемлемое время.
. Учитывая, что проверка допустимости состояния ЛА является нетривиальной (вычисление матричных произведений), можно констатировать, что проверка всех возможных состояний неосуществима за приемлемое время.
Накопленный опыт практического решения задач переборного типа показал достаточно высокую эффективность применения генетических алгоритмов (ГА). Ниже будет показано, каким образом можно построить генетический алгоритм для рассматриваемой в этом разделе задачи, и оценена его эффективность.
Заметим, что используемые далее, но не определенные здесь понятия, связанные с генетическими алгоритмами, заимствованы из [5], [32].
Принцип работы генетических алгоритмов основан на моделировании некоторых механизмов популяционной генетики: манипулировании хромосомным набором при формировании генотипа новой биологической особи путем наследования участков хромосомных наборов родителей (кроссинговер), случайном изменении генотипа (мутация). Другим важным механизмом, заимствованным у природы, является процедура естественного отбора, направленная на улучшение от поколения к поколению приспособленности членов популяции к "выживанию" особей, обладающих определенными признаками.
Применение генетических алгоритмов требует подходящего выбора способа кодирования решения, представленного в виде хромосомы, поскольку их эффективность во многом зависит от этого. Кроме того, целевая функция, применяемая для оценки приспособленности хромосомы, должна быть выбрана соответствующим образом, чтобы адекватно отразить конечную цель поиска. Важными моментами при использовании генетических алгоритмов являются также реализация операторов отбора, скрещивания и мутации и выбор вероятности их применения.
В данной работе используется простой генетический алгоритм (ПГА), который был впервые описан Гольдбергом на основе работ Холланда. Изложение сути этого алгоритма приведено в [32]. ПГА использует операторы отбора (селекции), скрещивания (кроссинговера) и мутации. Механизм ПГА несложен, и ниже кратко описаны его этапы.
- Генерация случайной популяции, состоящей из
 хромосом, длина каждой из которых равна
хромосом, длина каждой из которых равна  (каждая хромосома - кандидат на роль решения задачи). Эта начальная популяция образует поколение с номером 0.
(каждая хромосома - кандидат на роль решения задачи). Эта начальная популяция образует поколение с номером 0. - Вычисление функции приспособленности для каждой хромосомы в популяции.
- Выполнение следующих шагов, пока не будет получено
 потомков:
потомков:- Выбор пары родительских хромосом из текущей популяции, при этом вероятность выбора больше у тех хромосом, чья приспособленность выше. Выбор делается с возвращением, т. е. одна и та же хромосома может быть выбрана в качестве родителя более одного раза.
- С вероятностью
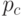 (вероятность кроссинговера) производится кроссинговер пары в произвольно выбранной точке (одноточечный кроссинговер), которая выбирается с равномерно распределенной вероятностью, и формируются два потомка. Если кроссинговер не производится, то формируются два потомка, которые являются точными копиями родителей.
(вероятность кроссинговера) производится кроссинговер пары в произвольно выбранной точке (одноточечный кроссинговер), которая выбирается с равномерно распределенной вероятностью, и формируются два потомка. Если кроссинговер не производится, то формируются два потомка, которые являются точными копиями родителей. - Производится мутация двух потомков в каждом гене с вероятностью
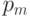 (вероятность мутации), и получившиеся хромосомы помещаются в новую популяцию.
(вероятность мутации), и получившиеся хромосомы помещаются в новую популяцию. - Если
 нечетное и количество потомков равно
нечетное и количество потомков равно 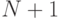 , то один произвольно выбранный потомок удаляется из новой популяции.
, то один произвольно выбранный потомок удаляется из новой популяции.
- Текущая популяция замещается новой популяцией с увеличением номера поколения.
- Если номер текущего поколения меньше заданного максимального числа поколений, то переход к шагу 2, иначе окончание алгоритма.
Остановимся подробнее на отмеченных нами узловых точках построения генетического алгоритма. Обратимся вначале к способу кодирования решения в рассматриваемой интервальной диагностической задаче.
Большая часть существующей теории генетических алгоритмов (включая ранние работы Холланда) базируется на предположении, что хромосомы являются битовыми строками. Таким образом, двоичное кодирование решения является основным способом кодирования решений при использовании генетических алгоритмов.
Каждому допустимому решению  сопоставим битовую строку, представляющую собой хромосому. Сопоставление осуществим следующим образом: вектору
сопоставим битовую строку, представляющую собой хромосому. Сопоставление осуществим следующим образом: вектору ![s=[s_1, s_2, \dots, s_n]'](/sites/default/files/tex_cache/23ade50e3cbdd30f3ab7224967c56e38.png) ' поставим в соответствие число в двоичной системе, которое равно числу
' поставим в соответствие число в двоичной системе, которое равно числу 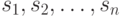 в системе счисления с основанием
в системе счисления с основанием  . Такая схема сопоставления является взаимно-однозначной, что позволяет проводить как кодирование, так и декодирование хромосомы.
. Такая схема сопоставления является взаимно-однозначной, что позволяет проводить как кодирование, так и декодирование хромосомы.
Заметим, что при  используются системы счисления по основанию 2 и перевод производить не требуется. Если
используются системы счисления по основанию 2 и перевод производить не требуется. Если 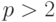 , то число бит, необходимых для представления решения, отличается от
, то число бит, необходимых для представления решения, отличается от  в сторону увеличения.
в сторону увеличения.
При таком способе кодирования длина хромосомы  определяется следующим образом:
определяется следующим образом:
![l=
\begin {cases}
n*k, если\ p=2^k,\\
[\log_2 p^n}+1], если\ p \ne 2^k
\end {cases}](/sites/default/files/tex_cache/984437941b3aeba2e5fd425e17f32399.png)
Пример 1.
Пусть 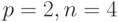 , тогда
, тогда 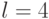 . Решению
. Решению ![s=[1, 0, 1, 1]'](/sites/default/files/tex_cache/e550a8dd7cff2b91be28c58990121c8b.png) соответствует хромосома 1011.
соответствует хромосома 1011.
Пусть  , тогда
, тогда 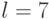 . Решению
. Решению ![s=[1, 0, 2, 1]'](/sites/default/files/tex_cache/881b2c2efd7ce5f1c45cb1c1de029d3b.png) соответствует хромосома 0100010.
соответствует хромосома 0100010.
Следующим важным моментом при реализации генетического алгоритма является определение целевой функции, которая "направляет" поиск решения.
Целевая функция используется для оценивания приспособленности хромосомы. Заметим, что для вычисления значения целевой функции необходимо произвести декодирование хромосомы в соответствующее ей решение.
Пусть ![s=[s_1, s_2, \dots, s_N]'](/sites/default/files/tex_cache/e63d0dba708da697ddd7e12e0801f7d5.png) - решение, которое необходимо оценить. Так как это решение представляет собой предполагаемое начальное состояние, то получаем
- решение, которое необходимо оценить. Так как это решение представляет собой предполагаемое начальное состояние, то получаем 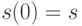 . Осуществляя подстановку
. Осуществляя подстановку 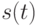 в систему уравнений (1.1)-(1.2) при
в систему уравнений (1.1)-(1.2) при  где
где 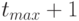 равно длине диагностической последовательности, получим набор из
равно длине диагностической последовательности, получим набор из 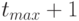 выходных векторов размерности
выходных векторов размерности 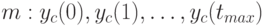 .
.
Целевую функцию определим следующим образом:
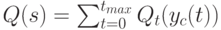 |
( 20.9) |
где
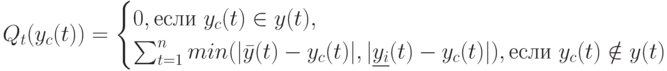 |
( 20.10) |
