Разновидности экспериментов с билинейными автоматами
Эксперименты по распознаванию неизвестного входного слова
БА  назовем БА без потери информации из состояния
назовем БА без потери информации из состояния  (БПИ-
(БПИ-  ), если, зная это состояние и наблюдая выходную последовательность на любую неизвестную входную последовательность, последнюю можно определить однозначно.
), если, зная это состояние и наблюдая выходную последовательность на любую неизвестную входную последовательность, последнюю можно определить однозначно.
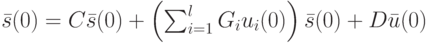
Преобразуем это равенство следующим образом:
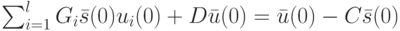 |
( 22.1) |
Будем интерпретировать (22.1) как систему линейных уравнений относительно неизвестных 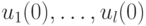 , являющихся координатами вектора
, являющихся координатами вектора  . Условимся матрицу этой системы обозначать через
. Условимся матрицу этой системы обозначать через  и называть матрицей распознавания для состояния
и называть матрицей распознавания для состояния 
Будем говорить, что состояние 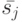 БА
БА  достижимо из состояния
достижимо из состояния 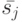 , если существует такая входная последовательность, которая переводит БА из состояния
, если существует такая входная последовательность, которая переводит БА из состояния 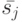 в
в 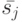 . Обозначим через
. Обозначим через 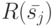 множество тех состояний БА, которые достижимы из состояния
множество тех состояний БА, которые достижимы из состояния 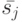 .
.
Теорема 22.1. Для того чтобы БА  был БА БПИ-
был БА БПИ-  , необходимо и достаточно, чтобы для любого состояния
, необходимо и достаточно, чтобы для любого состояния  ) выполнялось условие
) выполнялось условие 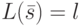 .
.
Доказательство. Очевидно, что неизвестный входной вектор  БА
БА  , стартующего в начальном состоянии
, стартующего в начальном состоянии  , может быть распознан тогда и только тогда, когда система (22.1) имеет единственное решение. Из [33] известно, что необходимым и достаточным условием для этого является равенство ранга этой системы числу
, может быть распознан тогда и только тогда, когда система (22.1) имеет единственное решение. Из [33] известно, что необходимым и достаточным условием для этого является равенство ранга этой системы числу  . Если входной вектор
. Если входной вектор  найден, то по формуле (21.1) легко вычислить следующее состояние
найден, то по формуле (21.1) легко вычислить следующее состояние 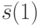 этого БА. Зная его и выходной вектор
этого БА. Зная его и выходной вектор 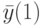 , можно найти вектор
, можно найти вектор 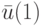 из системы
из системы 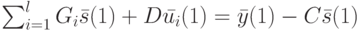 поскольку
поскольку 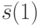 достижимо из
достижимо из  и по условию теоремы ранг матрицы последней системы равен
и по условию теоремы ранг матрицы последней системы равен  . Доказательство леммы получается отсюда по индукции.
. Доказательство леммы получается отсюда по индукции.
Следуя [18], БА  назовем БА БПИ, если для него возможно однозначно определить неизвестную входную последовательность по известному начальному состоянию и наблюдаемой реакции независимо от начального состояния и подаваемой входной последовательности.
назовем БА БПИ, если для него возможно однозначно определить неизвестную входную последовательность по известному начальному состоянию и наблюдаемой реакции независимо от начального состояния и подаваемой входной последовательности.
Теорема 22.2. Для того чтобы БА  был БА БПИ, необходимо и достаточно, чтобы для любого состояния
был БА БПИ, необходимо и достаточно, чтобы для любого состояния  ) был равен l.
) был равен l.
Доказательство теоремы очевидно.
Отметим, что каждый БА БПИ является БА БПИ-  для любого
для любого  , однако, если БА не является сильно связным, то, вообще говоря, не каждый БА БПИ-
, однако, если БА не является сильно связным, то, вообще говоря, не каждый БА БПИ-  будет одновременно и БА БПИ.
будет одновременно и БА БПИ.
Приведем одно достаточное условие принадлежности БА классу БА БПИ.
Теорема 22.3. БА  является БА БПИ, если
является БА БПИ, если ![\sum_{i=1}^lG_i=[0]](/sites/default/files/tex_cache/aa6ad0b2e6c12e1ce9f1c2ca228a8c66.png) и
и 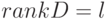 .
.
В этом случае система (22.1) вырождается в систему

откуда и следует справедливость теоремы.
Опишем теперь процедуру нахождения множества  всех состояний БА
всех состояний БА  , достижимых из состояния
, достижимых из состояния  . На первом шаге, полагая в формуле (21.1)
. На первом шаге, полагая в формуле (21.1) 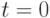 и подставляя в (21.1) все возможные входные векторы
и подставляя в (21.1) все возможные входные векторы  , общее число которых равно
, общее число которых равно 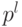 , получим множество всех состояний БА, достижимых из
, получим множество всех состояний БА, достижимых из  входными последовательностями длины 1, которое обозначим через
входными последовательностями длины 1, которое обозначим через  . Построим множество
. Построим множество  . На втором шаге положим в (21.1)
. На втором шаге положим в (21.1) 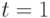 и для каждого
и для каждого 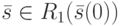 и всех возможных входных векторов
и всех возможных входных векторов 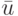 построим множество
построим множество 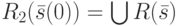 . Положим теперь множество
. Положим теперь множество  . Если мощность только что построенного множества
. Если мощность только что построенного множества  равна мощности множества
равна мощности множества  , полученного на предыдущем шаге, то процедура заканчивается - искомое множество найдено. В противном случае выполнение процедуры продолжается далее аналогичным образом до
, полученного на предыдущем шаге, то процедура заканчивается - искомое множество найдено. В противном случае выполнение процедуры продолжается далее аналогичным образом до 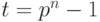 , поскольку любое состояние, достижимое из
, поскольку любое состояние, достижимое из  , может быть достигнуто входной последовательностью, длина которой не превышает числа состояний БА.
, может быть достигнуто входной последовательностью, длина которой не превышает числа состояний БА.
Введем еще одну разновидность автоматов БПИ. БА  назовем БА существенно без потери информации (СБПИ), если, зная только входную последовательность, можно всегда однозначно определить неизвестную входную последовательность, породившую наблюдаемую реакцию.
назовем БА существенно без потери информации (СБПИ), если, зная только входную последовательность, можно всегда однозначно определить неизвестную входную последовательность, породившую наблюдаемую реакцию.
Сформулируем одно достаточное условие принадлежности БА классу БА СБПИ.
Теорема 22.4. БА  является БА СБПИ, если
является БА СБПИ, если ![\sum_{i=1}^lG_i=[0]](/sites/default/files/tex_cache/aa6ad0b2e6c12e1ce9f1c2ca228a8c66.png) ,
, ![C=[0]](/sites/default/files/tex_cache/70a7f5d740509ccc7a96035ee7fff0c0.png) и
и 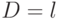 .
.
При выполнении условий теоремы система (22.1) вырождается в систему 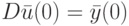 , которая не зависит от начального состояния
, которая не зависит от начального состояния  БА. Отсюда и следует справедливость утверждения.
БА. Отсюда и следует справедливость утверждения.
Эксперименты с билинейными автоматами с запаздыванием
По аналогии с [17] приведем классификацию билинейных автоматов с запаздыванием.
Начнем с общих билинейных систем с распределенным запаздыванием.
Запаздывание по состоянию
Уравнение состояния имеет вид
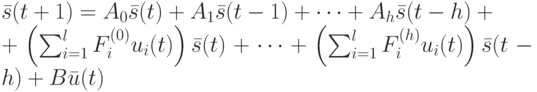 |
( 22.2) |
Уравнение выхода имеет вид
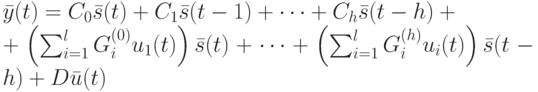 |
( 22.3) |
где 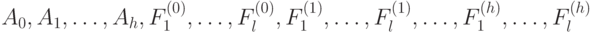 - матрицы размерности
- матрицы размерности  ;
;
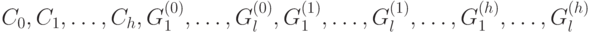 - матрицы размерности
- матрицы размерности  ;
;
 - натуральное число (запаздывание).
- натуральное число (запаздывание).
Все элементы матриц и векторов берутся из основного поля 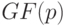 .
.
Запаздывание по управлению
Уравнение состояния имеет вид
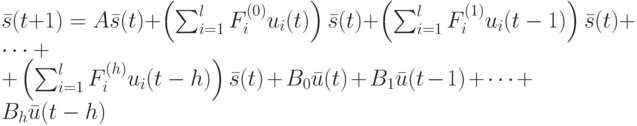 |
( 22.4) |
Уравнение выхода имеет вид
 |
( 13,5) |
Приведем теперь классификацию билинейных автоматов с запаздыванием.
БА с запаздыванием по состоянию
Уравнение состояния имеет вид

Уравнение выхода имеет вид
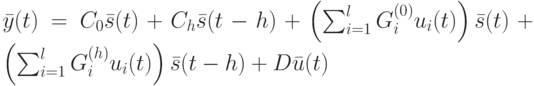
БА с запаздыванием по управлению
Уравнение состояния имеет вид
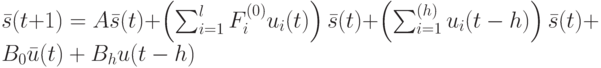
Уравнение выхода имеет вид
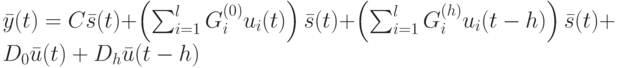
Очевидно, что билинейные автоматы с запаздыванием являются частным случаем общих билинейных систем с распределенным запаздыванием, где соответствующие матрицы (запаздывание на 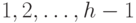 такт) являются нулевыми. Таким образом, все результаты, полученные для билинейных автоматов с распределенным запаздыванием, легко распространить на билинейные автоматы с запаздыванием . Поэтому далее рассматриваются только билинейные автоматы с распределенным запаздыванием.
такт) являются нулевыми. Таким образом, все результаты, полученные для билинейных автоматов с распределенным запаздыванием, легко распространить на билинейные автоматы с запаздыванием . Поэтому далее рассматриваются только билинейные автоматы с распределенным запаздыванием.
Для однозначности определения состояний для 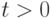 необходимо задать начальные данные: для билинейных автоматов с распределенным запаздыванием по состоянию необходимо задать состояния в моменты времени
необходимо задать начальные данные: для билинейных автоматов с распределенным запаздыванием по состоянию необходимо задать состояния в моменты времени 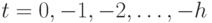 ; для билинейных автоматов с распределенным запаздыванием по управлению необходимо задать начальное состояние в момент времени t = 0, а также входные символы в моменты времени
; для билинейных автоматов с распределенным запаздыванием по управлению необходимо задать начальное состояние в момент времени t = 0, а также входные символы в моменты времени 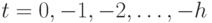 .
.
Для изучения свойств билинейных автоматов с распределенным запаздыванием применим метод, использованный в [71] и уже примененный нами в лекции 3 (часть II) для линейных автоматов с запаздыванием. Он состоит в том, что более сложная система с запаздыванием сводится к эквивалентной ей системе, но уже без запаздывания, однако с большим числом состояний. Так, для билинейного автомата с распределенным запаздыванием необходимо найти эквивалентный ему билинейный автомат. Далее, учитывая специфику характеристических матриц билинейных автоматов, можно получить необходимые и достаточные условия существования синхронизирующих, установочных и диагностических последовательностей для исходного билинейного автомата с распределенным запаздыванием.
Рассмотрим билинейный автомат с распределенным запаздыванием по состоянию. Его состояние в произвольный момент времени  определим как вектор
определим как вектор ![\bar z(t)=[\bar s(t) \bar s(t-1) \dots \bar s(t-h)]^T](/sites/default/files/tex_cache/b5b8d9ffe8c70f7ddd34b0e538cf9c6d.png) . Тогда следующее состояние после подачи очередного входа
. Тогда следующее состояние после подачи очередного входа  будет
будет
![\bar z(t+1)=[\bar s(t+1) \bar s(t) \dots \bar s(t-h+1)]^T](/sites/default/files/tex_cache/575e08765c95bfb30c9e86be274540bc.png)
Начальное состояние ![\bar z(0)=[\bar s(0) \bar s(-1) \dots \bar s(-h)]^T](/sites/default/files/tex_cache/d7341f441e9ab2325150263e73a13152.png) .
.
Тогда билинейный автомат с распределенным запаздыванием по состоянию можно описать следующим образом:
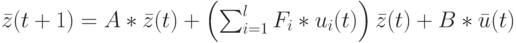 |
( 22.6) |
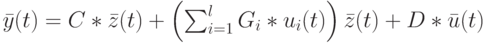 |
( 22.7) |

 -
-  ;
; -
-  ;
;