Интервальная арифметика над конечным полем и ее приложения к теории экспериментов с автоматами
Об интервальном анализе
В интервальном анализе основным объектом исследования является интервал, представляющий собой замкнутый числовой промежуток. Так, интервал ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) содержит все вещественные числа, заключенные между границами интервала, включая и сами границы
содержит все вещественные числа, заключенные между границами интервала, включая и сами границы  и
и  . Когда говорят об интервальной неопределенности, подразумевают неполное знание о некоторой величине, т. е. невозможность указать ее точное значение, но возможность обозначить только границы ее изменения. Понятно, что ширина интервала есть мера неопределенности интересующей нас величины. Математическая теория, изучающая задачи с интервальными неопределенностями, получила название интервального анализа.
. Когда говорят об интервальной неопределенности, подразумевают неполное знание о некоторой величине, т. е. невозможность указать ее точное значение, но возможность обозначить только границы ее изменения. Понятно, что ширина интервала есть мера неопределенности интересующей нас величины. Математическая теория, изучающая задачи с интервальными неопределенностями, получила название интервального анализа.
Ясно, что арифметические операции над величинами, имеющими интервальную неопределенность, будут давать результаты, также содержащие интервальную неопределенность.
Методы интервального анализа [4] [26], развитые к настоящему времени, базируются на использовании арифметических операций с вещественными и комплексными числами. Эти методы находят применение в различных сферах. Так, они оказались полезными при решении многих практических задач, использующих в качестве переменных величины с интервальной неопределенностью.
Заметим, что источниками неопределенностей различных величин могут быть разнообразные факторы. В частности, таким источниками могут быть ограниченность разрядной сетки компьютера, ошибки различных преобразований, к примеру, преобразований чисел из одной системы счисления в другую, неточности измерений значений величин из-за естественного несовершенства измерительных приборов и т. п.
Необходимо отметить, что интервальный анализ - это не единственная теория, которая оперирует с величинами, содержащими неопределенности. Так, с подобного рода величинами имеют дело теории, использующие их размытые (нечеткие) или вероятностные описания. В связи с этим возникает естественный вопрос: имеет ли интервальный анализ какие-либо достоинства, которые отсутствуют, например, у теории вероятностей или теории нечетких множеств, нечетких графов и т. д.? Надо сказать, что такие достоинства у интервального анализа имеются. В частности, одно из них состоит в более высоком уровне развития математического аппарата для исследований. Так, ни в теории нечетких множеств, ни в теории вероятностей пока не достигнут тот качественный уровень методов решения систем уравнений с неопределенностями, который имеет место для интервальных систем уравнений.
Отметим также еще одно достоинство интервального анализа. Ранее все модели неопределенности, используемые при оценке параметров и идентификации, имели главным образом стохастический или вероятностный характер, базируясь на известных распределениях рассматриваемых величин и т. п. К сожалению, на практике часто бывает совершенно недостаточно информации, чтобы считать неопределенные факторы подчиняющимися какой-либо вероятностной модели, либо эти факторы не удовлетворяют тем или иным условиям, которые на них налагает вероятностная модель неопределенности. К примеру, таковыми могут быть условия независимости величин или специальный вид их распределения. С этой точки зрения интервальные неопределенности являются наименее ограничительными и более адекватны многим практическим задачам.
Укажем еще одну сферу применения интервального анализа - вычисления с приближенными числами, обеспечивающие достаточно точный учет ошибок округлений. Хорошо известно, что все современные компьютеры оперируют с числами, представленными в форме с плавающей запятой. Однако, к сожалению, они не вполне адекватны не только реальному физическому миру, но и его математическим моделям. Недостатками чисел с плавающей запятой является отсутствие информации о точности тех величин, которые они представляют. Недостатком их является невозможность представить многие используемые вещественные величины в виде чисел с конечной длиной мантиссы. Наконец, еще одним недостатком является отсутствие адекватности между свойствами арифметических операций над числами с плавающей запятой и свойствами идеальных арифметических операций над вещественными числами из-за ошибок округления.
Из сказанного следует, что вычисления с плавающей запятой не позволяют отслеживать вычислительных ошибок и потому не дают возможности произвести анализ точности результатов. Последнее чревато серьезными негативными последствиями при принятии критических решений на основе полученных приближенных результатов.
Обратимся теперь к рассматриваемым нами в курсе лекций линейным автоматам, задаваемым над конечным полем  . С физической точки зрения значения напряжений для входных и выходных сигналов, а также напряжений, которые связаны с представлениями сигналов в элементах памяти электронных устройств, описываемых моделями линейных автоматов, можно измерять в квантованных (калибровочных) единицах. Поскольку по техническим условиям значения напряжений имеют ограничения сверху, предельное значение этого напряжения, выраженное в квантованных единицах, можно принять в качестве характеристики p поля
. С физической точки зрения значения напряжений для входных и выходных сигналов, а также напряжений, которые связаны с представлениями сигналов в элементах памяти электронных устройств, описываемых моделями линейных автоматов, можно измерять в квантованных (калибровочных) единицах. Поскольку по техническим условиям значения напряжений имеют ограничения сверху, предельное значение этого напряжения, выраженное в квантованных единицах, можно принять в качестве характеристики p поля  . Такое постулирование приводит к необходимости оперировать с квантованными значениями напряжений, т. е. к вычислениям в арифметике по модулю р.
. Такое постулирование приводит к необходимости оперировать с квантованными значениями напряжений, т. е. к вычислениям в арифметике по модулю р.
Поскольку измерение значений входных и выходных сигналов из-за ограниченной точности измерительных приборов приводит к появлению интервалов, к которым принадлежат эти значения, возникает необходимость разработки фрагмента специфического интервального анализа. Основным объектом такого анализа является интервал с конечным числом элементов, границами которого являются элементы поля  . Заметим, что некоторые результаты такого анализа не имеют аналогов в интервальном анализе над вещественным полем
. Заметим, что некоторые результаты такого анализа не имеют аналогов в интервальном анализе над вещественным полем  .
.
Отметим, наконец, что на первый взгляд конечность поля  должна была бы привести к упрощению соответствующей арифметики, однако на самом деле произошло ее усложнение, что будет видно из результатов, изложенных в следующем разделе этой лекции.
должна была бы привести к упрощению соответствующей арифметики, однако на самом деле произошло ее усложнение, что будет видно из результатов, изложенных в следующем разделе этой лекции.
Рассмотренные в предыдущих лекциях синхронизирующие, установочные и диагностические эксперименты с линейными автоматами предполагали возможность получения в процессе их проведения точных значений реакций автоматов. Но, как уже упоминалось ранее, из-за несовершенства измерительных приборов более адекватным является предположение, что реакции автоматов представлены в интервальной форме. Понятно, что методы теории экспериментов, изложенные в предыдущих лекциях, не могут быть непосредственно применены для решения соответствующих задач в интервальной постановке. Однако их решение становится возможным с применением интервальной арифметики над полем  и специально разработанных для этих целей методов. В некоторых случаях такие методы являются аналогами "точных" методов, разработанных ранее, в иных же случаях "интервальные" методы таких аналогов не имеют. Таким образом, интервальная арифметика над конечным полем, о которой речь пойдет в следующем разделе этой лекции, нашла приложения в теории экспериментов с линейными автоматами в интервальной постановке.
и специально разработанных для этих целей методов. В некоторых случаях такие методы являются аналогами "точных" методов, разработанных ранее, в иных же случаях "интервальные" методы таких аналогов не имеют. Таким образом, интервальная арифметика над конечным полем, о которой речь пойдет в следующем разделе этой лекции, нашла приложения в теории экспериментов с линейными автоматами в интервальной постановке.
Интервальная арифметика над полем GF(p)
Начнем с обозначений и основных определений. Строчные греческие буквы 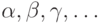 , а также латинские с чертой снизу или сверху
, а также латинские с чертой снизу или сверху 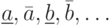 будут далее обозначать элементы поля
будут далее обозначать элементы поля 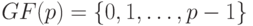 , где
, где  - простое число. Элемент этого поля представляет собой класс вычетов. Условимся далее считать, что каждый такой класс заменяется его представителем - наименьшим целым положительным числом, входящим в этот класс. На множестве классов вычетов определим отношения порядка
- простое число. Элемент этого поля представляет собой класс вычетов. Условимся далее считать, что каждый такой класс заменяется его представителем - наименьшим целым положительным числом, входящим в этот класс. На множестве классов вычетов определим отношения порядка  , которые естественным образом индуцируются соответствующими отношениями порядка на множестве целых чисел.
, которые естественным образом индуцируются соответствующими отношениями порядка на множестве целых чисел.
Подмножество 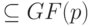 , такое, что
, такое, что ![a=[\underline a, \bar a]=\{\alpha \underline a \le \alpha \le \bar a; \underline a, \bar a \in GF(p)\}](/sites/default/files/tex_cache/ddbe5cc91a3566d158d85b2d5d6aad4f.png) будем называть правильным замкнутым интервалом, где
будем называть правильным замкнутым интервалом, где  и
и  - соответственно его нижняя и верхняя границы.
- соответственно его нижняя и верхняя границы.
Запись вида ![b=[\underline b, \bar b]](/sites/default/files/tex_cache/3dd44a6ddb308cc1643c719b5049f879.png) , где
, где  , будем интерпретировать как множество
, будем интерпретировать как множество ![GF(p)\ [\bar b+1, \underline b-1]](/sites/default/files/tex_cache/7d29a18fdf40b5d0980ff76b20d87b62.png) и называть это множество неправильным интервалом.
и называть это множество неправильным интервалом.
Интервал вида ![[\underline a, \bar a]](/sites/default/files/tex_cache/e0f747142066dd7da0419c9c8e529cd1.png) , где
, где  , будем называть вырожденным и интерпретировать его как элемент поля
, будем называть вырожденным и интерпретировать его как элемент поля  .
.
Множество всех интервалов над  обозначим через
обозначим через 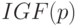 , а латинские буквы зарезервируем для обозначения интервалов.
, а латинские буквы зарезервируем для обозначения интервалов.
Исходя из интерпретации неправильного интервала ![[\underline b, \bar a]](/sites/default/files/tex_cache/b7544b7c24bff4ce1a64c43c5f04d3e0.png) как множества "внешних" элементов
как множества "внешних" элементов  по отношению к правильному интервалу
по отношению к правильному интервалу ![[\bar b+1, \underline b-1]](/sites/default/files/tex_cache/7bef95fe346191ee7b28b0fd1fdafef5.png) , любой неправильный интервал может быть представлен в следующем виде:
, любой неправильный интервал может быть представлен в следующем виде:
![[\underline b, \bar b]=[0, \bar b]\bigcup [\underline b, p-1]](/sites/default/files/tex_cache/4478be7065f83741be953c97089033ff.png) |
( 19.1) |
Определение 19.1. Два интервала ![a=[\underline a, \bar a]](/sites/default/files/tex_cache/3e7190bbb3501901640ba4f9c68e6273.png) и
и ![b=[\underline b, \bar b]](/sites/default/files/tex_cache/3dd44a6ddb308cc1643c719b5049f879.png) называются равными (и записывается это как
называются равными (и записывается это как 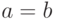 ), если они равны в смысле теории множеств.
), если они равны в смысле теории множеств.
Из этого определения следует, что 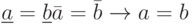 , но обратная импликация, в отличие от случая вещественных интервалов, места не имеет. Например, при
, но обратная импликация, в отличие от случая вещественных интервалов, места не имеет. Например, при  интервалы [2,1] и [3,2] равны как множества, однако их границы не совпадают. Легко видеть, что для любого
интервалы [2,1] и [3,2] равны как множества, однако их границы не совпадают. Легко видеть, что для любого  справедливо равенство
справедливо равенство ![[\alpha, \alpha-1]=[0,p-1]](/sites/default/files/tex_cache/fe1149b12c97cf2f08f42f71a099ba49.png)
Очевидно, что отношение равенства в 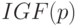 рефлексивно, симметрично и транзитивно.
рефлексивно, симметрично и транзитивно.
Введем операции над элементами 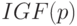 . Далее знаками +, -, ., / будем обозначать соответствующие арифметические операции над вещественными числами, а знаками
. Далее знаками +, -, ., / будем обозначать соответствующие арифметические операции над вещественными числами, а знаками 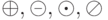 операции над элементами поля
операции над элементами поля  .
.
Определение 19.2. Пусть 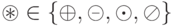 - бинарная арифметическая операция над элементами поля
- бинарная арифметическая операция над элементами поля  . Если
. Если 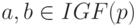 , то
, то
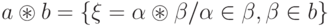 |
( 19.2) |
определяет бинарную арифметическую операцию над 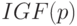 . (В случае деления предполагаем, что
. (В случае деления предполагаем, что 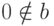 .)
.)
Очевидно, что операции сложения и умножения элементов 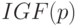 коммутативны.
коммутативны.
Если интерпретировать поле  как точки числовой оси, то каждый правильный интервал
как точки числовой оси, то каждый правильный интервал ![[\underline a, \bar a]](/sites/default/files/tex_cache/e0f747142066dd7da0419c9c8e529cd1.png) - это множество точек, расположенных вплотную одна за другой между
- это множество точек, расположенных вплотную одна за другой между  и
и  .
.
Отметим, что результатом операции над интервалом может оказаться множество точек, не являющихся одним интервалом, а представляющее собой объединение нескольких интервалов, разбросанных по числовой оси. Например, для ![p=7, [1,2]*[2,3]=[2,4]\bigsup [6,6]](/sites/default/files/tex_cache/a04a4882f19dae959ef81530ed4c93c6.png) .
.
Введем еще одно понятие. Подмножество  , такое, что
, такое, что
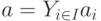 |
( 19.3) |
где 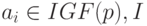 - конечное множество индексов и для
- конечное множество индексов и для  , назовем обобщенным интервалом поля
, назовем обобщенным интервалом поля 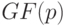 .
.
Обобщенный интервал будем обозначать строчной буквой. Понятно, что интервал из 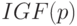 есть частный случай обобщенного интервала. За множеством всех обобщенных интервалов сохраним обозначение
есть частный случай обобщенного интервала. За множеством всех обобщенных интервалов сохраним обозначение 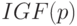 , поскольку из контекста каждый раз ясно, какой именно интервал имеется в виду в конкретном случае.
, поскольку из контекста каждый раз ясно, какой именно интервал имеется в виду в конкретном случае.
Введем бинарные операции над обобщенными интервалами.
Определение 19.3. Пусть 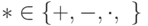 - бинарная операция. Если
- бинарная операция. Если
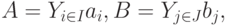
где  - обычные интервалы поля
- обычные интервалы поля  , то
, то

