Контроль функции выходов инициального автомата с использованием кратного безусловного эксперимента
Рассмотрим следующую задачу. Пусть в распоряжении экспериментатора есть несколько экземпляров автомата Мили  , у которого известны входной алфавит
, у которого известны входной алфавит  , выходной алфавит
, выходной алфавит 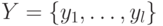 , множество состояний
, множество состояний  , где
, где  - выделенное состояние, называемое начальным, и функция переходов
- выделенное состояние, называемое начальным, и функция переходов 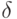 .Требуется построить кратный безусловный эксперимент, позволяющий распознать функцию выходов
.Требуется построить кратный безусловный эксперимент, позволяющий распознать функцию выходов 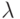 автомата
автомата  или эквивалентного ему автомата.
или эквивалентного ему автомата.
Легко видеть, что содержательный смысл этой задачи, в частности, соответствует также и контролю функции выходов инициального автомата кратным экспериментом.
Как и в "Эксперименты по контролю функции выходов инициального автомата" , мы обратимся к решению более общей задачи в рамках теории графов, а интересующие нас результаты будут получены как частные случаи.
Определение 8.1. Множество  путей в графе
путей в графе 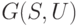 , исходящих из начальной вершины
, исходящих из начальной вершины  этого графа, назовем покрытием, если каждая дуга
этого графа, назовем покрытием, если каждая дуга 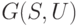 принадлежит некоторому пути из
принадлежит некоторому пути из  .
.
Определение 8.2. Число путей покрытия назовем его кратностью, а сумму длин всех путей покрытия - его длиной.
Перейдем к рассмотрению задачи построения покрытия графа 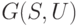 с начальной вершиной
с начальной вершиной  .
.
Ниже будут получены необходимые и достаточные условия разрешимости этой задачи, установлены достижимые оценки кратности и длины покрытия, предложен метод его построения.
Условимся считать, что из каждой вершины  графа
графа  исходит "пустой" путь нулевой длины, заканчивающийся в той же вершине. Будем говорить, что вершина
исходит "пустой" путь нулевой длины, заканчивающийся в той же вершине. Будем говорить, что вершина  графа
графа  достижима из вершины
достижима из вершины  , если в
, если в  существует путь из вершины
существует путь из вершины  в вершину
в вершину  . Из этого определения следует, что каждая вершина графа достижима из самой себя. Полагаем, что каждой вершине графа
. Из этого определения следует, что каждая вершина графа достижима из самой себя. Полагаем, что каждой вершине графа  инцидентна хотя бы одна дуга. Обозначим через
инцидентна хотя бы одна дуга. Обозначим через  множество всех тех вершин графа
множество всех тех вершин графа  , из которых исходит хотя бы одна дуга.
, из которых исходит хотя бы одна дуга.
Теорема 8.1. Покрытие графа  существует тогда и только тогда, когда любая вершина множества
существует тогда и только тогда, когда любая вершина множества  достижима из начальной.
достижима из начальной.
Доказательство. Пусть  - некоторое покрытие графа
- некоторое покрытие графа  и
и  - некоторая вершина из
- некоторая вершина из 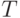 . Поскольку из вершины
. Поскольку из вершины  исходит некоторая дуга и эта дуга принадлежит одному из путей покрытия, то вершина
исходит некоторая дуга и эта дуга принадлежит одному из путей покрытия, то вершина  достижима из
достижима из  . Вершина
. Вершина  достижима из самой себя по крайней мере по "пустому" пути. Отсюда следует, что любая вершина множества
достижима из самой себя по крайней мере по "пустому" пути. Отсюда следует, что любая вершина множества 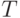 достижима из
достижима из  . Предположим теперь, что в графе
. Предположим теперь, что в графе  любая вершина
любая вершина  достижима из
достижима из  . Зафиксируем произвольно некоторую вершину
. Зафиксируем произвольно некоторую вершину 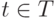 . Пусть
. Пусть 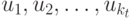 - путь, ведущий из
- путь, ведущий из  в
в  , а
, а  - множество всех дуг, исходящих из
- множество всех дуг, исходящих из  . Построим множество путей
. Построим множество путей 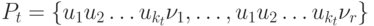 . Легко видеть, что объединение множеств
. Легко видеть, что объединение множеств  по всем
по всем 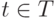 является покрытием графа
является покрытием графа  . Этим и заканчивается доказательство теоремы.
. Этим и заканчивается доказательство теоремы.
Граф, для которого существует покрытие, назовем правильным. Граф 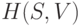 назовем сверхграфом графа
назовем сверхграфом графа 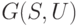 , если
, если 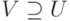 . Сверхграф
. Сверхграф  графа
графа  назовем регулярным, если любая дуга из множества
назовем регулярным, если любая дуга из множества 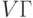 оканчивается в вершине
оканчивается в вершине  . Дуги этого множества будем называть замыкающими.
. Дуги этого множества будем называть замыкающими.
Лемма 8.1. Каждому контуру  регулярного сверхграфа
регулярного сверхграфа  графа
графа  , проходящему через все дуги графа
, проходящему через все дуги графа  , соответствует покрытие графа
, соответствует покрытие графа  .
.
Доказательство. Пусть  - контур, проходящий через все дуги регулярного сверхграфа
- контур, проходящий через все дуги регулярного сверхграфа  . По этому контуру строим множество
. По этому контуру строим множество  всех максимальных по длине путей, входящих в
всех максимальных по длине путей, входящих в  , но не содержащих замыкающих дуг. Поскольку каждая замыкающая дуга оканчивается в
, но не содержащих замыкающих дуг. Поскольку каждая замыкающая дуга оканчивается в  , то путь из
, то путь из  начинается в
начинается в  . Множество
. Множество  получено из контура
получено из контура  исключением только всех замыкающих дуг. Отсюда следует, что любая дуга графа
исключением только всех замыкающих дуг. Отсюда следует, что любая дуга графа  входит хотя бы в один путь из
входит хотя бы в один путь из  , т. е. есть покрытие.
, т. е. есть покрытие.
Лемма 8.2. Каждому покрытию графа  соответствует регулярный сильно связный сверхграф
соответствует регулярный сильно связный сверхграф  графа
графа  и контур
и контур  , проходящий через все дуги
, проходящий через все дуги  .
.
Доказательство. Пусть 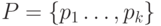 - покрытие графа
- покрытие графа  . По этому покрытию и графу
. По этому покрытию и графу  построим граф
построим граф  следующим образом: если путь
следующим образом: если путь  оканчивается в вершине
оканчивается в вершине  , то проведем из
, то проведем из  в
в  замыкающую дугу
замыкающую дугу 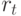 . Поскольку
. Поскольку  - правильный граф, то полученный граф
- правильный граф, то полученный граф 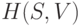 , где
, где 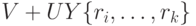 , является сильно связным регулярным сверхграфом графа
, является сильно связным регулярным сверхграфом графа  , а путь
, а путь 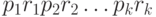 - контуром, проходящим через все дуги графа
- контуром, проходящим через все дуги графа  .
.
Определение 8.3. Покрытие 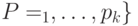 графа
графа  назовем приведенным, если выполняются следующие условия:
назовем приведенным, если выполняются следующие условия:
- для всех
 , путь
, путь 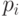 не является начальным отрезком пути
не является начальным отрезком пути 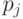 ;
; - для всякого
 , являющегося начальным отрезком пути
, являющегося начальным отрезком пути  , множество
, множество 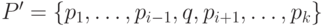 не является покрытием.
не является покрытием.
Пусть  - приведенное покрытие графа
- приведенное покрытие графа  . Из пункта 2 определения 8.3 следует, что если
. Из пункта 2 определения 8.3 следует, что если 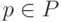 и
и  оканчивается дугой
оканчивается дугой  , то эта дуга не принадлежит никакому другому пути из
, то эта дуга не принадлежит никакому другому пути из  . Из последнего факта непосредственно вытекает, что для правильного графа
. Из последнего факта непосредственно вытекает, что для правильного графа  всегда существует приведенное покрытие, кратность которого не превосходит числа дуг графа. Легко видеть, что эта оценка достижима для графов с любым числом дуг и вершин. Из определения 8.3 также следует, что покрытие минимальной длины является приведенным.
всегда существует приведенное покрытие, кратность которого не превосходит числа дуг графа. Легко видеть, что эта оценка достижима для графов с любым числом дуг и вершин. Из определения 8.3 также следует, что покрытие минимальной длины является приведенным.
Если граф сильно связен, то всегда существует контур, проходящий через все его дуги, т. е. всегда существует приведенное покрытие этого графа кратности 1.
Рассмотрим теперь не сильно связный граф. Докажем ряд вспомогательных утверждений. Используемые обозначения те же, что и в лекции 6 ч. I.
Лемма 8.3. Для правильного не сильно связного графа множество положительных вершин не пусто.
Доказательство. Пусть  - некоторый правильный не сильно связный граф, у которого
- некоторый правильный не сильно связный граф, у которого 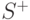 пусто. Тогда множество
пусто. Тогда множество 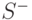 также пусто и, следовательно,
также пусто и, следовательно,  для всех
для всех  . Поскольку правильный граф связен, то из последнего факта следует, что граф
. Поскольку правильный граф связен, то из последнего факта следует, что граф  обладает эйлеровым контуром и, стало быть, он сильно связен. Полученное противоречие доказывает лемму.
обладает эйлеровым контуром и, стало быть, он сильно связен. Полученное противоречие доказывает лемму.
Лемма 8.4. Из любой вершины связного графа, у которого 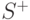 не пусто, достижима хотя бы одна положительная вершина.
не пусто, достижима хотя бы одна положительная вершина.
Доказательство. Пусть 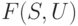 - связный граф, у которого
- связный граф, у которого 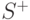 не пусто. Из каждой вершины
не пусто. Из каждой вершины 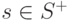 проведем ровно
проведем ровно  дуг, оканчивающихся в отрицательных вершинах, таким образом, чтобы каждая отрицательная вершина
дуг, оканчивающихся в отрицательных вершинах, таким образом, чтобы каждая отрицательная вершина  служила концом ровно
служила концом ровно 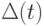 таких дуг.
таких дуг.
В результате получим новый граф 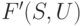 , у которого
, у которого 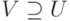 и для всех вершин
и для всех вершин 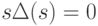 . В силу теоремы 2 из [25, c.182], граф
. В силу теоремы 2 из [25, c.182], граф 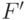 обладает эйлеровым контуром
обладает эйлеровым контуром  .
.
Рассмотрим отрезок этого контура, лежащий между двумя дугами из множества 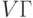 . Этот отрезок является, очевидно, путем, ведущим из некоторой отрицательной вершины графа
. Этот отрезок является, очевидно, путем, ведущим из некоторой отрицательной вершины графа  в некоторую положительную вершину. По построению графа
в некоторую положительную вершину. По построению графа 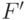 в каждую отрицательную вершину графа
в каждую отрицательную вершину графа  входит хотя бы одна дуга из
входит хотя бы одна дуга из 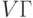 . Следовательно, из каждой отрицательной вершины графа
. Следовательно, из каждой отрицательной вершины графа  достижима некоторая положительная.
достижима некоторая положительная.
Любая положительная вершина достижима из самой себя по "пустому" пути. Рассмотрим, наконец, произвольную вершину  , у которой
, у которой  . Из нее достижима положительная вершина, поскольку из
. Из нее достижима положительная вершина, поскольку из  выходит по крайней мере одна дуга и эта дуга содержится в пути, порожденном контуром
выходит по крайней мере одна дуга и эта дуга содержится в пути, порожденном контуром  , из отрицательной в положительную вершину. Лемма доказана.
, из отрицательной в положительную вершину. Лемма доказана.
Рассмотрим граф  , множество
, множество 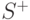 которого не пусто. Из каждой вершины
которого не пусто. Из каждой вершины 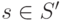 , где
, где 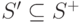 , проведем в вершину
, проведем в вершину  ровно
ровно  дуг. Эти дополнительные дуги обозначим через
дуг. Эти дополнительные дуги обозначим через  , где
, где  . Полученный граф обозначим через
. Полученный граф обозначим через 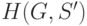 .
.
Теорема 8.2. Для правильного не сильно связного графа  всегда существует покрытие, кратность которого не превосходит величины
всегда существует покрытие, кратность которого не превосходит величины
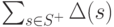 |
( 8.1) |
Доказательство. В силу леммы 8.3 множество 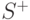 для правильного не сильно связного графа
для правильного не сильно связного графа  не пусто. Из теоремы 8.1 следует, что граф
не пусто. Из теоремы 8.1 следует, что граф  связен. Построим граф
связен. Построим граф 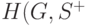 . В силу леммы 8.4 и правильности графа
. В силу леммы 8.4 и правильности графа  граф
граф 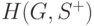 является сильно связным регулярным сверхграфом. Зафиксируем некоторый контур
является сильно связным регулярным сверхграфом. Зафиксируем некоторый контур  графа
графа 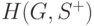 , проходящий через все его дуги. По лемме 8.1 этому контуру соответствует покрытие
, проходящий через все его дуги. По лемме 8.1 этому контуру соответствует покрытие  , содержащее пути, полученные из
, содержащее пути, полученные из  исключением всех замыкающих дуг
исключением всех замыкающих дуг 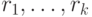 графа
графа 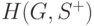 . Из правила построения этого графа следует, что между любыми двумя вхождениями замыкающих дуг в контуре
. Из правила построения этого графа следует, что между любыми двумя вхождениями замыкающих дуг в контуре  имеется хотя бы одна дуга графа
имеется хотя бы одна дуга графа  . Для завершения доказательства теоремы достаточно показать, что в графе
. Для завершения доказательства теоремы достаточно показать, что в графе 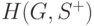 существует такой контур
существует такой контур  , проходящий через все дуги этого графа, что каждая дуга
, проходящий через все дуги этого графа, что каждая дуга 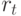 входит в этот контур только один раз. По построению в графе
входит в этот контур только один раз. По построению в графе 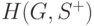 для каждой вершины
для каждой вершины  и положительной может быть только вершина
и положительной может быть только вершина  . Поскольку из
. Поскольку из  достижима любая вершина графа, то всегда можно построить компенсирующую систему графа
достижима любая вершина графа, то всегда можно построить компенсирующую систему графа 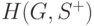 , используя только дуги из
, используя только дуги из 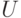 . Следовательно, искомый контур
. Следовательно, искомый контур  существует. По лемме 8.1 ему соответствует покрытие кратности (8.1), что и требовалось доказать.
существует. По лемме 8.1 ему соответствует покрытие кратности (8.1), что и требовалось доказать.
Легко видеть, что оценка (8.1) достижима для всех ее значений.
Оценим снизу кратность покрытия правильного графа  . Напомним, что множество
. Напомним, что множество 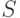 состоит из вершин графа
состоит из вершин графа  , из которых не выходят дуги. По ранее сделанному предположению любая вершина графа
, из которых не выходят дуги. По ранее сделанному предположению любая вершина графа  инцидентна хотя бы одной дуге, но тогда
инцидентна хотя бы одной дуге, но тогда 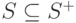 . Пусть мощность множества
. Пусть мощность множества 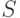 равна
равна 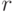 . По лемме 8.2 всякому покрытию графа
. По лемме 8.2 всякому покрытию графа  соответствует некоторый регулярный сильно связный сверхграф
соответствует некоторый регулярный сильно связный сверхграф  графа
графа  , число замыкающих дуг которого не меньше
, число замыкающих дуг которого не меньше 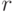 . Отсюда следует, что кратность любого покрытия графа
. Отсюда следует, что кратность любого покрытия графа  не может быть меньше величины
не может быть меньше величины 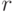 . Легко видеть, что эта оценка достижима для всех значений
. Легко видеть, что эта оценка достижима для всех значений 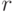 .
.
Перейдем к уточнению нижней оценки кратности. Множество 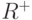 вершин графа
вершин графа  определим следующим образом:
определим следующим образом: 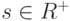 , если
, если 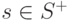 и из вершины
и из вершины  не достижима ни одна отрицательная вершина графа
не достижима ни одна отрицательная вершина графа  . Очевидно, что
. Очевидно, что 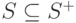 и для правильного графа
и для правильного графа 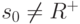 . Кроме того, для правильного не сильно связного графа
. Кроме того, для правильного не сильно связного графа  множество
множество 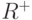 не пусто. Доказательство этого утверждения может быть проведено по аналогии с доказательством леммы 8.3.
не пусто. Доказательство этого утверждения может быть проведено по аналогии с доказательством леммы 8.3.
Покажем справедливость следующего утверждения.
Теорема 8.3. Кратность покрытия правильного графа не может быть меньше величины
 |
( 8.2) |
Доказательство. Пусть 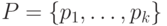 - некоторое покрытие графа
- некоторое покрытие графа  . По этому покрытию, используя доказательство леммы 8.3, построим сильно связный регулярный сверхграф
. По этому покрытию, используя доказательство леммы 8.3, построим сильно связный регулярный сверхграф  графа
графа  . Пусть
. Пусть  - контур графа
- контур графа  , соответствующий покрытию
, соответствующий покрытию  . Каждую дугу графа
. Каждую дугу графа  заменим дугами
заменим дугами  с тем же началом и концом, где
с тем же началом и концом, где  - число вхождений дуги в контур. Полученный в результате граф
- число вхождений дуги в контур. Полученный в результате граф 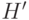 обладает эйлеровым контуром. Поскольку для любой вершины
обладает эйлеровым контуром. Поскольку для любой вершины  графа
графа 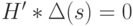 , то в вершину
, то в вершину  заходит не менее
заходит не менее 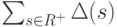 замыкающих дуг. Таким образом, кратность покрытия графа
замыкающих дуг. Таким образом, кратность покрытия графа  не может быть меньше величины (8.2).
не может быть меньше величины (8.2).
Рассмотрим граф, изображенный на рис.8.1. Для этого графа 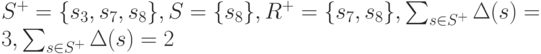 .
.
Множество  является, очевидно, приведенным покрытием кратности 2, т. е. оценка (8.2) в данном примере достижима. Нетрудно показать, что (8.2) является достижимой для любого своего значения.
является, очевидно, приведенным покрытием кратности 2, т. е. оценка (8.2) в данном примере достижима. Нетрудно показать, что (8.2) является достижимой для любого своего значения.
Следствие 1. Если для правильного не сильно связного графа  множества
множества 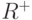 и
и 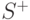 совпадают, то минимальная кратность покрытия графа
совпадают, то минимальная кратность покрытия графа  равна величине (8.1).
равна величине (8.1).
Справедливость этого утверждения вытекает непосредственно из теорем 8.2, 8.3 и того факта, что при совпадении множеств 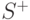 и
и 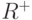 оценки (8.1) и (8.2) равны.
оценки (8.1) и (8.2) равны.

