Эксперименты в пространстве обобщенных состояний и с линейными автоматами с запаздыванием
Эксперименты с линейными автоматами в пространстве обобщенных состояний
Наряду с традиционным понятием состояния ЛА  размерности
размерности  , представляющего собой
, представляющего собой  -мерный вектор, введем понятие обобщенного состояния. С этой целью зафиксируем некоторое целое положительное число
-мерный вектор, введем понятие обобщенного состояния. С этой целью зафиксируем некоторое целое положительное число  , такое, что
, такое, что  , и вектор-столбец
, и вектор-столбец
 |
( 12.1) |
где  - символ неопределенности, будем называть обобщенным состоянием (ОС) линейного автомата. Предполагается, что каждый символ неопределенности
- символ неопределенности, будем называть обобщенным состоянием (ОС) линейного автомата. Предполагается, что каждый символ неопределенности  может принимать любое значение из поля
может принимать любое значение из поля 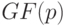 . Таким образом, каждому ОС линейного автомата соответствует некоторое подмножество
. Таким образом, каждому ОС линейного автомата соответствует некоторое подмножество 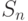 всех состояний ЛА. Далее через
всех состояний ЛА. Далее через  будем обозначать пространство обобщенных состояний ЛА. Понятно, что число обобщенных состояний в
будем обозначать пространство обобщенных состояний ЛА. Понятно, что число обобщенных состояний в  равно
равно  .
.
Вообще говоря, обобщенное состояние ЛА можно определить иначе, например, положив
![\tilde s(t)=[s_1(t), \dots, s_{i_1-1}(t), \dots, x, s_{i_1+1}(t), \dots, s_{i_{n- \mu -1}}(t_, x, s_{i_{n- \mu +1}}(t), \dots, s_n(t)]'](/sites/default/files/tex_cache/8083c46bddec238aa81b57117ca045e8.png) |
( 12.2) |
где  штук значений координат
штук значений координат 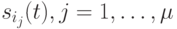 , номера которых выбраны произвольным образом, замещены символом неопределенности
, номера которых выбраны произвольным образом, замещены символом неопределенности  . Легко показать, что путем подходящих перестановок строк и столбцов характеристических матриц линейный автомат
. Легко показать, что путем подходящих перестановок строк и столбцов характеристических матриц линейный автомат  всегда может быть преобразован в такой изоморфный ему ЛА
всегда может быть преобразован в такой изоморфный ему ЛА  , у которого ОС (12.2) отображается при этом в ОС (12.1). Поэтому для простоты записи, но не теряя при этом общности, примем первый вариант (12.1) определения ОС.
, у которого ОС (12.2) отображается при этом в ОС (12.1). Поэтому для простоты записи, но не теряя при этом общности, примем первый вариант (12.1) определения ОС.
Далее условимся о следующих обозначениях: если  есть матрица, то через
есть матрица, то через ![[H]_a](/sites/default/files/tex_cache/929bfd29bdfe3cc16422f759d916f78e.png) обозначим матрицу с
обозначим матрицу с  штук строками, совпадающими с первыми
штук строками, совпадающими с первыми  строками матрицы
строками матрицы  . Аналогичное обозначение используем и для вектора:
. Аналогичное обозначение используем и для вектора: ![[\bar s]_a](/sites/default/files/tex_cache/57abfc0d72c6d9b5673bdd772b669e92.png) - это вектор размерности
- это вектор размерности  , у которого координаты совпадают с
, у которого координаты совпадают с  первыми координатами вектора
первыми координатами вектора  .
.
ЛА с заданной величиной  , определяющей для ЛА пространство обобщенных состояний, условимся обозначать как
, определяющей для ЛА пространство обобщенных состояний, условимся обозначать как  -ЛА.
-ЛА.
Введем для  -ЛА понятие обобщенной диаграммы переходов (ОДП). ОДП для
-ЛА понятие обобщенной диаграммы переходов (ОДП). ОДП для  -ЛА над полем
-ЛА над полем 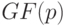 назовем ориентированный граф, содержащий
назовем ориентированный граф, содержащий  вершин, взаимно однозначно соответствующих каждому ОС этого автомата. Две вершины
вершин, взаимно однозначно соответствующих каждому ОС этого автомата. Две вершины  и
и  в ОДП соединяются дугой, ведущей из
в ОДП соединяются дугой, ведущей из  в
в  , помеченной входным символом
, помеченной входным символом 
 -ЛА, если существуют по крайней мере два таких "традиционных" состояния
-ЛА, если существуют по крайней мере два таких "традиционных" состояния  и
и  из
из 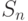 , что
, что ![[s]_{\mu}=\bar a, [s]_{\mu}=\bar b, \tilde s=A\bar s+B\bar u](/sites/default/files/tex_cache/a9a6c86b7b789991bf4edf5cd8f7dba2.png) .
.
Отметим различие между "традиционной" диаграммой переходов ЛА [19] и ОДП: в "традиционной" диаграмме каждой ее дуге, помеченной входным символом 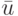 , соответствует единственный выходной символ (реакция ЛА на вход
, соответствует единственный выходной символ (реакция ЛА на вход 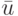 в состоянии
в состоянии  ), а в ОДП некоторой дуге может соответствовать несколько выходных символов. Назовем ОДП сильно связной, если в ней для любой пары вершин
), а в ОДП некоторой дуге может соответствовать несколько выходных символов. Назовем ОДП сильно связной, если в ней для любой пары вершин  и
и  существует путь, ведущий из
существует путь, ведущий из  в
в  . Соответствующий этой ОДП
. Соответствующий этой ОДП  -ЛА будем называть
-ЛА будем называть  -сильно связным.
-сильно связным.
Понятно, что любому пути в ОДП из  в
в  соответствует некоторое входное слово
соответствует некоторое входное слово  -ЛА, возможно не одно, переводящее его из ОС
-ЛА, возможно не одно, переводящее его из ОС  в ОС
в ОС  .
.
По аналогии с [19]  -ЛА назовем
-ЛА назовем  -управляемым, если для любых двух его обобщенных состояний
-управляемым, если для любых двух его обобщенных состояний  и
и  существует входное слово длины
существует входное слово длины  , переводящее его из
, переводящее его из  в
в  . Очевидно, что
. Очевидно, что  -управляемый
-управляемый  -ЛА является
-ЛА является  -сильно связным.
-сильно связным.
Теорема 12.1.  -ЛА является
-ЛА является  -управляемым тогда и только тогда, когда ранг матрицы
-управляемым тогда и только тогда, когда ранг матрицы
![[L_k]_{\mu}=[A^{k-1}B, A^{k-2}B, \dots, AB,B]_{\mu}](/sites/default/files/tex_cache/a20140084277d21300a762102f45d091.png)
равен  .
.
Доказательство. Пусть ![[\bar s]_{\mu}](/sites/default/files/tex_cache/072740c1875cc18d8ed6bde1fe82e92b.png) и
и ![[\tilde s]_{\mu}](/sites/default/files/tex_cache/930279c10e7bc7454a90cc0ef0f9519c.png) - различные произвольные ОС рассматриваемого
- различные произвольные ОС рассматриваемого  -ЛА. По определению
-ЛА. По определению  -управляемости существует такая входная последовательность
-управляемости существует такая входная последовательность  длины
длины  , которая переводит
, которая переводит  -ЛА из
-ЛА из ![[\bar s]_{\mu}](/sites/default/files/tex_cache/072740c1875cc18d8ed6bde1fe82e92b.png) в
в ![[\tilde s]_{\mu}](/sites/default/files/tex_cache/930279c10e7bc7454a90cc0ef0f9519c.png) . Тогда на основании формулы (1.3) можно записать:
. Тогда на основании формулы (1.3) можно записать:
![[\bar s]_{\mu}=[A^k \tilde s+A^{k-1}B\bar u(0)+\dots |AB\bar u(k-2)+B\bar u(k-1)]_{\mu}](/sites/default/files/tex_cache/14fb8740061136b6e650e2895f2aa734.png)
Отсюда следует, что
![[\bar s-A^k\tilde s]_{\mu}=[A^{k-1}B\bar u(0)+ \dots +AB\bar u(k-2)+b\bar u(k-1)]_{\mu}=\\
=[L_k[\bar u(0), \bar u(1), \dots, \bar u(k-1)]']_{\mu}](/sites/default/files/tex_cache/fc8364106e11636a1f7f33edf84ee59e.png)
Поскольку 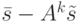 может быть любым
может быть любым  -мерным вектором,
-мерным вектором, ![[\bar s-A^k\tilde s]_{\mu}](/sites/default/files/tex_cache/273b946f4d217bed19866a7982fc67aa.png) также может быть любым
также может быть любым  -мерным вектором. В силу этого последнее равенство можно записать в виде
-мерным вектором. В силу этого последнее равенство можно записать в виде
![[L_k \hat u]_{\mu}](/sites/default/files/tex_cache/bcb6ad570e29caacec8b28580c5df8f8.png) |
( 12.3) |
где ![\hat u=[\bar u(0), \bar u(1), \dots, \bar u(k-1)]'](/sites/default/files/tex_cache/b3f77766a8cb30a32b8d5346f39c4f8c.png) , и интерпретировать его как СЛАУ относительно неизвестных, являющихся координатами вектора
, и интерпретировать его как СЛАУ относительно неизвестных, являющихся координатами вектора  .
.
Понятно, что существование входной последовательности, переводящей  -ЛА из произвольного ОС
-ЛА из произвольного ОС ![[\tilde s]_{\mu}](/sites/default/files/tex_cache/930279c10e7bc7454a90cc0ef0f9519c.png) в произвольное ОС
в произвольное ОС ![[\bar s]_{\mu}](/sites/default/files/tex_cache/072740c1875cc18d8ed6bde1fe82e92b.png) , эквивалентно существованию решений выписанной выше системы при любых правых частях. Из алгебры известно [33], что необходимым и достаточным условием для этого является равенство ранга системы (12.3) величине
, эквивалентно существованию решений выписанной выше системы при любых правых частях. Из алгебры известно [33], что необходимым и достаточным условием для этого является равенство ранга системы (12.3) величине  . Заметим, что при
. Заметим, что при  , где
, где  - размерность ЛА,
- размерность ЛА,  -сильно связность совпадает с общепринятым понятием сильно связности ЛА. Очевидно, что если ЛА размерности
-сильно связность совпадает с общепринятым понятием сильно связности ЛА. Очевидно, что если ЛА размерности  является сильно связным, то он будет
является сильно связным, то он будет  -сильно связным при любом
-сильно связным при любом  . Обратное, однако, в общем случае неверно. Действительно, рассмотрим ЛА над полем
. Обратное, однако, в общем случае неверно. Действительно, рассмотрим ЛА над полем 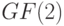 , заданный характеристическими матрицами
, заданный характеристическими матрицами
![A=
\left [
\begin {matrix}
0&1&0\\
1&0&\\
0&0&1
\end {matrix}
\right ],
B=
\left [
\begin {matrix}
0\\
1\\
1
\end {matrix}
\right ]](/sites/default/files/tex_cache/530576c132e5991579cd50ab22dd05b9.png)
Путем вычислений можно убедиться, что
![L_3=[A^2B,AB,B]=
\left [
\begin {matrix}
0&1&0\\
1&0&1\\
1&1&1
\end {matrix}
\right ]](/sites/default/files/tex_cache/06f01ccc0270542928c21305f2c8abb6.png)
и 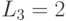 . Тогда по теореме 12.1 этот ЛА не является сильно связным.
. Тогда по теореме 12.1 этот ЛА не является сильно связным.
Положим 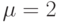 , тогда
, тогда
![[L_3]_2=
\left [
\begin {matrix}
0&1&0\\
1&0&1
\end {matrix}
\right ]](/sites/default/files/tex_cache/6f57577060c7c9101b70e55f02dc4ecf.png)
и ![rank [L_3]_2=2](/sites/default/files/tex_cache/de53fd6b6a5d4366543f27256c8b17a6.png) . По теореме 12.1 рассматриваемый
. По теореме 12.1 рассматриваемый  -ЛА является 2-сильно связным. Таким образом, исходный ЛА не является сильно связным, однако в пространстве обобщенных состояний он становится 2-сильно связным.
-ЛА является 2-сильно связным. Таким образом, исходный ЛА не является сильно связным, однако в пространстве обобщенных состояний он становится 2-сильно связным.
Определим теперь понятие синхронизирующей последовательности для  -ЛА в пространстве обобщенных состояний.
-ЛА в пространстве обобщенных состояний.
Входную последовательность 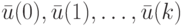
 -ЛА назовем обобщенной СП (ОСП), если
-ЛА назовем обобщенной СП (ОСП), если
![\forall \bar s, \tilde s \in \tilde {S_{\mu}}\ \ [A^{k+1}\bar S+A^kB\bar u(0)+ \dots +B\bar u(k)]_{\mu}=[A^{k+1}\tilde s +A^kB \bar u(0)+ \dots +B \bar u(k)]_{\mu}](/sites/default/files/tex_cache/f0e9a8295bdd0946ec325e8df6d3490b.png) |
( 12.4) |
Понятно, что при  , где
, где  - размерность ЛА, приведенное определение совпадает с определением обычной СП для этого же автомата. Перенося в (12.4) правую часть равенства влево и выполнив сокращения, получим
- размерность ЛА, приведенное определение совпадает с определением обычной СП для этого же автомата. Перенося в (12.4) правую часть равенства влево и выполнив сокращения, получим
![\forall \bar s, \tilde s \in S_{\mu}\ \
[A^{k+1}\bar s - A^k \tilde s)]_{\mu}=[0]_{\mu}](/sites/default/files/tex_cache/beab12a8d073655de545d24e3e00c012.png) |
( 12.5) |
где ![[0]=_{\mu}](/sites/default/files/tex_cache/80818c84575ba0ceeebae2ccaed9a769.png) - нулевой вектор размерности
- нулевой вектор размерности  . Поскольку в (12.5)
. Поскольку в (12.5)  и
и  могут быть любыми ОС из
могут быть любыми ОС из  , то (12.5) эквивалентно
, то (12.5) эквивалентно
![\forall \bar s \in S_n\ \
[A^{k+1}\bar s]_{\mu}=[0]_{\mu}](/sites/default/files/tex_cache/b3c9bd51e77393ccf473f7794dd64e84.png) |
( 12.6) |
Из предиката (12.6) вытекает справедливость следующего утверждения.
Теорема 12.2. Для того чтобы  -ЛА
-ЛА  имела ОСП длины
имела ОСП длины  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
![[A^{k+1}]_{\mu}=[0]_{\mu}](/sites/default/files/tex_cache/9216a9e070a39612c0ba4d67b42c8514.png)
Как видим, эта теорема является аналогом теоремы 1.1 для обычного ЛА, т. е. ее естественным обобщением.
По аналогии с разделом 1.2  -ЛА условимся называть обобщенно синхронизируемым, если для него существует ОСП.
-ЛА условимся называть обобщенно синхронизируемым, если для него существует ОСП.
Рассмотрим ЛА над полем 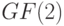 , заданный следующими характеристическими матрицами:
, заданный следующими характеристическими матрицами:
![A=
\left [
\begin {matrix}
0&0&0\\
0&1&0\\
0&0&1
\end {matrix}
\right ],
B=
\left [
\begin {matrix}
0\\
0\\
0
\end {matrix}
\right ]](/sites/default/files/tex_cache/d875c6c778b524f6a6a65d3aa57acee2.png)
Поскольку ![A \ne [0]](/sites/default/files/tex_cache/f95b6ab60bbfd4f9eaa01b88e21d89e6.png) , то для этого ЛА, как это следует из теоремы 1.1, СП длины 1 не существует. Положим
, то для этого ЛА, как это следует из теоремы 1.1, СП длины 1 не существует. Положим  и рассмотрим соответствующий 1-ЛА. Понятно, что состояние этого автомата в момент времени
и рассмотрим соответствующий 1-ЛА. Понятно, что состояние этого автомата в момент времени  не зависит от состояния в момент
не зависит от состояния в момент  , так как
, так как  есть нулевая матрица. Более того, для этого ЛА
есть нулевая матрица. Более того, для этого ЛА
![s(t+1)=[0 s_2(t) s_2(t)]'](/sites/default/files/tex_cache/a821b96017b014bc19637685de3bfb0a.png)
Из последнего равенства следует, что
![[s(t+1)]_1=[0]_1](/sites/default/files/tex_cache/17714738cbd06088128f07b7dceb59dd.png)
Последнее означает: любая входная последовательность длины 1 переводит 1-ЛА в одно и то же состояние ![[0]_1](/sites/default/files/tex_cache/aa16fbb1f726727f1df983e32a907eec.png) , т. е. любая такая последовательность является ОСП.
, т. е. любая такая последовательность является ОСП.
Таким образом, нами построен пример ЛА, не имеющего обычной СП некоторой фиксированной длины, но в то же время имеющего обобщенную СП такой длины.
Почти дословное повторение доказательства теоремы 1.2 позволяет установить справедливость ее аналога для  -ЛА.
-ЛА.
Теорема 12.3. Если для  -ЛА существует хотя бы одна ОСП длины
-ЛА существует хотя бы одна ОСП длины  , то обобщенными СП для него являются любые входные последовательности длины
, то обобщенными СП для него являются любые входные последовательности длины  и более.
и более.
По аналогии с обобщенными СП введем понятия обобщенных УП и ДП для  -ЛА
-ЛА  , полагая, что множеством его допустимых начальных состояний является множество, которое мы обозначим как
, полагая, что множеством его допустимых начальных состояний является множество, которое мы обозначим как 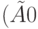 .
.
Входную последовательность 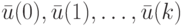
 -ЛА
-ЛА  назовем обобщенной УП (ОУП), если
назовем обобщенной УП (ОУП), если
![\forall \bar s(0), \tilde s(0) \in Init(\tilde A) \wedge_{d=0}^k[CA^d\bar s(0)+CA^{d-1}B\bar u(0)+ \dots +CB \bar u(d-1)+D\bar u(d)=\\
= CA^d \tilde s(0)+CA^{d-1}B\bar u(0)+ \dots +CB\bar u(d-1)+D\bar u(d)] \to\\
\to [A^{k+1}\bar s(0)+A^kB\bar u(0)+ \dots +AB\bar u(k-1)+B\bar u(k)]_{\mu}=\\
=[A^{k+1}\tilde s(0)+A^kB\bar u(0)+ \dots +AB\bar u(k-1)+B\bar u(k)]_{\mu}](/sites/default/files/tex_cache/5b16da57679d5ab46378dde341a9d991.png)
Входную последовательность 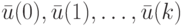
 -ЛА
-ЛА  назовем обобщенной ДП (ОДП), если
назовем обобщенной ДП (ОДП), если
![\forall \bar s(0), \tilde s(0) \in Init (\tilde A) \wedge_{d=0}^k[CA^d\bar s(0)+CA^{d-1}B\bar u(0)+ \dots +CB\bar u(d-1)+D\bar u(d)=\\
=CA^d \tilde s())+CA^{d-1}B\bar u(0)+ \dots + CB\bar u(d-1)+D\bar u(d)] \to [\bar s(0)]_{\mu}=[\tilde s(0)]_{\mu}](/sites/default/files/tex_cache/5f4e0cfac5d59e8f2a1ac62c915bd093.png)
Заметим, что содержательный смысл обобщенных УП и ДП тот же, что и обычных, но применительно к обобщенным состояниям. Ниже приводятся теоремы, которые содержат естественные обобщения результатов для обычных ЛА на ЛА, рассматриваемые в пространстве обобщенных состояний. Доказательства некоторых из этих утверждений опущены, поскольку могут быть получены за счет незначительного изменения уже приводившихся ранее доказательств.
Теорема 12.4. Для того чтобы  -ЛА имел обобщенную УП длины
-ЛА имел обобщенную УП длины  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
![\forall \bar s \in \hat {Init}(\tilde A) (\exists k \ge 0 CA^k\bar s \ne [0]) \vee (\exists k \ge 0 [A^{k+1}\bar s]_{\mu}=[0]_{\mu})](/sites/default/files/tex_cache/96318f387fe1699b1f19f608587c7e4d.png)
Здесь через  обозначено множество состояний, представляющее собой всевозможные разности состояний из множества
обозначено множество состояний, представляющее собой всевозможные разности состояний из множества  .
.
Теорема 12.5. Если у  -ЛА
-ЛА  размерности
размерности  ранг характеристической матрицы
ранг характеристической матрицы  равен
равен  , то для него существует обобщенная УП длины 1.
, то для него существует обобщенная УП длины 1.
Доказательство. Пусть  и
и  - два различных начальных состояния
- два различных начальных состояния  -ЛА
-ЛА  из множества допустимых. Через
из множества допустимых. Через  и
и  обозначим реакции этого автомата на входной символ
обозначим реакции этого автомата на входной символ  . Пусть
. Пусть ![[\bar {s_k}]_{\mu}](/sites/default/files/tex_cache/b809b82749d26fcf59d5e37de7e60b37.png) и
и ![[\tilde {s_k}]_{\mu}](/sites/default/files/tex_cache/d71524a997632780af71822437d21392.png) - состояния
- состояния  -ЛА после подачи
-ЛА после подачи  . Если
. Если  - обобщенная УП, то это означает, что
- обобщенная УП, то это означает, что
![\forall \bar s, \tilde s \in \Init (\tilde A) \bar y(0)=\tilde y(0) \to [\bar {s_k}]_{\mu}=[\bar {s_k}]_{\mu}](/sites/default/files/tex_cache/89f8346e663b6cfd4b5ba92907bea317.png)
Предположим, что  не является обобщенной УП, тогда
не является обобщенной УП, тогда
![\exists \bar s, \tilde s \in \Init (\tilde A) \bar y(0)=\tilde y(0) \wedge [\bar {s_k}]_{\mu} \ne [\bar {s_k}]_{\mu}](/sites/default/files/tex_cache/0c3b82910dbc2a049647961d1a09c28e.png)
что эквивалентно
![\exists \bar s, \tilde s \in \Init (\tilde A) C(\bar s - \tilde s)=[0] \wedge [\bar {s_k}]_{\mu} \ne [\bar {s_k}]_{\mu}](/sites/default/files/tex_cache/716017f4a5f57e3166bd219bcfdc4136.png) |
( 12.7) |
Первый сомножитель в (12.7) можно интерпретировать как систему линейных однородных уравнений относительно  неизвестных, являющихся координатами вектор-состояния. Эта система должна иметь ненулевое решение, поскольку по предположению
неизвестных, являющихся координатами вектор-состояния. Эта система должна иметь ненулевое решение, поскольку по предположению  . Из алгебры известно, что необходимым и достаточным условием для этого является выполнение неравенства
. Из алгебры известно, что необходимым и достаточным условием для этого является выполнение неравенства

что противоречит условию теоремы. Отсюда следует ложность предиката (12.7) и, следовательно, справедливость теоремы.
Теорема 12.6. Если для  -ЛА размерности
-ЛА размерности  существует хотя бы одна обобщенная УП длины
существует хотя бы одна обобщенная УП длины  , то для этого автомата обобщенными УП являются любые входные последовательности длины
, то для этого автомата обобщенными УП являются любые входные последовательности длины  и более.
и более.
Введем следующие обозначения: через  и
и 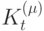 соответственно обозначим подматрицы матрицы
соответственно обозначим подматрицы матрицы
![K_t=[C, CA, \dots, CA^{t-1}]'](/sites/default/files/tex_cache/71c7f7f0c03fe7ac4cabd0da5987902e.png)
содержащие первые и соответственно последние  ее столбцов.
ее столбцов.
Теорема 12.7. Для того чтобы  -ЛА
-ЛА  размерности
размерности  имел обобщенную ДП длины
имел обобщенную ДП длины  , необходимо и достаточно, чтобы ранг матрицы
, необходимо и достаточно, чтобы ранг матрицы  был равен
был равен  и
и ![K_t^{(\mu)}=[0]](/sites/default/files/tex_cache/20a50167b1aea3bd006a463f5af37a54.png) .
.
Эта теорема является естественным обобщением теоремы 1.7. Два последующих утверждения являются аналогами теорем 1.8 и 1.9.
Теорема 12.8. Если для  -ЛА существует хотя бы одна обобщенная ДП длины
-ЛА существует хотя бы одна обобщенная ДП длины  , то для него обобщенными являются любые входные последовательности длины
, то для него обобщенными являются любые входные последовательности длины  и более.
и более.
Теорема 12.9. Если для  -ЛА размерности
-ЛА размерности  существуют обобщенные ДП, то длина таких минимальных последовательностей не превосходит
существуют обобщенные ДП, то длина таких минимальных последовательностей не превосходит  .
.
Заметим, что аналоги последней теоремы справедливы как для обобщенных СП, так и для обобщенных УП.
