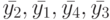Установочные и диагностические эксперименты со стационарными и нестационарными линейными автоматами
Условия существования установочной последовательности
Сформулированное ранее определение УП для автомата Мили применительно к линейному автомату принимает следующий вид: входную последовательность 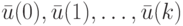 ЛА
ЛА  назовем УП, если
назовем УП, если
![\forall \bar s(0), \hat s(0) \in S_n \wedge_{d=0}^{k}[CA^d \bar s (0)+CA^{d-1} B \bar u(0)+ \dots +CB \bar u (d-1)+D \bar u(d)=\\
=CA^d \hat s(0)+CA^{d-1}B \bar u(0)+ \dots CB \bar u(d-1)+D \bar u(d)] \to\\
\to [A^{k+1} \bar s(0)+A^kB \baru(0)+ \dots +AB \bar u(k-1)+B \bar u(k)=\\
=A^{k+1} \hat s(0)+A^kB \bar u(0)+ \dots +AB \bar u(k-1)+B \bar u(k)](/sites/default/files/tex_cache/3715fe658422ce9a0b6df8792b3e0cf1.png) |
( 11.1) |
Знак 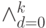 в (11.1) означает конъюнкцию
в (11.1) означает конъюнкцию  выражений, стоящих после этого знака и получаемых при изменении индекса
выражений, стоящих после этого знака и получаемых при изменении индекса 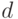 от 0 до
от 0 до  .
.
Отметим также, что допустимое множество состояний ЛА при построении УП предполагается совпадающим со всем множеством 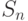 состояний ЛА.
состояний ЛА.
Теорема 11.1. Для ЛА А УП длины k+1 существует тогда и только тогда, когда
![(\forall \bar s \in S_n \vee_{d=0}^k CA^d \bar s \ne [0]) \vee A^{k+1}=[0]](/sites/default/files/tex_cache/fc2a10a87e100bfac634a429332653bf.png) |
( 11.2) |
Доказательство. Вначале отметим, что знак 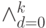 в (11.2) означает дизъюнкцию
в (11.2) означает дизъюнкцию 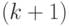 выражений и имеет аналогичный со знаком
выражений и имеет аналогичный со знаком 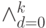 в (11.1) смысл.
в (11.1) смысл.
Преобразуем (11.1), перенеся в левую часть обоих равенств все слагаемые, участвующие в них, и произведем соответствующие сокращения:
![\forall \bar s(0), \hat s(0) \in S_n \wedge{d=0}^k(CA^d(\bar s(0)- \hat s(0))=[0]) \to A^{k+1}(\bar s(0)-\hat s(0)=[0]](/sites/default/files/tex_cache/5f646dbb0e03042ace7489148f3d640c.png)
Используя известный факт, что высказывание  равносильно
равносильно 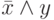 , получаем, что последний предикат эквивалентен следующему:
, получаем, что последний предикат эквивалентен следующему:
![\forall \bar s(0), \hat s(0) \in S_n \wedge_{d=0}^k(CA^d(\bar s(0)-\hat s(0)) \ne [0]) \wedge A^{k+1}(\bar s(0)- \hat s(0))=[0]](/sites/default/files/tex_cache/186a90673af520d423f75c07e951d4a6.png) |
( 11.3) |
Поскольку  и
и 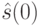 - произвольные состояния из
- произвольные состояния из 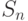 , то очевидно, что
, то очевидно, что  пробегает все состояния из
пробегает все состояния из 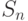 . Тогда равенство
. Тогда равенство ![A^{k+1}(\bar s(0)-\hat s(0)=[0]](/sites/default/files/tex_cache/0f4b446f11fa1f0855da013572c5c36b.png) равносильно равенству
равносильно равенству ![A^{k+1}=[0]](/sites/default/files/tex_cache/8cce1fe954269072ef2325ffeedd04b8.png) и, следовательно, предикат (1.20) эквивалентен предикату
и, следовательно, предикат (1.20) эквивалентен предикату
![\forall \bar s \in S_n \left ( \wedge_{d=0}^k CA^d \bar s \ne [0] \right ) \wedge A^{k+1}=[0]](/sites/default/files/tex_cache/b4b4cfc9082db52e0e10a835914d8443.png)
Теорема 11.2. Если для ЛА 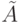 , у которого характеристическая матрица
, у которого характеристическая матрица  невырожденная, существует хотя бы одна УП длины
невырожденная, существует хотя бы одна УП длины  , то для этого автомата установочными являются любые входные последовательности длины
, то для этого автомата установочными являются любые входные последовательности длины  и более.
и более.
Доказательство. Напомним, что аналогичное утверждение относительно синхронизирующих последовательностей, являющихся частным случаем УП, было доказано выше. Поэтому теорему 11.2 достаточно доказать для собственно установочных последовательностей, не являющихся СП.
Доказательство проведем от противного. Предположим, что некоторая последовательность p длины  является УП, но наряду с ней существует последовательность
является УП, но наряду с ней существует последовательность 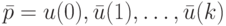 той же длины, которая для рассматриваемого ЛА установочной последовательностью не является. Это означает, что у ЛА существует два таких различных состояния
той же длины, которая для рассматриваемого ЛА установочной последовательностью не является. Это означает, что у ЛА существует два таких различных состояния  и
и  , что, стартуя в них, он выдает одинаковые выходные реакции
, что, стартуя в них, он выдает одинаковые выходные реакции  , но переходит в различные конечные состояния
, но переходит в различные конечные состояния 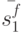 и
и  . Выпишем реакции и конечные состояния ЛА, соответствующие различным начальным состояниям.
. Выпишем реакции и конечные состояния ЛА, соответствующие различным начальным состояниям.
 |
( 11.4) |
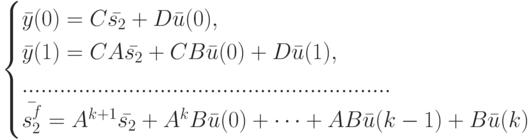 |
( 11.5) |
Учитывая, что  , из (11.4) и (11.5) получаем
, из (11.4) и (11.5) получаем
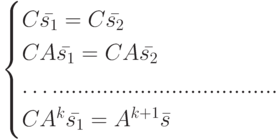 |
( 11.6) |
Последнее равенство в (11.6) равносильно
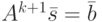 |
( 11.7) |
где ![\bar s \ne [0]](/sites/default/files/tex_cache/05aa6eab76dfd4d2e90f099408fea930.png) и
и ![\bar b \ne [0]](/sites/default/files/tex_cache/5b66a4b1d59c06ef6e6dd5a98a952967.png) .
.
Соотношение (11.7) можно интерпретировать как матричную форму записи системы линейных неоднородных уравнений относительно неизвестных, являющихся координатами вектор-столбца 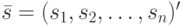 . Поскольку эта система имеет ненулевое решение
. Поскольку эта система имеет ненулевое решение  , тогда, как известно из алгебры [33], ее определитель
, тогда, как известно из алгебры [33], ее определитель  . В силу того, что
. В силу того, что 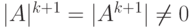 , определитель
, определитель 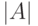 также отличен от нуля, т. е. матрица
также отличен от нуля, т. е. матрица  невырожденная. Отсюда вытекает, что для нее существует обратная матрица
невырожденная. Отсюда вытекает, что для нее существует обратная матрица 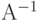 , также невырожденная. Умножая слева последнее неравенство в (11.6) на
, также невырожденная. Умножая слева последнее неравенство в (11.6) на 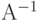 , получим
, получим

где матрица  - невырожденная. Поскольку по условию теоремы матрица
- невырожденная. Поскольку по условию теоремы матрица  невырожденная, умножив на нее обе части последнего неравенства, получим
невырожденная, умножив на нее обе части последнего неравенства, получим
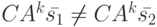
что противоречит предпоследнему равенству в (11.6). Полученное противоречие доказывает теорему.
Доказанная теорема говорит о принципиальном различии между автоматами Мили и линейными автоматами с точки зрения идентификации их конечных состояний с помощью УП. В общем случае, если автоматы Мили имеют УП длины  , то число таких последовательностей меньше числа всех последовательностей этой же длины. В то же время для ЛА, заданного над полем
, то число таких последовательностей меньше числа всех последовательностей этой же длины. В то же время для ЛА, заданного над полем 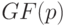 , как утверждает теорема, существование одной УП длины
, как утверждает теорема, существование одной УП длины  влечет существование
влечет существование 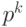 таких УП.
таких УП.
Таким образом, для ЛА задача построение УП фактически сводится к задаче нахождения такого натурального числа  , при котором УП длины
, при котором УП длины  существует. В то же время для автоматов Мили в общем случае задача построения УП далеко не тривиальна и требует применения специально разработанных для этого методов.
существует. В то же время для автоматов Мили в общем случае задача построения УП далеко не тривиальна и требует применения специально разработанных для этого методов.
Заметим, что поиск целого числа  , являющегося длиной минимальной УП для ЛА, осуществляется точно так же, как и поиск длины минимальной СП, что было описано в предыдущем разделе.
, являющегося длиной минимальной УП для ЛА, осуществляется точно так же, как и поиск длины минимальной СП, что было описано в предыдущем разделе.
Для иллюстрации теоремы 11.2 рассмотрим ЛА над полем GF(2), заданный следующими характеристическими матрицами:
![A=
\left [
\begin {matrix}
1&1\\
1&0
\end {matrix}
\right ] ,\\
B=
\left [
\begin {matrix}
0&1\\
0&0
\end {matrix}
\right ] ,\\
C=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ],\\
D=
\left [
\begin {matrix}
0&0\\
0&1
\end {matrix}
\right ]](/sites/default/files/tex_cache/6b3278d4c45f7b457439f5dc266d6d65.png)
Обозначим состояния этого ЛА через ![\bar {s_1}=[0,0]', \bar {s_2}=[0,1]', \bar {s_3}=[1,0]', \bar {s_4}=[1,1]'](/sites/default/files/tex_cache/574a547a6ad07423818c39cf06e07617.png) и его выходные реакции через
и его выходные реакции через ![\bar {y_1}=[0,0]', \bar {y_2}=[0,1]', \bar {y_3}=[1,0]', \bar {y_4}=[1,1]'](/sites/default/files/tex_cache/4870ffa5c8426cb884f69680b2290770.png) .
.
Заметим, что рассматриваемый ЛА не имеет СП, поскольку его основная характеристическая матрица  невырожденная. Приведенная ниже таблица показывает, что для этого ЛА УП являются все входные последовательности длины 1.
невырожденная. Приведенная ниже таблица показывает, что для этого ЛА УП являются все входные последовательности длины 1.
Теорема 11.3. Если для  -мерного ЛА существуют УП, то минимальная их длина не превосходит величины
-мерного ЛА существуют УП, то минимальная их длина не превосходит величины  .
.
Доказательство. В [19] доказано следующее утверждение: ![CA^k \bar s=[0]](/sites/default/files/tex_cache/89fe99627f4790183c594f39474bdac9.png) для любого
для любого  тогда и только тогда, когда
тогда и только тогда, когда ![K \bar s=[0]](/sites/default/files/tex_cache/2569e02e5cd2239a9bed5fb75d23d8cf.png) , где диагностическая матрица
, где диагностическая матрица
![K=
\left [
\begin {matrix}
C\\
CA\\
CA^2\\
…..\\
CA^{n-1}
\end {matrix}
\right ]](/sites/default/files/tex_cache/b2e4760ebb7dd568fa72271ea144fba7.png)
Очевидно, что это равносильно следующему предикату:
![\exists k \ge CA^k \bar s \ne [0] \leftrightarrow K \bar s \ne [0]](/sites/default/files/tex_cache/3782d677b0f02b9cb7f4de996e9041d1.png) |
( 11.8) |
Последнее утверждение фактически обосновывает достаточность проверки равенства ![CA^k \bar s=[0]](/sites/default/files/tex_cache/89fe99627f4790183c594f39474bdac9.png) только для
только для 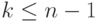 . Если при этих значениях
. Если при этих значениях ![k CA^k \bar s=[0]](/sites/default/files/tex_cache/ff55cc57cf48fa095444d4347af90ba3.png) , то и при
, то и при  это равенство также остается справедливым. Отсюда и вытекает справедливость теоремы.
это равенство также остается справедливым. Отсюда и вытекает справедливость теоремы.
Заметим, что поскольку СП для ЛА является частными случаями УП, то приведенная в теореме 10.6 верхняя оценка длины УП является одновременно и верхней оценкой длины для СП.
Условия существования диагностической последовательности
Теорема 11.4. Для того чтобы  -мерный ЛА
-мерный ЛА  имел ДП длины
имел ДП длины  , необходимо и достаточно, чтобы ранг матрицы
, необходимо и достаточно, чтобы ранг матрицы
![K_t=
\left [
\begin {matrix}
C\\
CA\\
CA^2\\
…..\\
CA^{t-1}
\end {matrix}
\right ]](/sites/default/files/tex_cache/c5d7bb1227a4c219c7a61677fb1fb994.png)
был равен n.
Доказательство. Выпишем реакции ЛА  , стартующего в неизвестном начальном состоянии
, стартующего в неизвестном начальном состоянии  , на входную последовательность
, на входную последовательность 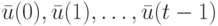 длины
длины  :
:
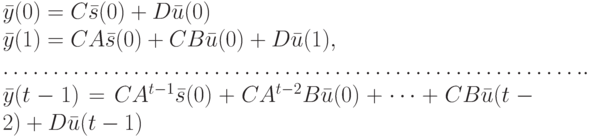
Простыми и очевидными преобразованиями эти равенства всегда можно привести к виду
![C\bar s(0)=[Z_0],\\
CA\bar s(0)=[Z_1],\\
…………………..\\
CA^{t-1}\bar s(0)=[Z_{t-1}]](/sites/default/files/tex_cache/967cec46c5c076a2c66f657d37a01336.png) |
( 11.9) |
где ![[Z_i], i=1,2,\dots, t-1](/sites/default/files/tex_cache/1f7368dbe4131cf74855160ed31f1ec8.png) - некоторые конкретные вектор-столбцы размерности
- некоторые конкретные вектор-столбцы размерности  , где
, где  - число выходов ЛА.
- число выходов ЛА.
Существование ДП длины  для рассматриваемого ЛА
для рассматриваемого ЛА  означает, что СЛАУ (11.9) относительно неизвестных
означает, что СЛАУ (11.9) относительно неизвестных 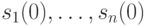 , являющихся координатами вектора
, являющихся координатами вектора  , должна иметь единственное решение, которое и соответствует искомому начальному состоянию ЛА. Из алгебры известно, что СЛАУ обладает единственным решением тогда и только тогда, когда ранг этой системы равен числу неизвестных. Отсюда вытекает справедливость теоремы.
, должна иметь единственное решение, которое и соответствует искомому начальному состоянию ЛА. Из алгебры известно, что СЛАУ обладает единственным решением тогда и только тогда, когда ранг этой системы равен числу неизвестных. Отсюда вытекает справедливость теоремы.
Теорема 11.5. Если у ЛА существует хотя бы одна ДП длины  , то для этого ЛА диагностическими являются любые входные последовательности длины
, то для этого ЛА диагностическими являются любые входные последовательности длины  и более.
и более.
Справедливость этой теоремы вытекает из того, что матрица 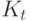 , фигурирующая в теореме 11.4, не зависит от входных слов.
, фигурирующая в теореме 11.4, не зависит от входных слов.
Что касается процедуры поиска минимального значения  , при котором для заданного ЛА существует ДП, то она полностью совпадает с процедурой поиска минимальной длины СП и УП, описанной выше.
, при котором для заданного ЛА существует ДП, то она полностью совпадает с процедурой поиска минимальной длины СП и УП, описанной выше.
Теорема 11.6. Если для  -мерного ЛА существует ДП, то минимальная их длина не превышает величины
-мерного ЛА существует ДП, то минимальная их длина не превышает величины  .
.
Справедливость этой теоремы следует из того, что каждая ДП является одновременно и УП, а для УП такая верхняя оценка установлена в предыдущем подразделе.
В [18] было установлено, что в общем случае минимальность автомата Мили является необходимым, но не достаточным условием существования для него ДП. Покажем, что для ЛА имеет место следующее утверждение.
Теорема 11.7. Если ЛА минимален, то у него существует ДП.
Доказательство. Проведем его в предположении, что множество всех состояний 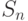 ЛА и множество его допустимых начальных состояний совпадают.
ЛА и множество его допустимых начальных состояний совпадают.
Напомним, что в [19] была доказана справедливость следующего утверждения: состояния  и
и  ЛА эквивалентны тогда и только тогда, когда
ЛА эквивалентны тогда и только тогда, когда  . С учетом этого утверждения минимальность ЛА означает
. С учетом этого утверждения минимальность ЛА означает

Последнее означает, что СЛАУ ![K \bar s =[0]](/sites/default/files/tex_cache/619bb4f079b1356959ffe87e4ac84f47.png) в случае минимальности ЛА должна иметь только нулевые решения. Из алгебры известно, что это выполняется только тогда, когда ранг матрицы
в случае минимальности ЛА должна иметь только нулевые решения. Из алгебры известно, что это выполняется только тогда, когда ранг матрицы 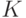 системы равен
системы равен  , т. е. числу неизвестных этой системы. Отсюда в силу теоремы 11.4 вытекает справедливость доказываемой теоремы.
, т. е. числу неизвестных этой системы. Отсюда в силу теоремы 11.4 вытекает справедливость доказываемой теоремы.
Отыскание ДП для заданного ЛА обычно называют диагностической задачей. Известно [18], что возможность решения диагностической задачи для автомата Мили зависит от множества его допустимых начальных состояний, а также от применяемых для этого средств. В [18] показано, что наиболее мощным средством для решения диагностических задач являются кратные эксперименты, меньшими возможностями обладают простые безусловные эксперименты. Ниже будет показано, что для линейных автоматов упомянутая иерархия разрешающих возможностей перечисленных типов экспериментов не существует.
Теорема 11.8. Для любого минимального ЛА и любого множества его допустимых начальных состояний диагностическая задача всегда разрешима с помощью простого безусловного диагностического эксперимента.
Доказательство. Пусть у минимального ЛА множество допустимых начальных состояний совпадает со всем множеством его состояний. Напомним, что автомат называется определенно диагностируемым, если существует такое натуральное число  , что все входные последовательности длины
, что все входные последовательности длины  являются для него диагностическими. Из теоремы 11.5 следует, что любой ЛА является определенно диагностируемым. Покажем, что любое входное слово длины
являются для него диагностическими. Из теоремы 11.5 следует, что любой ЛА является определенно диагностируемым. Покажем, что любое входное слово длины  , где
, где  - размерность ЛА, различает любые два состояния минимального ЛА. Предположим противное. Пусть существуют два таких состояния ЛА, которые не различаются некоторым словом длины
- размерность ЛА, различает любые два состояния минимального ЛА. Предположим противное. Пусть существуют два таких состояния ЛА, которые не различаются некоторым словом длины  . С учетом теоремы 11.6 это означает, что рассматриваемый минимальный ЛА не является определенно диагностируемым, что противоречит теореме 11.5. Полученное противоречие доказывает наше утверждение.
. С учетом теоремы 11.6 это означает, что рассматриваемый минимальный ЛА не является определенно диагностируемым, что противоречит теореме 11.5. Полученное противоречие доказывает наше утверждение.
Эта теорема фактически означает, что простой безусловный эксперимент с ЛА обладает большими возможностями, чем аналогичный эксперимент с автоматом Мили, поскольку, как известно из [18], в последнем случае диагностическая задача разрешима не для всякого множества допустимых начальных состояний, мощность которого более двух.
Обратимся теперь к простым условным диагностическим экспериментам. Известно [18], что для автоматов Мили существуют диагностические задачи для множества допустимых начальных состояний более чем с двумя элементами, которые не разрешимы простым безусловным, но разрешимы простым условным экспериментом. Из теоремы 11.8 следует, что такая ситуация не может иметь места для минимальных ЛА. Другими словами, все диагностические задачи, разрешимые простыми условными экспериментами, могут быть разрешены и простыми безусловными. Таким образом, для ЛА разрешающие возможности обоих типов диагностических экспериментов просто совпадают.
Остановимся теперь на кратных диагностических экспериментах. В [18] доказано, что для любого автомата диагностическая задача для произвольного множества допустимых начальных состояний всегда разрешима кратным безусловным экспериментом. Тогда, как это следует из теоремы 11.8, для минимальных ЛА разрешающие возможности кратного безусловного и простого экспериментов совпадают.
Подведем итог: для минимальных ЛА ни простые условные, ни кратные безусловные диагностические эксперименты не привносят ничего нового по сравнению с простыми безусловными диагностическими экспериментами с точки зрения принципиальной возможности решения диагностических задач.
Сделанный вывод, однако, не означает, что условные и кратные диагностические эксперименты являются бесполезными средствами при решении диагностических задач. Нетрудно построить такие примеры диагностических задач, решения которых с помощью условных и кратных экспериментов достигаются последовательностями меньшей длины по сравнению с длиной безусловного эксперимента.

![\left [
\begin {matrix}
0\\
0
\end {matrix}
\right ]](/sites/default/files/tex_cache/c1ec3317d34d4bacbeff271176ad1216.png)
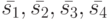

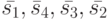
![\left [
\begin {matrix}
0\\
1
\end {matrix}
\right ]](/sites/default/files/tex_cache/377ecfb3c2404943926a38ecf242e7e0.png)

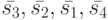
![\left [
\begin {matrix}
1\\
0
\end {matrix}
\right ]](/sites/default/files/tex_cache/be685388f5787c709c1c3917b1c544b6.png)
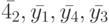
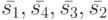
![\left [
\begin {matrix}
1\\
1
\end {matrix}
\right ]](/sites/default/files/tex_cache/f7482ea70db50e7f81fbef2000a0a658.png)