Обобщенные автоматы без потери информации
Автоматы, рассматриваемые как преобразователи информации, используются в системах передачи сообщений и выполняют различные функции, в том числе кодирования этих сообщений. В последней ситуации принятое получателем закодированное сообщение должно быть однозначно декодировано. В этой главе рассматриваются автоматы, удовлетворяющие этому требованию.
Основополагающие работы в области исследования автоматов, являющихся моделями таких устройств, принадлежат Д. Хаффмену [76] и С. Ивену [74]. В этих работах введены и изучены два класса автоматов, названных соответственно автоматами без потери информации (БПИ-автоматами) и автоматами без потери информации конечного порядка (БПИК-автоматами), которые позволяют однозначно декодировать принятое сообщение. В упомянутых работах исследуемые автоматы предполагались инициальными, т. е. стартующими из известного начального состояния.
В этой лекции предложены обобщения БПИ- и БПИК-автоматов в двух направлениях. Одно из них связано с отказом от предположения об их инициальности, а второе - с исследованием такого рода автоматов со структурированными входными и выходными алфавитами. В последней ситуации восстановление неизвестных входных последовательностей осуществляется не в полном объеме, а на заданном подмножестве компонент структурированного входного символа.
В этом разделе в качестве математической модели ДУ используется слабоинициальный автомат Мили 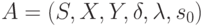 , где
, где  - множество его допустимых начальных состояний, причем
- множество его допустимых начальных состояний, причем 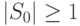 . Далее предполагается, что входной и выходной алфавиты автомата являются структурированными, т. е.
. Далее предполагается, что входной и выходной алфавиты автомата являются структурированными, т. е. 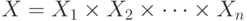 и
и 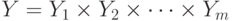 .
.
Пусть 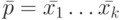 - последовательность входных символов (входное слово) автомата
- последовательность входных символов (входное слово) автомата  . Число
. Число  назовем длиной слова
назовем длиной слова 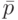 .
.
Пусть 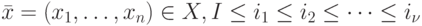 , - натуральные числа,
, - натуральные числа, 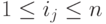 , тогда проекцией
, тогда проекцией 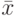 по каналам с номерами
по каналам с номерами 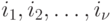 назовем вектор
назовем вектор 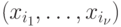 и будем обозначать ее
и будем обозначать ее  , а проекцией слова
, а проекцией слова 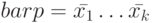 по тем же каналам назовем упорядоченную последовательность
по тем же каналам назовем упорядоченную последовательность 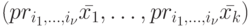 и будем обозначать ее
и будем обозначать ее 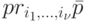 .
.
Рассмотрим следующую задачу. На автомат  , находящийся в одном из состояний множества
, находящийся в одном из состояний множества  , но неизвестно, в каком именно, подается неизвестное входное слово
, но неизвестно, в каком именно, подается неизвестное входное слово 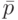 , и наблюдается реакция автомата на это слово по выходным каналам с номерами
, и наблюдается реакция автомата на это слово по выходным каналам с номерами  , где
, где 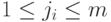 . Требуется построить эксперимент, проводимый с автоматом
. Требуется построить эксперимент, проводимый с автоматом  после приложения слова
после приложения слова 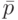 , позволяющий распознать проекцию этого слова по каналам с номерами
, позволяющий распознать проекцию этого слова по каналам с номерами 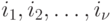 , где
, где 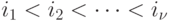 .
.
Автоматы, для которых сформулированная задача может быть решена независимо от входного слова 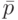 и действительного начального состояния из множества
и действительного начального состояния из множества  , назовем обобщенными автоматами без потери информации (ОБПИ-автоматами).
, назовем обобщенными автоматами без потери информации (ОБПИ-автоматами).
Далее, не теряя общности, положим, что 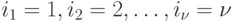 и соответственно
и соответственно  , т. е. реакция автомата
, т. е. реакция автомата  на слово
на слово 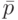 наблюдается по первым
наблюдается по первым  выходным каналам, а в каждом символе
выходным каналам, а в каждом символе 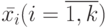 слова
слова 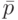 восстановлению подлежат сигналы, поступающие на автомат по первым
восстановлению подлежат сигналы, поступающие на автомат по первым  входным каналам.
входным каналам.
Из формулировки задачи следует, что ОБПИ-автоматы должны обладать следующим свойством:
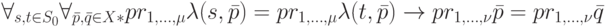 |
( 3.1) |
Отметим, что определенные нами ОБПИ-автоматы в качестве частного случая включают в себя ранее известные БПИ-автоматы, введенные Д. Хаффменом [76], и автоматы существенно без потери информации (СБПИ-автоматы) [9] [43], введенные автором предлагаемой монографии. БПИ-автоматы получаются при 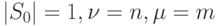 , а СБПИ-автоматы получаются при
, а СБПИ-автоматы получаются при  .
.
Определение 3.1. Пару состояний  и
и  автомата
автомата  назовем состояниями с потерей информации (СПИ-состояниями), если
назовем состояниями с потерей информации (СПИ-состояниями), если
 |
( 3.2) |
Заметим, что если 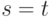 , то приведенное определение совпадает с определением из [76], и в этом случае
, то приведенное определение совпадает с определением из [76], и в этом случае  называется СПИ-состоянием.
называется СПИ-состоянием.
Теорема 3.1. Для того чтобы автомат  был ОБПИ-автоматом, необходимо и достаточно, чтобы он не имел СПИ-состояний.
был ОБПИ-автоматом, необходимо и достаточно, чтобы он не имел СПИ-состояний.
Доказательство. Необходимость условий теоремы очевидна, покажем их достаточность.
Пусть условия теоремы выполняются. Предположим, что на вход автомата  было подано неизвестное слово
было подано неизвестное слово  , а на первых
, а на первых  выходных каналах наблюдалось слово
выходных каналах наблюдалось слово  . По таблице переходов-выходов автомата
. По таблице переходов-выходов автомата  определим пары "состояние - входное слово"
определим пары "состояние - входное слово"  , такие, что
, такие, что  и
и  , где
, где 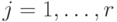 . Понятно, что среди слов
. Понятно, что среди слов 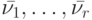 находится и искомое слово.
находится и искомое слово.
Пусть  . Покажем, что между парами
. Покажем, что между парами 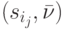 и состояниями
и состояниями 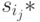 существует взаимно однозначное соответствие. Последнее означает, что такое соответствие существует и между
существует взаимно однозначное соответствие. Последнее означает, что такое соответствие существует и между  и состояниями
и состояниями 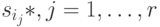 .
.
Если все состояния  попарно различны, справедливость сформулированного утверждения очевидна. Предположим, что среди состояний
попарно различны, справедливость сформулированного утверждения очевидна. Предположим, что среди состояний  имеется по крайней мере два совпадающих. Без ограничения общности можно считать, что
имеется по крайней мере два совпадающих. Без ограничения общности можно считать, что  . Из последнего равенства следует, что
. Из последнего равенства следует, что 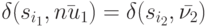 . По построению пары
. По построению пары  и
и 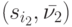 различны, что возможно только в следующих трех случаях:
различны, что возможно только в следующих трех случаях:
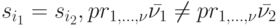
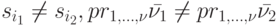
-
 .
.
В первом случае состояние 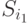 является по определению СПИ-состоянием, что противоречит нашему предположению. Во втором случае пара состояний
является по определению СПИ-состоянием, что противоречит нашему предположению. Во втором случае пара состояний 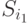 и
и  является по определению СПИ-состояниями, что также противоречит нашему предположению. Таким образом, в действительности может иметь место только третий случай, когда у двух входных слов
является по определению СПИ-состояниями, что также противоречит нашему предположению. Таким образом, в действительности может иметь место только третий случай, когда у двух входных слов  и
и  их проекции по каналам
их проекции по каналам 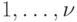 совпадают. Это и доказывает справедливость утверждения о существовании взаимно однозначного соответствия между
совпадают. Это и доказывает справедливость утверждения о существовании взаимно однозначного соответствия между  и состояниями
и состояниями 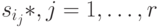 .
.
Продолжим доказательство теоремы. Предположим, что среди состояний  все попарно различные состояния образуют множество
все попарно различные состояния образуют множество 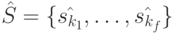 , где
, где  . Рассматривая
. Рассматривая 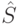 в качестве множества допустимых начальных состояний автомата
в качестве множества допустимых начальных состояний автомата  , построим для него установочную последовательность
, построим для него установочную последовательность  . Обозначим через
. Обозначим через  состояние, в которое перейдет автомат
состояние, в которое перейдет автомат  после подачи слова
после подачи слова  , а выходную последовательность, которую он выдает при этом, обозначим через
, а выходную последовательность, которую он выдает при этом, обозначим через  . Если пара
. Если пара  порождается только из одного состояния множества
порождается только из одного состояния множества 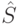 (этот факт легко установить по таблице переходов-выходов автомата
(этот факт легко установить по таблице переходов-выходов автомата  ), тогда, очевидно, существует взаимно однозначное соответствие между заключительным состоянием
), тогда, очевидно, существует взаимно однозначное соответствие между заключительным состоянием  и состоянием
и состоянием 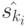 , между
, между 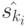 и
и 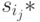 и, наконец, между
и, наконец, между 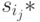 и
и 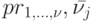 . В силу сказанного, знание заключительного состояния
. В силу сказанного, знание заключительного состояния  позволяет однозначно восстановить проекцию неизвестного входного слова, поданного на автомат
позволяет однозначно восстановить проекцию неизвестного входного слова, поданного на автомат  , по каналам с номерами
, по каналам с номерами 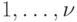 .
.
Если пара  порождается из двух различных состояний множества
порождается из двух различных состояний множества 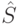 , например
, например  и
и 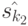 , то им взаимно однозначно соответствуют состояния
, то им взаимно однозначно соответствуют состояния  и
и 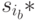 , последним - состояния
, последним - состояния 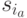 и
и 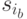 из множества
из множества  , а состояниям
, а состояниям 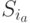 и
и  , в свою очередь, взаимно однозначно соответствуют входные слова
, в свою очередь, взаимно однозначно соответствуют входные слова 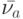 и
и 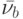 . В силу выполненных выше построений имеем следующие равенства:
. В силу выполненных выше построений имеем следующие равенства:
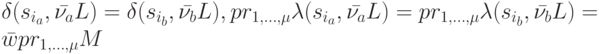
Если входные слова 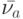 и
и 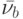 таковы, что
таковы, что  , то искомая проекция восстанавливается однозначно. Если же выписанные только что проекции различны, то это означает, что пара состояний
, то искомая проекция восстанавливается однозначно. Если же выписанные только что проекции различны, то это означает, что пара состояний 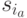 и
и 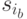 является СПИ-состояниями. Этот факт противоречит условию теоремы.
является СПИ-состояниями. Этот факт противоречит условию теоремы.
Заметим, что аналогичные рассуждения справедливы и для случая, когда пара  порождается более чем из двух состояний.
порождается более чем из двух состояний.
Теорема доказана.
Доказательство теоремы фактически содержит алгоритм распознавания проекции неизвестного входного слова по заданному множеству каналов, который сформулируем в явном виде.
- Наблюдаем проекцию
 выходного слова автомата
выходного слова автомата  по каналам
по каналам 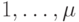 , являющуюся реакцией на подачу неизвестного входного слова
, являющуюся реакцией на подачу неизвестного входного слова  . По таблице переходов-выходов автомата
. По таблице переходов-выходов автомата  определяем все пары "состояние - входное слово"
определяем все пары "состояние - входное слово"  , такие, что
, такие, что  и
и 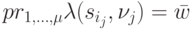 , где
, где 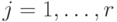 .
. - Строим установочную последовательность
 , считая множеством
, считая множеством 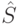 допустимых начальных состояний автомата множество всех попарно различных состояний из совокупности состояний
допустимых начальных состояний автомата множество всех попарно различных состояний из совокупности состояний 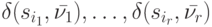 .
. - Подаем на вход автомата
 слово
слово  и наблюдаем выходное слово
и наблюдаем выходное слово  . По паре
. По паре  определяем заключительное состояние автомата
определяем заключительное состояние автомата  и все те состояния
и все те состояния  , которые этой парой порождаются.
, которые этой парой порождаются.
Из множества пар  выделяем все те его элементы, для которых
выделяем все те его элементы, для которых  . Если этот элемент один, то проекция второго члена выделенной пары по каналам
. Если этот элемент один, то проекция второго члена выделенной пары по каналам 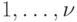 и есть искомое входное слово. Если число таких элементов больше двух, то у них упомянутые проекции вторых членов пар совпадают и являются искомым входным словом.
и есть искомое входное слово. Если число таких элементов больше двух, то у них упомянутые проекции вторых членов пар совпадают и являются искомым входным словом.
Рассмотрим пример. Пусть ОБПИ-автомат задан графом на рис.3.1. Условимся, что для наблюдения реакции выделен 1-й выходной канал автомата (по нему выдается левый символ выходной пары) и проекция неизвестного входного слова восстанавливается по 1-му входному каналу, т. е. 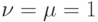 . Пусть
. Пусть 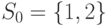 , на автомат подано неизвестное входное слово длиной 3, а по 1-му выходному каналу при этом наблюдалась реакция 0,1,1. Строим последовательность пар "состояние - входное слово", упомянутую в пункте 1 алгоритма: (1;10,00,10), (1;10,00,11), (1;10,00,00), (1;10,00,11), (1;10,01,10), (1;10,01,11), (1;10,01,00), (1;10,01,10), (1;11,00,10), (1;11,00,11), (1;11,00,00), (1;11,00,10), (1;11,01,10), (1;11,01,11), (1;11,01,00), (1;11,01,10), (2;10,10,10), (2;10,10,11), (2;10,11,10), (2;10,11,11), (2;11,10,10), (2;11,10,11), (2;11,11,10), (2;11,11,11).
, на автомат подано неизвестное входное слово длиной 3, а по 1-му выходному каналу при этом наблюдалась реакция 0,1,1. Строим последовательность пар "состояние - входное слово", упомянутую в пункте 1 алгоритма: (1;10,00,10), (1;10,00,11), (1;10,00,00), (1;10,00,11), (1;10,01,10), (1;10,01,11), (1;10,01,00), (1;10,01,10), (1;11,00,10), (1;11,00,11), (1;11,00,00), (1;11,00,10), (1;11,01,10), (1;11,01,11), (1;11,01,00), (1;11,01,10), (2;10,10,10), (2;10,10,11), (2;10,11,10), (2;10,11,11), (2;11,10,10), (2;11,10,11), (2;11,11,10), (2;11,11,11).

