Обобщенные автоматы без потери информации конечного порядка
Автоматы без потери информации конечного порядка (ОБПИК-автоматы) являются в некотором смысле аналогами БПИК-автоматов, введенных С. Ивеном [74].
В этом разделе нами используется в качестве математической модели дискретного устройства слабоинициальный автомат Мили со структурированными входными и выходными алфавитами. Условимся также применять далее те же обозначения, понятия и конструкции, что были введены в предшествующем разделе.
Для однозначности определения числа 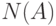 будем считать, что оно является минимальным из всех возможных для заданного автомата
будем считать, что оно является минимальным из всех возможных для заданного автомата  чисел такого рода, и назовем его порядком автомата
чисел такого рода, и назовем его порядком автомата  .
.
Отметим, что определенные нами ОБПИК-автоматы в качестве частного случая включают в себя ранее известные БПИК-автоматы, введенные  . Ивеном [74] , и автоматы существенно без потери информации конечного порядка (СБПИК-автоматы), введенные автором представленного курса лекций в [9], [46]. БПИК-автоматы получаются при
. Ивеном [74] , и автоматы существенно без потери информации конечного порядка (СБПИК-автоматы), введенные автором представленного курса лекций в [9], [46]. БПИК-автоматы получаются при 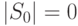 ,
, 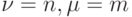 , а СБПИК-автоматы получаются при
, а СБПИК-автоматы получаются при  , где
, где  - число входных каналов автомата.
- число входных каналов автомата.
Пусть 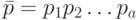 и
и 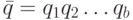 - слова в структурированном алфавите
- слова в структурированном алфавите  . Из определения ОБПИК-автомата порядка
. Из определения ОБПИК-автомата порядка 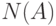 следует, что он должен обладать следующим свойством:
следует, что он должен обладать следующим свойством:
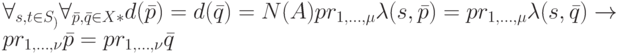 |
( 4.1) |
Здесь, не теряя общности, предполагается, что наблюдение реакции ведется по первым  выходным каналам с номерами
выходным каналам с номерами  , а неизвестное слово будет восстанавливаться по первым
, а неизвестное слово будет восстанавливаться по первым  входным каналам с номерами
входным каналам с номерами 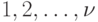 .
.
Теорема 4.1. Автомат  является ОБПИК-автоматом тогда и только тогда, когда в его проверочном графе
является ОБПИК-автоматом тогда и только тогда, когда в его проверочном графе  все контуры и все пути, ведущие в эти контуры, не содержат выделенных дуг.
все контуры и все пути, ведущие в эти контуры, не содержат выделенных дуг.
Необходимость. Пусть  есть ОБПИК-автомат порядка
есть ОБПИК-автомат порядка 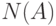 . Покажем, что он одновременно является и ОБПИ-автоматом. Пусть на вход
. Покажем, что он одновременно является и ОБПИ-автоматом. Пусть на вход  подано неизвестное входное слово
подано неизвестное входное слово  , такое, что
, такое, что 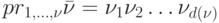 , а реакция
, а реакция  автомата
автомата  на это слово такова, что
на это слово такова, что 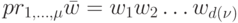 . Подадим на вход
. Подадим на вход  произвольное слово
произвольное слово 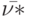 длины
длины 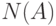 (пусть
(пусть 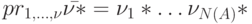 ), реакция на которое есть слово
), реакция на которое есть слово  (пусть
(пусть 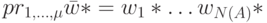 ). Поскольку
). Поскольку  есть ОБПИК-автомат порядка
есть ОБПИК-автомат порядка 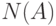 , то по начальному отрезку проекции выходного слова
, то по начальному отрезку проекции выходного слова 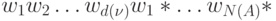 длины
длины 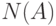 можно определить 1-й символ
можно определить 1-й символ 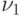 неизвестного входного слова, аналогично по начальному отрезку длины
неизвестного входного слова, аналогично по начальному отрезку длины 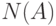 слова
слова 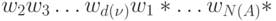 - символ
- символ 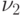 и, наконец, по начальному отрезку длины
и, наконец, по начальному отрезку длины 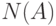 слова
слова 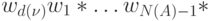 - символ
- символ 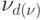 . Таким образом, подача на вход автомата
. Таким образом, подача на вход автомата  произвольного слова длины
произвольного слова длины 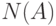 является тем экспериментом, который всегда позволяет определить искомую проекцию неизвестного входного слова. Следовательно,
является тем экспериментом, который всегда позволяет определить искомую проекцию неизвестного входного слова. Следовательно,  является ОБПИ-автоматом.
является ОБПИ-автоматом.
Предположим, что в  имеется контур
имеется контур 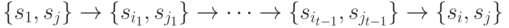 длины
длины  , первая дуга которого - выделенная. В силу теоремы 3.2 предшествующей лекции все вершины
, первая дуга которого - выделенная. В силу теоремы 3.2 предшествующей лекции все вершины 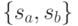 этого контура таковы, что
этого контура таковы, что 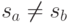 . Обозначим через
. Обозначим через 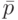 и
и 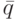 входные слова, соответствующие проходу автомата
входные слова, соответствующие проходу автомата  по состояниям контуров
по состояниям контуров  и
и  . Поскольку 1-я дуга контура в
. Поскольку 1-я дуга контура в  является выделенной, то
является выделенной, то 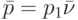 и
и 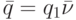 , где
, где 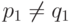 . Если к автомату
. Если к автомату  , находящемуся в состоянии
, находящемуся в состоянии 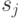 или
или 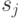 , приложить входные слова вида
, приложить входные слова вида  и
и 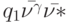 , где
, где  - целое положительное число,
- целое положительное число, 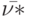 - некоторый начальный отрезок слова
- некоторый начальный отрезок слова  -кратное повторение слова
-кратное повторение слова  , то понятно, что наблюдаемые проекции автомата в обоих случаях будут одинаковыми. Следовательно, по наблюдаемой реакции восстановить однозначно 1-й символ неизвестного входного слова невозможно. Поскольку сказанное справедливо для любого
, то понятно, что наблюдаемые проекции автомата в обоих случаях будут одинаковыми. Следовательно, по наблюдаемой реакции восстановить однозначно 1-й символ неизвестного входного слова невозможно. Поскольку сказанное справедливо для любого  и начального отрезка
и начального отрезка 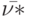 любой длины, то упомянутая потеря информации будет иметь место для слов произвольной длины. Последний факт противоречит исходному предположению о том, что
любой длины, то упомянутая потеря информации будет иметь место для слов произвольной длины. Последний факт противоречит исходному предположению о том, что  является ОБПИК-автоматом.
является ОБПИК-автоматом.
Нетрудно убедиться, что аналогичная ситуация имеет место и в случае, когда в графе  существует путь, ведущий в контур и начинающийся с выделенной дуги.
существует путь, ведущий в контур и начинающийся с выделенной дуги.
На этом завершается доказательство необходимости условий теоремы.
Достаточность. Пусть  не содержит контуров и, следовательно, в нем имеются только пути конечной длины. Рассмотрим вначале случай, когда эти пути не содержат выделенных дуг. Покажем, что в этих предположениях однозначное восстановление проекции первого символа неизвестного входного слова длины
не содержит контуров и, следовательно, в нем имеются только пути конечной длины. Рассмотрим вначале случай, когда эти пути не содержат выделенных дуг. Покажем, что в этих предположениях однозначное восстановление проекции первого символа неизвестного входного слова длины 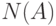 возможно. Предположим противное: пусть в
возможно. Предположим противное: пусть в  существует два пути
существует два пути

и
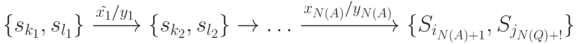
где  . Очевидно, что если проекция реакции автомата
. Очевидно, что если проекция реакции автомата  есть
есть  , то проекцию 1-го искомого символа восстановить однозначно невозможно. Однако в этом случае в
, то проекцию 1-го искомого символа восстановить однозначно невозможно. Однако в этом случае в  должны существовать выделенные дуги
должны существовать выделенные дуги 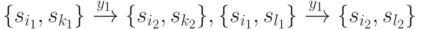 и т. д., что противоречит исходному предположению.
и т. д., что противоречит исходному предположению.
Теперь рассмотрим случай, когда в графе  содержится путь
содержится путь 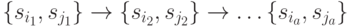 , у которого 1-я дуга является выделенной. Отсутствие в вершине
, у которого 1-я дуга является выделенной. Отсутствие в вершине 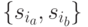 исходящей дуги означает, что при любом входном сигнале реакции автомата
исходящей дуги означает, что при любом входном сигнале реакции автомата  из состояний
из состояний 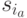 и
и 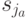 различны. Но тогда по этой реакции идентифицируется истинное состояние автомата (
различны. Но тогда по этой реакции идентифицируется истинное состояние автомата ( 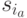 или
или 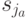 ). Поскольку по теореме 3.2 предшествующей лекции для вершины
). Поскольку по теореме 3.2 предшествующей лекции для вершины 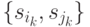 упомянутого выше пути
упомянутого выше пути 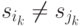 при
при 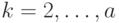 , то обратным ходом можно идентифицировать истинную последовательность сменяющихся состояний автомата
, то обратным ходом можно идентифицировать истинную последовательность сменяющихся состояний автомата  из двух возможных:
из двух возможных: 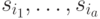 либо
либо 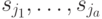 . Отсюда вытекает, что проекция первого символа неизвестного входного слова восстанавливается однозначно.
. Отсюда вытекает, что проекция первого символа неизвестного входного слова восстанавливается однозначно.
Перейдем к рассмотрению случая, когда в графе  имеются контуры. Доказательство для него проведем от противного. Пусть
имеются контуры. Доказательство для него проведем от противного. Пусть  не является ОБПИК-автоматом. В частности, в нем могут существовать два контура:
не является ОБПИК-автоматом. В частности, в нем могут существовать два контура:

и
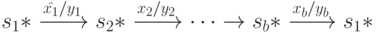
где происходит потеря информации о первом входном символе, если  . Но тогда в графе
. Но тогда в графе  существует контур
существует контур 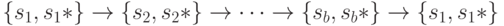 , у которого 1-я дуга является выделенной. Отсюда вытекает справедливость достаточности условий теоремы для контуров с выделенными дугами. По аналогии устанавливается справедливость условий теоремы и для случая путей с выделенными дугами, ведущими в контур. На этом завершается доказательство достаточности условий теоремы.
, у которого 1-я дуга является выделенной. Отсюда вытекает справедливость достаточности условий теоремы для контуров с выделенными дугами. По аналогии устанавливается справедливость условий теоремы и для случая путей с выделенными дугами, ведущими в контур. На этом завершается доказательство достаточности условий теоремы.
Следующее утверждение позволяет определить порядок ОБПИК-автомата .
Теорема 4.2. Если в проверочном графе  ОБПИК-автомата
ОБПИК-автомата  длина максимального пути, начальная дуга которого является выделенной, равна
длина максимального пути, начальная дуга которого является выделенной, равна  , то порядок ОБПИК-автомата
, то порядок ОБПИК-автомата  .
.
Доказательство. Пусть в  существует путь, начинающийся в вершине
существует путь, начинающийся в вершине  и заканчивающийся в
и заканчивающийся в  , 1-я дуга которого является выделенной. Наличие его означает существование у автомата
, 1-я дуга которого является выделенной. Наличие его означает существование у автомата  двух входных слов
двух входных слов  и
и 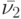 , различающихся проекциями первых символов и обладающих следующим свойством:
, различающихся проекциями первых символов и обладающих следующим свойством:
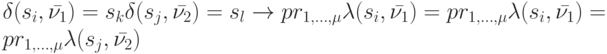
При распознавании проекции неизвестного входного слова автомата  мы не располагаем информацией об истинном его начальном состоянии. Если на вход автомата
мы не располагаем информацией об истинном его начальном состоянии. Если на вход автомата  будет подано одно из слов
будет подано одно из слов  или
или 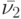 , то мы не сможем определить и его истинное конечное состояние. В этой ситуации определение проекции 1-го символа входного слова по наблюдаемой реакции длины не более
, то мы не сможем определить и его истинное конечное состояние. В этой ситуации определение проекции 1-го символа входного слова по наблюдаемой реакции длины не более  символов невозможно. Это означает, что порядок автомата
символов невозможно. Это означает, что порядок автомата  заведомо больше
заведомо больше  . Поскольку путь рассматриваемого вида максимален по длине, то из вершины
. Поскольку путь рассматриваемого вида максимален по длине, то из вершины 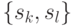 графа
графа  не может исходить ни одной дуги. Для автомата
не может исходить ни одной дуги. Для автомата  этот факт интерпретируется следующим образом: если автомат
этот факт интерпретируется следующим образом: если автомат  находится в одном из состояний
находится в одном из состояний 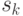 или
или 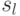 , то подача любого входного символа и наблюдение соответствующей реакции автомата позволяет всегда однозначно определить истинное начальное состояние из двух допустимых. Отсюда можно сделать вывод, что знание проекции реакции автомата на неизвестное входное слово длины
, то подача любого входного символа и наблюдение соответствующей реакции автомата позволяет всегда однозначно определить истинное начальное состояние из двух допустимых. Отсюда можно сделать вывод, что знание проекции реакции автомата на неизвестное входное слово длины  всегда позволяет однозначно определить проекцию 1-го символа этого входного символа.
всегда позволяет однозначно определить проекцию 1-го символа этого входного символа.
Докажем это утверждение от противного. Пусть существуют два различных входных слова  и
и 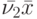 , где
, где  и
и 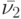 - слова, упомянутые ранее, а
- слова, упомянутые ранее, а 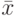 - произвольный символ из
- произвольный символ из  . Пре
дположим, что автомат находится в состоянии
. Пре
дположим, что автомат находится в состоянии  или
или 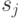 . Если на вход автомата
. Если на вход автомата  будет подано одно из слов
будет подано одно из слов  или
или 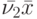 , то по проекции последнего выходного символа можно определить состояние, в котором автомат находился перед подачей символа
, то по проекции последнего выходного символа можно определить состояние, в котором автомат находился перед подачей символа 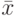 . Неоднозначность определения проекции 1-го символа неизвестного входного слова в нашей ситуации означало бы, что
. Неоднозначность определения проекции 1-го символа неизвестного входного слова в нашей ситуации означало бы, что 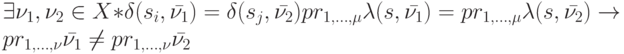 .
.
Тогда в соответствии с определением 3.1 состояния  и
и 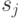 образуют пару СПИ-состояний. Отсюда следует, что автомат
образуют пару СПИ-состояний. Отсюда следует, что автомат  не может принадлежать классу ОБПИ-автоматов, а в силу теоремы 4.1 он не может принадлежать и классу СБПИК-автоматов. Последний факт противоречит нашему предположению.
не может принадлежать классу ОБПИ-автоматов, а в силу теоремы 4.1 он не может принадлежать и классу СБПИК-автоматов. Последний факт противоречит нашему предположению.
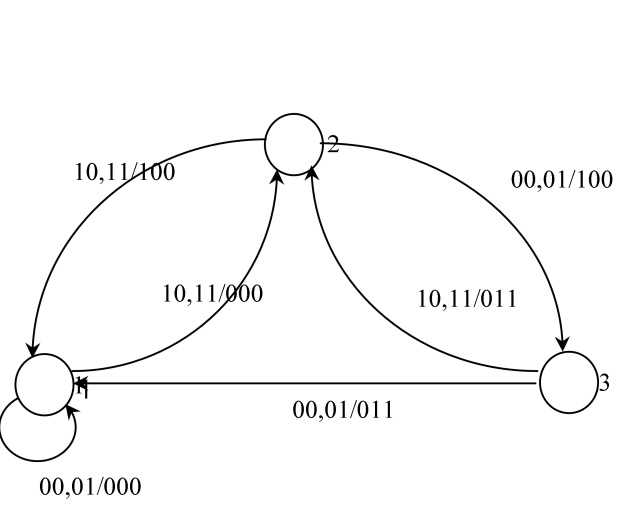
Рассмотрим автомат, заданный графом на рис.4.1. Пусть его реакция наблюдается по 1-му и 2-му выходным каналам ( 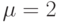 ), а проекция неизвестного входного слова должна восстанавливаться по 1-му каналу (
), а проекция неизвестного входного слова должна восстанавливаться по 1-му каналу ( 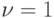 ). Пусть
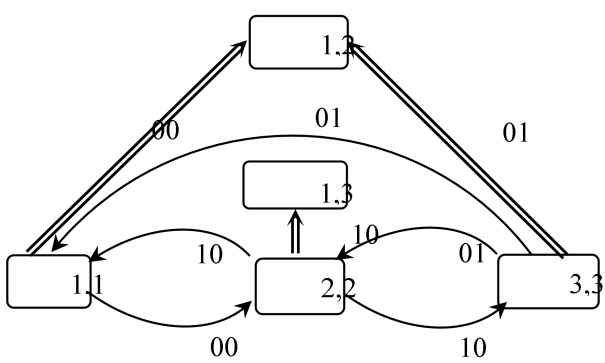
). Пусть 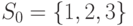 , тогда проверочный граф для этого автомата изображен на рис.4.2. Легко проверить, что условия теоремы 4.1 для графа на рис.4.2 выполняются, следовательно, рассматриваемый автомат есть ОБПИК. Поскольку длины всех путей в графе
, тогда проверочный граф для этого автомата изображен на рис.4.2. Легко проверить, что условия теоремы 4.1 для графа на рис.4.2 выполняются, следовательно, рассматриваемый автомат есть ОБПИК. Поскольку длины всех путей в графе  , начальные дуги которых являются выделенными, равны
, начальные дуги которых являются выделенными, равны  , то порядок автомата
, то порядок автомата  .
.
В табл. 4.1 приведены все возможные реакции автомата на входные слова длины 2 и соответствующие им проекции 1-го символа неизвестного входного слова по 1-му входному каналу.
| Реакция автомата по каналам 1 и 2 | Проекция 1-го входного символа по каналу 1 |
|---|---|
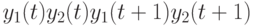 |
|
|
0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 0 1 |
0 1 0 1 1 0 |
Рассмотрим вопрос о восстановлении проекции 1-го символа неизвестного входного слова. Из (4.1) следует, что каждой комбинации из 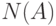 символов, являющихся проекциями реакций автомата
символов, являющихся проекциями реакций автомата  по выходным каналам с номерами
по выходным каналам с номерами 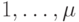 , однозначно соответствует искомая проекция 1-го символа неизвестного входного слова. В частности, такое соответствие для автомата на рис.4.1 задано табл. 4.1. Подобную таблицу будем интерпретировать далее как совокупность
, однозначно соответствует искомая проекция 1-го символа неизвестного входного слова. В частности, такое соответствие для автомата на рис.4.1 задано табл. 4.1. Подобную таблицу будем интерпретировать далее как совокупность  таблиц истинности частичных булевых функций, где
таблиц истинности частичных булевых функций, где  - число каналов, по которым производится восстановление неизвестного входного слова. Строки первого столбца таблицы типа табл. 4.1 содержат двоичные наборы длины
- число каналов, по которым производится восстановление неизвестного входного слова. Строки первого столбца таблицы типа табл. 4.1 содержат двоичные наборы длины 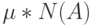 , на которых упомянутые булевы функции считаются заданными, а значение на соответствующем наборе
, на которых упомянутые булевы функции считаются заданными, а значение на соответствующем наборе  -й булевой функции полагается равным величине, стоящей в
-й булевой функции полагается равным величине, стоящей в  -й позиции второго столбца таблицы, где
-й позиции второго столбца таблицы, где 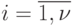 .
.
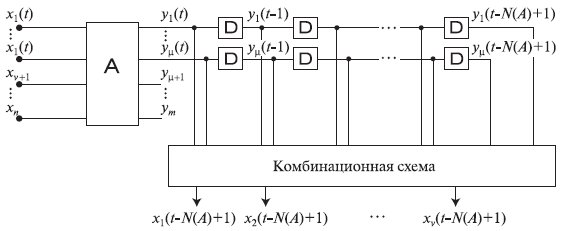
Исходя из предложенной интерпретации, общая схема восстановления некоторой проекции неизвестного входного слова для ОБПИК-автомата порядка 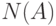 с использованием комбинационного устройства, реализующего совокупность
с использованием комбинационного устройства, реализующего совокупность  частичных булевых функций, изображена на рис.4.3. На этом рисунке
частичных булевых функций, изображена на рис.4.3. На этом рисунке  означает элемент единой задержки. На рис.4.4 изображена схема восстановления, которая построена на основе табл. 4.1 для автомата, представленного на рис.4.1.
означает элемент единой задержки. На рис.4.4 изображена схема восстановления, которая построена на основе табл. 4.1 для автомата, представленного на рис.4.1.
По аналогии с оптимальными ОБПИ-автоматами, введенными в предыдущей лекции, рассмотрим ОБПИК-автоматы. Для их отыскания по графу автомата  построим проверочный граф
построим проверочный граф  , предполагая, что наблюдение реакции ведется по всем
, предполагая, что наблюдение реакции ведется по всем  выходным, а восстановление - по всем
выходным, а восстановление - по всем  входным каналам. Используя
входным каналам. Используя  , найдем в нем все контуры и все пути, ведущие в эти контуры, образуем на этой основе множество
, найдем в нем все контуры и все пути, ведущие в эти контуры, образуем на этой основе множество 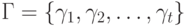 всех входящих в них выделенных дуг. Если
всех входящих в них выделенных дуг. Если  , то по теореме 4.1 автомат
, то по теореме 4.1 автомат  есть ОБПИК и при
есть ОБПИК и при 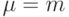 он будет таковым для любого
он будет таковым для любого 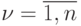 . Если
. Если  , то для каждого
, то для каждого 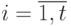 построим множество
построим множество 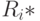 целых чисел, являющихся номерами входных каналов, в которых на дуге
целых чисел, являющихся номерами входных каналов, в которых на дуге  происходит потеря информации в смысле, определенном в предыдущем разделе. По аналогии с ОБПИ-автоматами можно утверждать, что
происходит потеря информации в смысле, определенном в предыдущем разделе. По аналогии с ОБПИ-автоматами можно утверждать, что  является ОБПИК для любого подмножества каналов из множества
является ОБПИК для любого подмножества каналов из множества 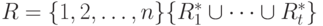 и
и  есть максимальное по мощности множество каналов, сохраняющее свойство ОБПИК.
есть максимальное по мощности множество каналов, сохраняющее свойство ОБПИК.
Пусть 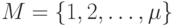 . Для
. Для 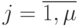 строим проверочный граф
строим проверочный граф 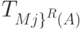 . Если он удовлетворяет условиям теоремы 4.1, то
. Если он удовлетворяет условиям теоремы 4.1, то  -й канал является избыточным в смысле, определенном в предыдущей лекции. Пусть
-й канал является избыточным в смысле, определенном в предыдущей лекции. Пусть 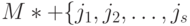 - множество номеров всех избыточных выходных каналов автомата
- множество номеров всех избыточных выходных каналов автомата  . Если
. Если 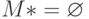 , то
, то 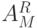 является искомым оптимальным автоматом. При
является искомым оптимальным автоматом. При  рассмотрим всевозможные сочетания пар, троек и т. д. номеров каналов из
рассмотрим всевозможные сочетания пар, троек и т. д. номеров каналов из 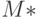 . Обозначим
. Обозначим 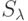 множество, содержащее
множество, содержащее  номеров из
номеров из 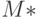 , где
, где 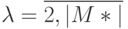 . Для каждого из множеств
. Для каждого из множеств 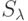 начиная с
начиная с 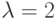 строим проверочный граф
строим проверочный граф  . Если для всевозможных множеств
. Если для всевозможных множеств 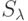 при
при 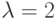 соответствующие им проверочные графы удовлетворяют условиям теоремы 4.1, то увеличиваем
соответствующие им проверочные графы удовлетворяют условиям теоремы 4.1, то увеличиваем  на 1 и продолжаем этот процесс. Если на очередном этапе каждый из построенных для всевозможных множеств
на 1 и продолжаем этот процесс. Если на очередном этапе каждый из построенных для всевозможных множеств 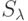 проверочных графов не удовлетворяет условиям теоремы 4.1, то процесс прекращается. При этом очевидно, что оптимальными будут все те автоматы
проверочных графов не удовлетворяет условиям теоремы 4.1, то процесс прекращается. При этом очевидно, что оптимальными будут все те автоматы 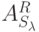 , рассмотренные на предпоследнем этапе (для них
, рассмотренные на предпоследнем этапе (для них  имеет значение на 1 меньше, чем на последнем этапе), для которых соответствующие графы удовлетворяют условиям теоремы 4.1.
имеет значение на 1 меньше, чем на последнем этапе), для которых соответствующие графы удовлетворяют условиям теоремы 4.1.
Вопросы и упражнения
- Сформулируйте определение обобщенного автомата без потери информации конечного порядка.
- Приведите критерий принадлежности автомата классу автоматов ОБПИК в терминах проверочного графа.
- Опишите процедуру определения порядка ОБПИК-автомата.
- Опишите процедуру построения комбинационной схемы, позволяющей восстанавливать проекцию неизвестного входного слова ОБПИК-автомата.
- Автомат задан графом на рис.4.1. Пусть множество допустимых начальных состояний автомата есть
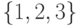 . Пусть для наблюдения реакции доступны оба выходных канала, а проекция неизвестного входного слова должна быть восстановлена по 2-му каналу. Требуется:
. Пусть для наблюдения реакции доступны оба выходных канала, а проекция неизвестного входного слова должна быть восстановлена по 2-му каналу. Требуется: