НОУ ИНТУИТ | Теория экспериментов с конечными автоматами. Лекция 12: Эксперименты в пространстве обобщенных состояний и с линейными автоматами с запаздыванием

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 17.02.2011 | Доступ: свободный | Студентов: 367 / 35 | Оценка: 5.00 / 5.00 | Длительность: 25:24:00

ISBN: 978-5-9963-0268-0

Тема: Алгоритмы и дискретные структуры

Специальности: Математик

|

Вам нравится? Нравится 3 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Эксперименты с линейными автоматами с запаздыванием

Выше были рассмотрены ЛА, в правых частях уравнений переходов и выходов которых фигурировали векторы и матрицы со значениями только в момент времени . Вместе с тем многие реальные процессы и устройства требуют для своего описания использования уравнений с запаздыванием.

Ниже будет использована классификация произвольных дискретных систем (ДС) с запаздыванием, предложенная в [17]. Очевидно, что эта классификация годится и для рассматриваемого нами частного случая ДС - линейных автоматов, заданных над полем 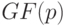GF(p) . В приведенных ранее обозначениях упомянутая классификация ДС такова:

Обыкновенная ДС - поведение ее описывается уравнением

$\bar s(t+ \alpha )+A_1\bar s(t+ \alpha -1)+ \dots + A_{\alpha}\bar s(t)=B_0\bar u(t+ \beta)+ \dots +B_{\beta}\bar u(t), \beta < \alpha$

( 12.8)

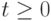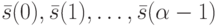Для того чтобы движение обыкновенной ДС было однозначно определено при $t \ge 0$ , для любого входа $\bar u(t)$ должны быть заданы начальные условия $\bar s(0), \bar s(1), \dots, \bar s(\alpha -1)$ и $\bar u(0), \bar u(1), \dots, \bar u(\beta - 1)$

ДС с запаздыванием по состоянию - поведение ее описывается уравнением

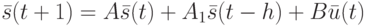$\bar s(t+1)=A\bar s(t)+A_1\bar s(t-h)+B\bar u(t)$

( 12.9)

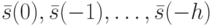Для однозначного определения процесса $\bar s(t)$ при любом входе $\bar u(t)$ задаются начальные условия $\bar s(0), \bar s(-1), \dots, \bar s(-h)$ , где - некоторое положительное целое число.

ДС с запаздыванием по управлению - поведение ее описывается уравнением

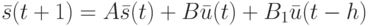$\bar s(t+1)=A\bar s(t)+B\bar u(t)+B_1\bar u(t-h)$

( 12.10)

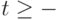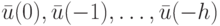Для однозначности определения процесса $\bar s(t)$ при $t \ge -$ при любом входе $\bar u(t)$ должны быть заданы начальные условия $\bar s(0)$ и $\bar u(0), \bar u(-1), \dots, \bar u(-h)$ , где - некоторое положительное целое число.

В этом разделе будут рассмотрены вопросы существования СП, УП и ДП и методы их построения для линейных автоматов с запаздыванием, уравнения переходов которых представлены формулами (12.8)-(12.10).

Для получения критериев существования различных типов экспериментов для ЛА с запаздыванием используем следующую идею, изложенную в[71]. Попытаемся из фазового пространства состояний исходной ДС с запаздыванием по состоянию перейти в новое фазовое пространство состояний большей размерности с тем, чтобы уравнение состояний при этом трансформировалось в уравнение состояний ЛА без запаздывания. Аналогичное преобразование проделаем и в случае ЛА с запаздыванием по управлению, переходя от исходного входного вектора к вектору большей размерности с целью получения уравнений ЛА без запаздывания.

Из приведенных выше описаний ДС можно заключить, что участвующие в них векторы $\bar s(t)$ , вообще говоря, не всегда представляют собой состояние системы в общепринятом смысле, т. е. ту минимальную по объему информацию, которую необходимо знать в текущий момент времени для однозначного продолжения процесса $\bar s(t)$ при известном входе $\bar u(t)$ Учитывая сказанное, каждую из перечисленных выше ДС с запаздыванием мы опишем в виде ЛА, определив соответствующим образом для ДС различных типов уравнение ее состояний, а затем для формулировки условий существования СП для этой ДС воспользуемся соответствующим критерием, полученным для ЛА без запаздывания.

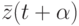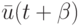Рассмотрим вначале обыкновенную ДС, заданную уравнением (12.8). Состояние $\bar z(t+\alpha)$ этой ДС в произвольный момент времени $t+\alpha$ определим как вектор $[\bar s(t), \bar s(t+1), \dots, \bar s(t + \alpha +1)]'$ Тогда состояние, в которое она переходит при подаче входного сигнала $\bar u(t+ \beta)$ , есть вектор $\bar u(t+\alpha +1)=[\bar s(t+1), \dots, \bar s(t+ \alpha)]'$ . 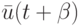Таким образом, если эту ДС описывать в виде ЛА, то размерность такого ЛА есть величина $n=m \alpha$ а начальное состояние есть $\bar z(0)=[\bar s(0), \bar s(1), \dots, \bar s(\alpha +1)]'$ В качестве входного вектора $\bar u(t+\beta)$ этой ДС теперь будем использовать вектор $\tilde u(t+\beta)=[\bar u(t), \bar u(t+1), \dots, \bar u(t+\beta)]'$ С учетом изложенного, если описывать рассматриваемую ДС в виде ЛА, уравнение ее переходов состояний примет вид

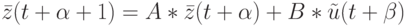$\bar z(t+ \alpha +1)=A*\bar z(t+ \alpha)+B* \tilde u(t+\beta)$

( 12.11)

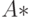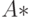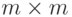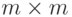Матрицы и имеют блочную структуру, которая описывается ниже. В роли блоков в матрице выступают матрицы размерности $m \times m$ , а число "блочных" строк и столбцов ее равно величине $\alpha$ Структура этой матрицы имеет следующий вид ( E_m - единичная матрица размером $m \times m$ ):

$A*= \left [ \begin {matrix} [0]&E_m&[0] &\dots & [0]\\ [0]&[0]&E_m& \dots &[0]\\ \dots &a \dots & \dots & \dots &\dots \\ [0]&[0]&[0]& \dots E_m\\ \A_{\alpha}& -A_{\alpha -1}& -A_{\alpha -2}& \dots -A_1 \end {matrix} \right ]$

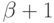В роли блоков матрицы выступают матрицы размерности $m \times l$ . Число "блочных" строк в равно $\alpha$ , а число "блочных" столбцов - $\beta +1$ . Структура этой матрицы такова:

$B*= \left [ \begin {matrix} [0]&[0]&[0]&\dots &[0]\\ [0]&[0]&[0]& \dots &[0]\\ \dots & \dots & \dots & \dots &\dots\\ [0] &[0]&[0]& \dots [0]\\ B_{\beta}&b_{\beta -1}&B_{\beta -2}& \dots &B_0 \end {matrix} \right ]$

Непосредственной проверкой можно убедиться, что уравнение (12.11) с такими характеристическими матрицами задает линейный автомат, эквивалентный, с точки зрения функционирования, обыкновенной ДС, описанной разностным уравнением (1.1), откуда следует справедливость следующего утверждения:

Теорема 1.1 Для того чтобы ЛА с запаздыванием, описанный уравнением (12.8), имел СП длины , необходимо и достаточно, чтобы выполнялось условие (A*)^k .

Рассмотрим теперь ДС с запаздыванием по состоянию. Состояние ее в произвольный момент времени определим как вектор $\bar z(t)=[\bar s(t-h), \bar s(t-h+1), \dots, \bar s(t)]'$ Тогда следующее состояние после подачи очередного входа будет $\bar z(t+1)=[\bar s(t)(h+1), \dots, \bar s(t), \bar s(t+1)]'$ Следовательно, при описании этой ДС в виде ЛА размерность последнего равна величине n=m(h+1) , а начальное состояние есть $\bar z(0)=[\bar s(0), \bar s(-1), \dots, \bar s(-h)]$ , компонентами которого являются заданные начальные условия. Учитывая сказанное, при описании ДС с запаздыванием по состоянию в виде ЛА уравнение переходов состояний примет вид

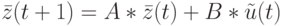
$\bar z(t+1)=A*\bar z(t)+B* \tilde u(t)$

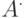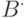где матрицы $A^{\cdot}$ и $B^{\cdot}$ так же, как и в предыдущем случае, имеют блочную структуру. В роли блоков в матрице 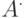$A^{\cdot}$ выступают матрицы размерности 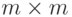$m \times m$ , а число ее "блочных" строк и столбцов равно h+1 :

$A*= \left [ \begin {matrix} [0]&E_m&[0]& \dots &[0]\\ [0]&[0]&E_m& \dots &[0]\\ \dots &\dots &\dots &\dots &\dots\\ [0]&[0]&[0]& \dots &E_m\\ A_1&[0]&[0]& \dots &A \end {matrix} \right ]$

В роли блоков в матрице выступают матрицы размерности $m \times l$ , "блочных" строк в ней одна, а число столбцов - h+1 :

$B*=[[0] \dots [0]B]'$

Можно проверить, что уравнение (10.1) с приведенными характеристическими матрицами задают ЛА, эквивалентный, с точки зрения функционирования, ДС с запаздыванием по состоянию, описанную уравнением (12.9). Отсюда следует, что для ДС такого типа справедлив аналог теоремы 10.1.

Рассмотрим, наконец, ДС с запаздыванием по управлению. При описании в виде ЛА состояние последнего в момент времени отождествим с вектором $\bar s(t)$ из (12.10), а входным вектором ЛА теперь будет являться вектор

$\tilde u(t)=[\bar u(t), \bar u(t-1), \dots, \bar u(t-h)]'$

Тогда очевидно, что основная характеристическая матрица соответствующего ЛА просто совпадает с матрицей из (1.1), а в роли матрицы в формуле (1.1) будет выступать "блочный" вектор

$B*=[B[0] \dots [0] B_1]'$

Из изложенного следует, что условие существования СП для ДС с запаздыванием по управлению просто совпадает с соответствующим условием для ЛА, описанного уравнением (1.1).

Подводя итог, отметим, что каждой из перечисленных выше типов ДС можно поставить в соответствие такой ЛА без запаздывания, который эквивалентен соответствующей ДС по поведению. Отсюда следует, что ранее доказанные для ЛА без запаздывания утверждения оказываются справедливыми для ЛА с запаздыванием. В частности, для них имеют место аналоги теорем 1.2, 1.3, следствие из теоремы 1.1 и т. д.

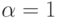Кроме того, для решения задачи о переводе ЛА с запаздыванием в заданное синхросостояние остается пригодным метод, описанный в разделе 1.2 лекции 1. Проиллюстрируем это на примере применительно к обыкновенной ДС над полем GF(2) при $\alpha = 1$ и $\beta =1$ , заданной уравнением

$\bar s (t+2)+A_1 \bar s(t+1)+A_2 \bar s(t)=B_0\bar u(t+1)+B_1 \bar u(t)$

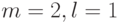где $\bar s(t)=[s_1(t), s_2(t)]'$ и $\bar u(t)=[u_1(t)]'$ , т. е. m=2, l=1 , а характеристические матрицы ДС имеют следующий вид:

$A_1= \left [ \begin {matrix} 0&1\\ 0&0 \end {matrix} \right ], A_2= \left [ \begin {matrix} 0&0\\ 0&0 \end {matrix} \right ], B_0= \left [ \begin {matrix} 0\\ 1 \end {matrix} \right ], B_1= \left [ \begin {matrix} 1\\ 0 \end {matrix} \right ]$

Вычисления показывают, что эквивалентный рассматриваемой системе ЛА имеет следующие характеристические матрицы:

$A*= \left [ \begin {matrix} 0&0&1&0\\ 0&0&0&1\\ 0&0&0&1\\ 0&0&0&0 \end {matrix} \right ], B*= \left [ \begin {matrix} 0&0\\ 0&0\\ 1&0\\ 0&1 \end {matrix} \right ]$

При этом состоянием ЛА и его входным вектором являются векторы:

$\bar s(t)=[s_1(t), s_2(t), s_1(t+1), s_2(t+1]', \dots, \bar u(t)=[u_1(t), u_1(t+1)]'$

Пусть задано синхросостояние $\tilde s=[0,1,0,1]'$ и требуется найти такую входную последовательность, которая переводит ДС из произвольного начального состояния в синхросостояние $\tilde s$ .

Легко проверить, что (A*)^3=[0] откуда вытекает, что эквивалентный рассматриваемой системе ЛА синхронизируем и длина минимальной СП равна 3. Для нахождения искомой СП выпишем матричное уравнение вида (1.14) для нашего примера:

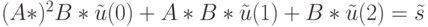
$(A*)^2B* \tilde u(0)+A*B* \tilde u(1)+B*\tilde u(2)= \tilde s$

С учетом приведенных выше матриц 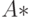и это уравнение принимает следующий вид:

$\left [ \begin {matrix} 0&1\\ 0&0\\ 0&0\\ 0&0 \end {matrix} \right ] \times \left [ \begin {matrix} u_1(0)\\ u_1(1) \end {matrix} \right ] + \left [ \begin {matrix} 1&0\\ 0&1\\ 1&0\\ 0&0 \end {matrix} \right ] \times \left [ \begin {matrix} u_1(1)\\ u_2(1) \end {matrix} \right ] + \left [ \begin {matrix} 0&0\\ 0&0\\ 1&0\\ 0&1 \end {matrix} \right ] \times \left [ \begin {matrix} u_1(2)\\ u_1(3) \end {matrix} \right ] = \left [ \begin {matrix} 0\\ 1\\ -\\ 1 \end {matrix} \right ]$

Перейдем от этого уравнения к равносильной системе, записанной в координатной форме:

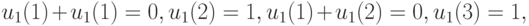
u_1(1)+ u_1(1)=0, u_1(2)=1, u_1(1)+ u_1(2)=0, u_1(3)=1,

где "+" - операция по модулю 2.

Легко проверить, что эта система совместна и ее решение таково:

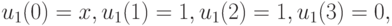
где х означает безразличное значение (0 или 1). Следовательно, для рассматриваемой ДС в качестве СП, переводящей ее из произвольного начального состояния в заданное синхросостояние $\tilde s$ , могут быть использованы две следующие входных последовательностей:

,
.

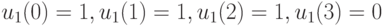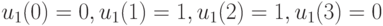Коснемся теперь критериев существования УП и ДП для ДС с запаздыванием.

Поскольку, как показано выше, каждый из рассматриваемых типов ДС соответствует эквивалентной ей ЛА без запаздывания, то критерий существования УП и ДП для ДС с запаздыванием - это теорема 1.4 и 2.1, в которых вместо матриц А и С должны фигурировать матрицы 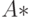и 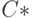эквивалентных ЛА. Кроме того, для ДС с запаздыванием оказываются справедливыми аналоги теорем 10.5, 11.1 и 11.3.

Вопросы и упражнения

Дайте определение обобщенного состояния автомата.
Укажите различие между классической диаграммой автомата и диаграммой автомата в пространстве обобщенных состояний.
Сформулируйте критерий управляемости обобщенного автомата в матричной форме.
Может ли автомат, не являющийся сильно связным в классическом понимании, оказаться сильно связным в пространстве обобщенных состояний?
Дайте определения обобщенных синхронизирующих, установочных и диагностических последовательностей.
Сформулируйте критерии существования таких последовательностей.
Являются ли свойства обобщенных последовательностей аналогами соответствующих свойств обычных последовательностей тех же типов для "классических" линейных автоматов?
Приведите классификацию линейных автоматов с запаздыванием. 9. Изложите основополагающую идею для получения критериев существования всех типов последовательностей для всех типов автоматов с запаздыванием.

Дальше >>

Авторизоваться

Теория экспериментов с конечными автоматами

Эксперименты в пространстве обобщенных состояний и с линейными автоматами с запаздыванием

Эксперименты с линейными автоматами с запаздыванием

Вопросы и упражнения

Вопросы и ответы