Контроль функции выходов инициального автомата с использованием кратного безусловного эксперимента
Определение 8.4. Приведенное покрытие графа, являющееся минимальным по кратности и по длине, назовем минимальным.
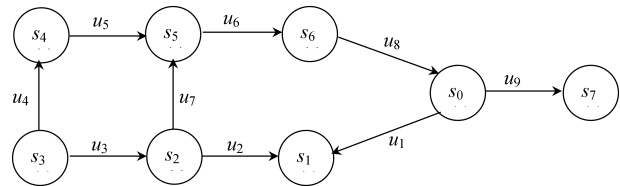
Покажем, что минимальное покрытие графа не всегда существует. С этой целью рассмотрим граф, изображенный на рис.8.2.
Покрытия  и
и  , как легко видеть, являются приведенными покрытиями этого графа. Покрытие
, как легко видеть, являются приведенными покрытиями этого графа. Покрытие 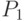 является минимальным по кратности (кратность его равна 1), но не минимальным по длине (длина его равна 13). Покрытие
является минимальным по кратности (кратность его равна 1), но не минимальным по длине (длина его равна 13). Покрытие 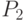 (длины 11 и кратности 2) является минимальным по длине, но не минимальным по кратности. Легко установить, что для данного графа минимального покрытия не существует.
(длины 11 и кратности 2) является минимальным по длине, но не минимальным по кратности. Легко установить, что для данного графа минимального покрытия не существует.
Перейдем к отысканию условий, при которых минимальное покрытие существует. Покажем справедливость следующего вспомогательного утверждения.
Лемма 8.5. Если  есть покрытие графа
есть покрытие графа  минимальной длины, то любой путь из
минимальной длины, то любой путь из  , не оканчивающийся в начальной вершине графа, оканчивается в некоторой положительной его вершине.
, не оканчивающийся в начальной вершине графа, оканчивается в некоторой положительной его вершине.
Доказательство. Пусть  - покрытие графа
- покрытие графа 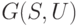 минимальной длины
минимальной длины  . Предположим, что существует путь
. Предположим, что существует путь 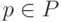 , оканчивающийся в некоторой не положительной вершине
, оканчивающийся в некоторой не положительной вершине  , где
, где 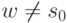 . Покрытию
. Покрытию  соответствует регулярный сильно связный сверхграф
соответствует регулярный сильно связный сверхграф  , способ построения которого описан при доказательстве леммы 8.3.
, способ построения которого описан при доказательстве леммы 8.3.
Преобразуем граф  следующим образом: каждую дугу
следующим образом: каждую дугу  заменим
заменим  дугами
дугами 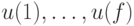 с тем же началом и концом, где
с тем же началом и концом, где  - число путей из
- число путей из  , содержащих дугу
, содержащих дугу  . Легко видеть, что полученный в результате граф
. Легко видеть, что полученный в результате граф 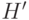 обладает эйлеровым контуром. Поскольку
обладает эйлеровым контуром. Поскольку  не обладает положительной вершиной графа
не обладает положительной вершиной графа  и
и 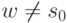 , то в графе
, то в графе  эта вершина отрицательна, а в графе
эта вершина отрицательна, а в графе 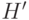 , очевидно,
, очевидно, 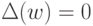 . Отсюда следует, что найдется такая дуга
. Отсюда следует, что найдется такая дуга 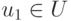 , оканчивающаяся в вершине
, оканчивающаяся в вершине  , что в графе
, что в графе 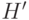 существуют дуги
существуют дуги 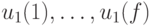 , где
, где  . Выполним следующее преобразование графа
. Выполним следующее преобразование графа 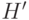 : исключим из него дугу
: исключим из него дугу 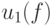 и одну замыкающую дугу, исходящую из
и одну замыкающую дугу, исходящую из  . Далее, из начальной вершины дуги
. Далее, из начальной вершины дуги 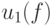 , если она отлична от
, если она отлична от  , проводим одну замыкающую дугу в
, проводим одну замыкающую дугу в  . Полученный в результате такого преобразования новый граф
. Полученный в результате такого преобразования новый граф 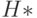 , как это следует из его построения, обладает эйлеровым контуром.
, как это следует из его построения, обладает эйлеровым контуром.
Число дуг графа 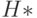 по крайней мере на единицу меньше числа дуг графа
по крайней мере на единицу меньше числа дуг графа 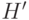 . Любому эйлерову контуру графа
. Любому эйлерову контуру графа 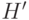 соответствует покрытие
соответствует покрытие 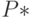 графа
графа  длины, не большей
длины, не большей  . Отсюда следует, что
. Отсюда следует, что  не является покрытием минимальной длины. Полученное противоречие доказывает лемму.
не является покрытием минимальной длины. Полученное противоречие доказывает лемму.
Сформулируем достаточное условие существования у графа минимального покрытия.
Теорема 8.4. Если у правильного графа множества 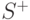 и
и 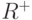 совпадают, то у него существует мимнимальное покрытие.
совпадают, то у него существует мимнимальное покрытие.
Доказательство. Если у правильного графа  множество
множество 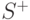 пусто, то он обладает эйлеровым контуром. Очевидно, что эйлеров контур является минимальным покрытием графа.
пусто, то он обладает эйлеровым контуром. Очевидно, что эйлеров контур является минимальным покрытием графа.
Предположим теперь, что множество 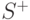 не пусто, следовательно,
не пусто, следовательно, 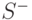 также не пусто. Поскольку
также не пусто. Поскольку  , а множество
, а множество 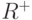 состоит из вершин, из которых не достижима ни одна отрицательная вершина, то граф
состоит из вершин, из которых не достижима ни одна отрицательная вершина, то граф  заведомо не является сильно связным. В силу следствия 1 теоремы 8.3 минимальная кратность покрытия графа
заведомо не является сильно связным. В силу следствия 1 теоремы 8.3 минимальная кратность покрытия графа  в таком случае равна (8.2).
в таком случае равна (8.2).
Пусть  есть покрытие графа
есть покрытие графа  минимальной длины
минимальной длины 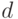 и каждый путь из
и каждый путь из  оканчивается в вершине, не равной
оканчивается в вершине, не равной  . Тогда по лемме 8.5 каждый путь из
. Тогда по лемме 8.5 каждый путь из  оканчивается в вершине множества
оканчивается в вершине множества 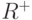 . Предположим, что
. Предположим, что  не минимально по кратности, т. е. его кратность
не минимально по кратности, т. е. его кратность  больше (8.1). Пусть покрытию
больше (8.1). Пусть покрытию  соответствует сильно связный регулярный граф
соответствует сильно связный регулярный граф  (см. доказательство леммы 8.2). По графу
(см. доказательство леммы 8.2). По графу  построим эйлеров граф
построим эйлеров граф 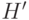 , заменяя каждую дугу
, заменяя каждую дугу  столькими дугами (с тем же началом и концом), скольким путям из
столькими дугами (с тем же началом и концом), скольким путям из  принадлежит дуга
принадлежит дуга  . Поскольку
. Поскольку  больше (8.1), то найдется вершина
больше (8.1), то найдется вершина 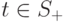 , из которой в графе
, из которой в графе  выходит
выходит  замыкающих дуг, где
замыкающих дуг, где 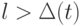 . Следовательно, в графе
. Следовательно, в графе  найдется дуга
найдется дуга 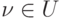 , входящая в вершину
, входящая в вершину  и принадлежащая по крайней мере двум путям из
и принадлежащая по крайней мере двум путям из  . Тогда в графе
. Тогда в графе 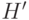 удалим одну дугу
удалим одну дугу 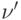 , соответствующую дуге
, соответствующую дуге 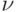 , и удалим одну замыкающую дугу, исходящую из
, и удалим одну замыкающую дугу, исходящую из  . Затем из начала дуги
. Затем из начала дуги 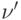 в вершину
в вершину  проведем одну дугу. Легко видеть, что полученный граф
проведем одну дугу. Легко видеть, что полученный граф 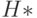 является эйлеровым и его эйлерову контуру соответствует покрытие графа
является эйлеровым и его эйлерову контуру соответствует покрытие графа  длины
длины 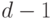 . Следовательно,
. Следовательно,  не является покрытием минимальной длины. Противоречие доказывает, что
не является покрытием минимальной длины. Противоречие доказывает, что  - минимально еопкрытие.
- минимально еопкрытие.
Рассмотрим, наконец, минимальное по длине покрытие 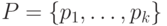 графа
графа  , у которого некоторые пути оканчиваются в
, у которого некоторые пути оканчиваются в  . Пусть кратность покрытия
. Пусть кратность покрытия  больше (8.1) и пути
больше (8.1) и пути 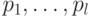 оканчиваются в
оканчиваются в  . Легко видеть, что покрытие
. Легко видеть, что покрытие  также является покрытием минимальной длины и все пути из
также является покрытием минимальной длины и все пути из 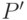 оканчиваются только в положительных вершинах. Выше было показано, что кратность покрытия
оканчиваются только в положительных вершинах. Выше было показано, что кратность покрытия 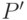 минимальна. Теорема доказана.
минимальна. Теорема доказана.
Перейдем к описанию алгоритма построения покрытия правильного графа  . Пути искомого покрытия обозначим через
. Пути искомого покрытия обозначим через 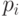 . Каждой вершине
. Каждой вершине  поставим в соответствие множество
поставим в соответствие множество 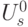 всех дуг, выходящих из
всех дуг, выходящих из  . Дуги в
. Дуги в 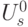 занумеруем числами
занумеруем числами  причем если
причем если  и
и  - петля, то
- петля, то  .
.
В алгоритме будут использованы функции 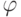 и
и 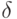 , определяемые такими соотношениями:
, определяемые такими соотношениями: 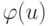 - номер дуги
- номер дуги  во множестве
во множестве 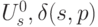 - конечная вершина пути
- конечная вершина пути  , исходящего из вершины
, исходящего из вершины  .
.
В описанном алгоритме кроме построения покрытия производится вычисление параметра 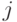 , необходимого для оценки длины полученного покрытия.
, необходимого для оценки длины полученного покрытия.
Для краткости при описании алгоритма используем операцию присваивания ":=", употребляемую в том же смысле, что и в алгоритмических языках.
-
 ; для всех
; для всех 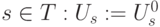 .
. - Если
 , то перейти к пункту 3, иначе к пункту 4.
, то перейти к пункту 3, иначе к пункту 4. -
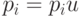 , где
, где  - дуга из множества
- дуга из множества 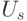 , имеющая наименьший номер;
, имеющая наименьший номер; 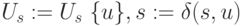 ; если
; если  , то
, то 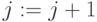 ; перейти к пункту 2.
; перейти к пункту 2. - Если
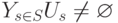 то перейти к пункту 5, иначе работа алгоритма завершается.
то перейти к пункту 5, иначе работа алгоритма завершается. - Если из вершины
 достижима хотя бы одна вершина
достижима хотя бы одна вершина  , для которой
, для которой 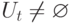 , то перейти к пункту 6, иначе к пункту 7.
, то перейти к пункту 6, иначе к пункту 7. - Построить кратчайший путь
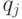 , ведущий из вершины
, ведущий из вершины  в вершину из множества
в вершину из множества 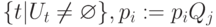 , и перейти к пункту 3.
, и перейти к пункту 3. -
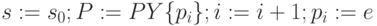 и перейти к пункту 3.
и перейти к пункту 3.
Заметим, что в случае сильно связного графа полученное по этому алгоритму покрытие имеет кратность 1.
Оценим сверху длину покрытия, построенного с помощью алгоритма  . Пусть
. Пусть 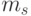 - мощность множества
- мощность множества 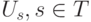 . Множество
. Множество  упорядочим отношением "
упорядочим отношением " 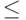 " и обозначим через
" и обозначим через 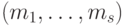 , где
, где  , если
, если 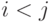 .
.
Алгоритм  можно считать пошаговым процессом, где
можно считать пошаговым процессом, где 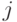 -м шагом будут являться построения, выполняемые алгоритмом при фиксированном значении параметра
-м шагом будут являться построения, выполняемые алгоритмом при фиксированном значении параметра 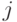 . Путь
. Путь 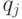 , описанный в пункте 6 алгоритма
, описанный в пункте 6 алгоритма  , будем называть транслирующим. Очевидно, что длина покрытия, построенного по алгоритму, равна сумме числа дуг графа и длин всех транслирующих путей.
, будем называть транслирующим. Очевидно, что длина покрытия, построенного по алгоритму, равна сумме числа дуг графа и длин всех транслирующих путей.
Оценим суммарную длину всех транслирующих путей покрытия, построенного по алгоритму  .
.
Из описанного алгоритма следует, что длина транслирующего пути 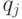 не превосходит числа таких вершин
не превосходит числа таких вершин  из
из 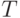 , для которых на
, для которых на 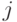 -м шаге
-м шаге 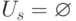 . Поэтому для значений
. Поэтому для значений 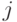 от 0 до
от 0 до 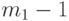 включительно
включительно 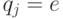 , где
, где  - "пустой" путь. Далее, для значений
- "пустой" путь. Далее, для значений 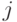 от
от  до
до 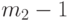 включительно длина
включительно длина 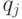 не превосходит единицы. Из описания алгоритма следует, что на последнем шаге работы алгоритма значение
не превосходит единицы. Из описания алгоритма следует, что на последнем шаге работы алгоритма значение 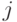 равно
равно 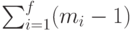 . Отсюда, учитывая предыдущие рассуждения, легко показать, что суммарная длина транслирующих путей, построенных по алгоритму, не превосходит величины
. Отсюда, учитывая предыдущие рассуждения, легко показать, что суммарная длина транслирующих путей, построенных по алгоритму, не превосходит величины
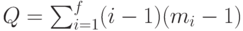 |
( 8.3) |
Следовательно, справедливо следующее утверждение.
Теорема 8.5. Для правильного графа  всегда существует покрытие, длина которого не превышает величины
всегда существует покрытие, длина которого не превышает величины
 |
( 8.4) |
где 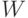 - число дуг графа.
- число дуг графа.
Следствие 1. Для правильного  -вершинного автоматного графа степени
-вершинного автоматного графа степени  всегда существует покрытие длины, не превышающей величины
всегда существует покрытие длины, не превышающей величины
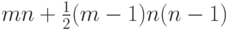 |
( 8.5) |
Следствие непосредственно вытекает из теоремы 8.5, так как для автоматного графа 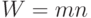 и
и 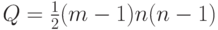 .
.
В [16] доказано, что для всех  и
и  существует
существует  -вершинный сильно связный автоматный граф степени
-вершинный сильно связный автоматный граф степени  , у которого имеется контур, проходящий через все дуги графа, минимальной длины, равной (8.5). Из этого факта следует, что оценка (8.5) достижима при всех
, у которого имеется контур, проходящий через все дуги графа, минимальной длины, равной (8.5). Из этого факта следует, что оценка (8.5) достижима при всех  и
и  . Следовательно, оценки (8.4) и (8.3) также достижимы.
. Следовательно, оценки (8.4) и (8.3) также достижимы.
Перейдем теперь к автоматной интерпретации полученных результатов. Если автомат Мили задан в виде конечного ориентированного автоматного графа, то каждому пути покрытия графа ставится в соответствие некоторое входное слово, а множество слов, соответствующих всем путям покрытия, составит кратный безусловный эксперимент. Таким образом, для распознавания функции выходов заданного инициального автомата или ему эквивалентного с  состояниями и
состояниями и  входными сигналами может быть использован кратный эксперимент , длина которого не превышает величины (8.5), а кратность - величины (8.2). Необходимое и достаточное условие существования кратного эксперимента, а также алгоритм его построения получаются простой переформулировкой теоремы 8.1 и алгоритма А.
входными сигналами может быть использован кратный эксперимент , длина которого не превышает величины (8.5), а кратность - величины (8.2). Необходимое и достаточное условие существования кратного эксперимента, а также алгоритм его построения получаются простой переформулировкой теоремы 8.1 и алгоритма А.
Вопросы и упражнения
- Приведите постановку задачи контроля функции выходов автомата с помощью кратного эксперимента.
- Приведите определение покрытия графа и его кратности.
- Каков критерий существований покрытия графа?
- Дайте определение приведенного покрытия графа.
- Приведите верхнюю и нижнюю оценки кратности для правильного не сильно связного графа.
- Дайте определение минимального покрытия графа.
- Каково условие существования минимального покрытия?
- Опишите процедуру построения покрытия правильного графа.