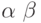Интервальная арифметика над конечным полем и ее приложения к теории экспериментов с автоматами
Заметим, что множество 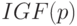 обобщенных интервалов является замкнутым относительно введенных бинарных операций.
обобщенных интервалов является замкнутым относительно введенных бинарных операций.
Как следует из формулы (19.4), любая бинарная операция над обобщенными интервалами сводится к соответствующей операции над обычными интервалами поля  .
.
Введем унарную операцию над обычным интервалом ![x=[\underline x,\bar x] \in IGF(p)](/sites/default/files/tex_cache/c8bd74efb45f59a506274ed87a7422d5.png) :
:
![-x=[-\underline x,-\bar x]](/sites/default/files/tex_cache/5f18e7fe16254c51cda41cd090f760f9.png)
где "  " - это элемент поля
" - это элемент поля  , обратный к элементу
, обратный к элементу  по сложению, т. е. такой, что
по сложению, т. е. такой, что 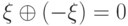 . Аналогичную операцию для обобщенного интервала
. Аналогичную операцию для обобщенного интервала 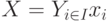 определим так:
определим так:

С использованием этой операции бинарная операция вычитания выражается через операцию сложения:
 |
( 19.5) |
Например, при ![p=5, a=[0,1], b=[4,1]](/sites/default/files/tex_cache/c91fd4aeed189ee647ca20d9cb87ded9.png) , тогда
, тогда ![[0,1] - [4,1] = [0,1] + (-[4,1]) = = [0,1] + [4,1] = [4,2]](/sites/default/files/tex_cache/010d0d788378fdff6a78b72633d9646b.png) .
.
Введем операцию умножения элемента  на обобщенный интервал
на обобщенный интервал  :
:
![\alpha \cdot X=Y_{\xi \in X}[\alpha \odot \xi, \alpha \odot \xi]](/sites/default/files/tex_cache/4745b0b6b661f3403398148e522a1239.png) |
( 19.6) |
Используя эту операцию, бинарную операцию умножения обобщенных интервалов можно записать в виде
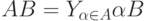 |
( 19.7) |
Например, если ![p=5, а=[2,4], b=[1,2]](/sites/default/files/tex_cache/a3ca9f8f57d6fc880b724695293491b8.png) то имеем
то имеем
![a \cdot b=2[1,2] \bigcup 3[1,2]\bigcup 4[1,2]=[2,2]\bigcup [4,4]\bigcup [3,3]\bigcup [1,1] \bigcup [3,4]=[1,4]](/sites/default/files/tex_cache/7b49e63c430498c3d3bda6a9e65f9d45.png)
И наконец, операцию деления обобщенных интервалов можно записать в виде
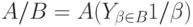 |
( 19.8) |
где 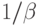 - это элемент
- это элемент  , обратный элементу
, обратный элементу  по умножению, т. е. такой, что
по умножению, т. е. такой, что 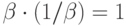 .
.
Например, если ![p=5, a=[1,3], b=[3,4]](/sites/default/files/tex_cache/d4b94be99c272beaf5f1e0503ed9815a.png) , то
, то
![[1,3]/[3,4]=[1,3](1/3 \bigcup 1/4)= [1,3]*(2 \bigcup 4)=2*[1,3]\bigcup 4*[1,3]=[1,2] \bigcup [4,4]\bigcup [2,4]=[1,4].](/sites/default/files/tex_cache/8587f3371820aa955822a05d9fb0799f.png)
Остановимся на свойствах арифметических операций в 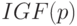 . Напомним, что в классической интервальной арифметике [2] функция
. Напомним, что в классической интервальной арифметике [2] функция
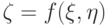
где  (при делении предполагается, что
(при делении предполагается, что 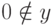 ) - непрерывные функции на компактном множестве, и потому
) - непрерывные функции на компактном множестве, и потому 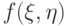 принимает как наименьшее, так и наибольшее значения. Таким образом,
принимает как наименьшее, так и наибольшее значения. Таким образом,  есть также замкнутый вещественный интервал, который полностью заполнен вещественными числами, являющимися результатами упомянутых бинарных операций над соответствующими числами. При этом границы результата выражаются через операции с границами операндов. Некоторая, но не полная, аналогия справедлива и в интервальной арифметике над полем
есть также замкнутый вещественный интервал, который полностью заполнен вещественными числами, являющимися результатами упомянутых бинарных операций над соответствующими числами. При этом границы результата выражаются через операции с границами операндов. Некоторая, но не полная, аналогия справедлива и в интервальной арифметике над полем  . Исходя из указанной аналогии, найдем формулы, позволяющие выражать результаты бинарных операций над обычными интервалами через их границы.
. Исходя из указанной аналогии, найдем формулы, позволяющие выражать результаты бинарных операций над обычными интервалами через их границы.
Введем понятие ширины обобщенного интервала 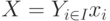 и обычного интервала
и обычного интервала ![x_i=[\underline x_i, \bar x_i]](/sites/default/files/tex_cache/6a98c16ae070896319f08b057c30cb30.png) , обозначаемых далее как
, обозначаемых далее как  и
и 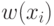 соответственно:
соответственно:
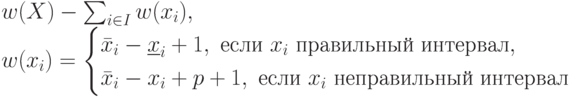
Понятно, что 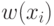 и
и  - это число элементов в соответствующих интервалах. Очевидно также, что
- это число элементов в соответствующих интервалах. Очевидно также, что 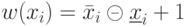 в любом случае.
в любом случае.
Пусть ![a=[\underline a, \bar a], b=[\underline b, \bar b]](/sites/default/files/tex_cache/2a1c44c00da91fbbc99e27d7a396b6bf.png) - обычные интервалы поля
- обычные интервалы поля  , тогда для сложения интервалов справедлива следующая формула
, тогда для сложения интервалов справедлива следующая формула
![a+b=
\left \{
\bedin {matrix}
[\underline a \oplus \bar b, \bar a \oplus \underline b], \qquad \mbox{если} \qquad w(a)+w(b) \le p,\\
[0, p-1] \qquad \mbox{в противном случае} \qquad
\end {matrix}](/sites/default/files/tex_cache/d36b4b98dcf508ef382eb762bffcf5a6.png)
Доказательство этой формулы приведено в [31].
Аналогично, для операции вычитания обычных интервалов справедлива следующая формула
![a-b=
\left \{
\begin {matrix}
[\underline a \circleddash \bar b, \bar a \circleddash b], \ \mbox {если} \ w(a)+w(b) \le p,\\
[0, p-1] \ \mbox {в противном случае} \qquad
\end {matrix}](/sites/default/files/tex_cache/2d49da2a9eec7375024ad7996c132e4f.png)
Произведение и частное интервалов представить через операции с границами сомножителей в общем случае не удается. Ситуация по сравнению с классической интервальной арифметикой осложняется в связи с тем, что, к примеру, для произведения интервалов не выполняется даже включение: ![ab \subseteq [\underline a \odot \underline b, \bar a \odot \bar b].](/sites/default/files/tex_cache/100fdc85c3dfafee3580d5e2e5476521.png)
Следующее утверждение, доказательство которого приведено в [31], касается свойств введенных интервальных операций и самих интервалов.
Теорема 19.1. Пусть  , тогда:
, тогда:
-
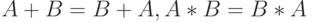 (коммутативность);
(коммутативность); -
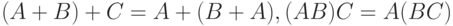 (ассоциативность);
(ассоциативность); -
![(\forall A \in IGF(p)) A=A+[0,0]=[0,0]+A, A*[1,1]=[1,1]*A](/sites/default/files/tex_cache/a389cc339a2f8acaa9c0ee429d1d903e.png) , то есть
, то есть ![[0,0]](/sites/default/files/tex_cache/e013e067435150802e1c67877ce69879.png) и
и ![[1,1]](/sites/default/files/tex_cache/3010237bcb5be77d69ea2a1e48891637.png) являются единственными нейтральными элементами для сложения и умножения соответственно;
являются единственными нейтральными элементами для сложения и умножения соответственно; -
 не имеет делителей нуля;
не имеет делителей нуля; - Произвольный невырожденный интервал из
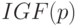 не имеет обратного ни по сложению, ни по умножению, но
не имеет обратного ни по сложению, ни по умножению, но 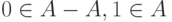 ;
; -
 (субдистрибутивность);
(субдистрибутивность); -
 , где
, где  (дистрибутивность умножения на число);
(дистрибутивность умножения на число); -
![\forall \alpha \in GF(p) [\alpha, \alpha -1]=[0, p-1]](/sites/default/files/tex_cache/d48f2581be42bea6c2e7d5b260f2acd0.png) ;
; -
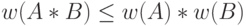 , где
, где 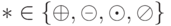 ;
; -
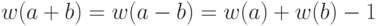 если
если 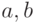 - обычные интервалы и
- обычные интервалы и 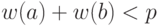 ;
; -
 и
и  .
.
Заметим, что 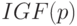 с введенными операциями сложения и умножения на число не является линейным пространством, и даже квазилинейным, так как не выполняется аксиома линейности
с введенными операциями сложения и умножения на число не является линейным пространством, и даже квазилинейным, так как не выполняется аксиома линейности
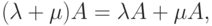
где
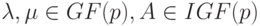
Как и в классической интервальной арифметике, в интервальной арифметике над конечным полем  возникают задачи поиска решений интервальных уравнений и систем. Кратко остановимся на этом.
возникают задачи поиска решений интервальных уравнений и систем. Кратко остановимся на этом.
Рассмотрим уравнение относительно Х
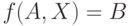 |
( 19.9) |
зависящее от некоторых параметров  , где
, где 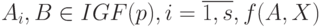 - рациональное выражение, которое состоит из интервалов
- рациональное выражение, которое состоит из интервалов  соединенных знаками арифметических операций.
соединенных знаками арифметических операций.
Определение 19.4. Назовем алгебраическим решением уравнения (19.9) такой обобщенный интервал  , что при его подстановке в (19.9) получается точное равенство.
, что при его подстановке в (19.9) получается точное равенство.
Пусть, например,  и рассматривается уравнение
и рассматривается уравнение ![[1,2]+X=[4,2]](/sites/default/files/tex_cache/16537cbde9200e3ac00a63c23815fd5c.png) . Можно убедиться, что интервалы
. Можно убедиться, что интервалы ![X_1=[0,0] \bigcup [3,3]](/sites/default/files/tex_cache/a92fb87d4489eef7fb8c248d1250339a.png) и
и ![X_2=[3,0] ([3,0]=[0,0] \bigcup [3,3] \bigcup [4,4])](/sites/default/files/tex_cache/0543683bfc77f0d359ae487c5379dd5d.png) , подставленные в заданное уравнение, дают точное равенство, т. е. оба этих интервала являются алгебраическими решениями. Из этого примера следует, что алгебраическое решение уравнения
, подставленные в заданное уравнение, дают точное равенство, т. е. оба этих интервала являются алгебраическими решениями. Из этого примера следует, что алгебраическое решение уравнения 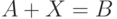 в общем случае не единственно.
в общем случае не единственно.
Следующие определения множеств решений были введены в [51] для множеств решений интервальных систем линейных алгебраических уравнений, здесь эти множества решений определяются для уравнений (19.9).
Определение 19.5. Назовем объединенным множеством решений уравнения (19.9) следующее множество элементов:
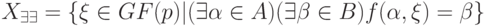
Так, для уравнения ![[1,2]+X=[4,2]](/sites/default/files/tex_cache/16537cbde9200e3ac00a63c23815fd5c.png) объединенное множество решений есть
объединенное множество решений есть ![X_{\exists \exists }=[0,4]](/sites/default/files/tex_cache/dd5718eb35254b75e122a6233b51d913.png) .
.
Определение 19.6. Назовем допустимым множеством решений уравнения (5.9) следующее множество:
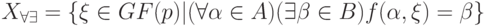
Для рассмотренного выше примера ![X_{\forall \exists }=[3,0]](/sites/default/files/tex_cache/e235f5560dfc78fc66007428d7e2595a.png) , т. е. для этого уравнения имеет место включение
, т. е. для этого уравнения имеет место включение 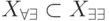 . Легко показать, что такое включение справедливо и в общем случае. Кроме того, для этого же примера
. Легко показать, что такое включение справедливо и в общем случае. Кроме того, для этого же примера 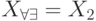 , т. е. допустимое множество решений совпадает с одним из алгебраических решений.
, т. е. допустимое множество решений совпадает с одним из алгебраических решений.
Определение 19.7. Назовем управляемым множеством решений уравнения (19.9) следующее множество:
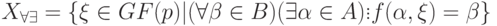
Так, для  уравнение
уравнение ![[1,3]+X=[0,1]](/sites/default/files/tex_cache/bb147c96e351868307d30c71c4434bd0.png) управляемое множество решений есть
управляемое множество решений есть ![X_{\exists \forall }=[3,4]](/sites/default/files/tex_cache/96091943b57857dc03f6553e08d0cd63.png) .
.
Теорема 19.2. Линейное уравнение 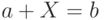 , где
, где 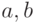 - обычные интервалы над полем
- обычные интервалы над полем  , имеет алгебраическое решение
, имеет алгебраическое решение  в виде обобщенного интервала тогда и только тогда, когда
в виде обобщенного интервала тогда и только тогда, когда  .
.
Доказательство.
Необходимость. Докажем ее от противного. Пусть 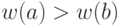 . Покажем, что в этом случае рассматриваемое уравнение решений не имеет. Пусть
. Покажем, что в этом случае рассматриваемое уравнение решений не имеет. Пусть 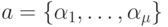 . Выберем произвольный элемент
. Выберем произвольный элемент  и построим множество
и построим множество 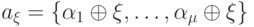 . Очевидно, что в
. Очевидно, что в 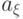 все элементы попарно различны т. е.
все элементы попарно различны т. е. 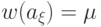 . Элемент
. Элемент 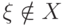 поскольку среди элементов
поскольку среди элементов 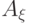 существует по крайней мере один такой элемент
существует по крайней мере один такой элемент 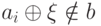 ибо
ибо 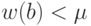 . Из произвольности элемента
. Из произвольности элемента  следует, что в
следует, что в  нет ни одного элемента
нет ни одного элемента 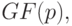 т. е. алгебраическое решение пусто.
т. е. алгебраическое решение пусто.
Достаточность. Пусть  тогда алгебраическое решение есть
тогда алгебраическое решение есть ![X=[\underline b \circleddash \underline a, \bar b \circleddash \bar a], a+X=[a,a]+[ \underline b \circleddash \underline a, \bar b \circleddash \bar a]= \underline a \oplus \underline b \circleddash \underline a, \bar a \oplus \bar b \circleddash \bar a]=[ \underline b, \bar b]=b](/sites/default/files/tex_cache/800013b5ded9e723abdecf25e7e35da5.png) . При этом по свойству 11 в теореме 19.1
. При этом по свойству 11 в теореме 19.1  . Отсюда следует, что
. Отсюда следует, что 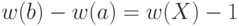 Тогда, учитывая, что
Тогда, учитывая, что  , получим
, получим 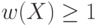 , т. е. множество
, т. е. множество  не пусто.
не пусто.
Заметим, что теорема 19.2 для случая, когда в уравнении 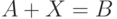 вместо обычных интервалов использованы обобщенные интервалы, неверна. В самом деле, пусть
вместо обычных интервалов использованы обобщенные интервалы, неверна. В самом деле, пусть ![p=7, A+[1,1] \bigcup [3,3] \bigcup [5,5], B+[6,2]](/sites/default/files/tex_cache/aac9ad28372f0862dbfc9f6c2cf2712a.png) . Перебором можно проверить, что уравнение в этом случае алгебраического решения не имеет.
. Перебором можно проверить, что уравнение в этом случае алгебраического решения не имеет.
Для существования алгебраического решения уравнения 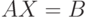 условие
условие  является необходимым, но не является достаточным даже для случая, когда
является необходимым, но не является достаточным даже для случая, когда  и
и  - обычные интервалы. Например, при
- обычные интервалы. Например, при  уравнение
уравнение ![[2,4]*X=[2,5]](/sites/default/files/tex_cache/10a262310a2b24259d6190126fdcbd47.png) алгебраического решения не имеет, хотя
алгебраического решения не имеет, хотя 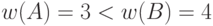 . В то же время это уравнение имеет объединенное множество решений
. В то же время это уравнение имеет объединенное множество решений ![X_{\exists \exists }=[1,6]](/sites/default/files/tex_cache/df83bbb6babe02fd37f2e1fedaed7f22.png) и допустимое множество решений
и допустимое множество решений ![X_{\forall \exists }=[1,1] \bigcup [6,6]](/sites/default/files/tex_cache/4bf17d9a5298da06210fc77567572aea.png) .
.
Для уравнения
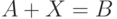
введенные множества решений определяются следующим образом:
 |
( 19.10) |
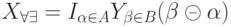 |
( 19.11) |
 |
( 19.12) |
Для уравнения
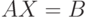
где

множество решений определяются аналогично:
 |
( 19.13) |
 |
( 19.14) |
 |
( 19.15) |
Равенства (19.10)-(19.12), (19.13)-(19.15) следуют из определения множеств 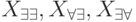 и определения теоретико-множественных операций объединения и пересечения.
и определения теоретико-множественных операций объединения и пересечения.
Рассмотрим пример. Пусть  и уравнение имеет вид
и уравнение имеет вид
![[2,4]*X=[2,5]](/sites/default/files/tex_cache/10a262310a2b24259d6190126fdcbd47.png)
Для наглядности построим таблицу деления  , где
, где ![\beta \in [2,5], \alpha \in [2,4]](/sites/default/files/tex_cache/3cf83680400f6a056765e8ee3e1ea32c.png) .
.
Объединение всех элементов строк (столбцов) таблицы составляет объединенное множество решений ![X_{\exists \exists}=[1,6]](/sites/default/files/tex_cache/b62564267d24866a501ce5d35b2d03eb.png) . Пересечение элементов строк таблицы составляет допустимое множество решений
. Пересечение элементов строк таблицы составляет допустимое множество решений ![X_{\forall \exists }=[1,1] \bigsup [6,6]](/sites/default/files/tex_cache/4f08fc044c97cbe56c2064e37d3038b4.png) . Пересечение элементов столбцов таблицы пусто, поэтому
. Пересечение элементов столбцов таблицы пусто, поэтому 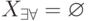 и управляемых решений уравнение не имеет.
и управляемых решений уравнение не имеет.
Теорема 19.3. Все множество решений уравнений 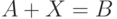 и
и 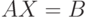 и алгебраическое решение, если оно существует, включаются в объединенное множество решений, т. е. в
и алгебраическое решение, если оно существует, включаются в объединенное множество решений, т. е. в  для уравнения
для уравнения 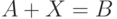 и в
и в  для уравнения
для уравнения 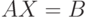
Доказательство этой теоремы следует из равенств (19.10)-(19.12), (19.13)-(19.15) для множеств решений. Для алгебраического решения очевидно, что если оно существует, то все его элементы являются допустимыми решениями и, следовательно, принадлежат также и объединенному множеству решений.
Вопросы и упражнения
- Дайте определение равенства двух интервалов.
- Приведите определения различных типов интервалов: обычных, обобщенных, правильных, неправильных, вырожденных.
- Дайте определение бинарных операций над различными типами интервалов.
- Перечислите свойства интервалов и операций над ними.
- Приведите определения различных типов решений интервального уравнения
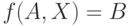 : алгебраического, объединенного, допустимого, управляемого.
: алгебраического, объединенного, допустимого, управляемого. - Сформулируйте критерий существования алгебраического решения линейного интервального уравнения
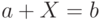 .
.