Диагностическая задача в интервальной постановке
При таком выборе целевая функция будет неотрицательной во всей области допустимых значений и принимать значение 0 лишь на решениях интервальной диагностической задачи.
Однако в классическом понимании целевой функции как функции приспособленности необходимо, чтобы более приспособленные особи оценивались выше, чем менее приспособленные. Этого легко достичь, если произвести нормализацию целевой функции и обратить ее:
 |
( 20.11) |
где
 |
( 20.12) |
Таким образом, целевая функция  будет принимать значения в диапазоне от 0 до 1. При этом большему значению целевой функции соответствует большая степень приспособленности хромосомы, т. е. данная целевая функция является "истинно" функцией приспособленности. Очевидно, что на решениях интервальной диагностической задачи целевая функция будет принимать значение 1.
будет принимать значения в диапазоне от 0 до 1. При этом большему значению целевой функции соответствует большая степень приспособленности хромосомы, т. е. данная целевая функция является "истинно" функцией приспособленности. Очевидно, что на решениях интервальной диагностической задачи целевая функция будет принимать значение 1.
Теперь коснемся вопроса определения вероятностей применения операторов ПГА. Как же их определять? На этот вопрос пока нет простого и однозначного ответа. В докторской диссертации де Джонга (1975), посвященной исследованию генетических алгоритмов, отмечается, что для хорошей работы ГА необходимо выбирать большую вероятность кроссинговера и малую вероятность мутации (например, обратно пропорционально размеру популяции). Следует заметить, что это правило не всегда оправдывает себя, например, для областей, связанных с исследованиями социальных адаптивных систем. Однако в большинстве технических задач это правило работает, и мы в нашей работе будем его использовать.
Размер популяции и максимальное количество поколений определяют объем вычислений программы. Чем они больше, тем больше вычислений проводится и большее количество хромосом будет просмотрено в поисках решения. Очевидно, что эти параметры надо делать максимальными. Однако с ростом этих параметров растет и время работы программы. Поэтому выбор их в большей степени определяется вычислительной мощностью и предельным временем, за которое программа должна найти решение.
В ходе исследования поставленной интервальной диагностической задачи была написана программа, которая решает эту задачу. Основу программы представляет реализация простого генетического алгоритма на языке C. Эта реализация имеет имя SGA-C v. 1.1 (Simple Genetic Algorithm on C), и представляет собой интерпретацию кода из книги Goldberg D.E. "Genetic Algorithms in Search, Optimization, and Machine Learning" (1989) на языке C.
SGA-C реализует простой генетический алгоритм , который содержит операторы отбора, скрещивания и мутации, и механизм задания вероятности применения этих операторов. При этом SGA-C позволяет исследователю сделать настройку для решения его специфических задач с помощью набора функций в файле app.c. Для решения поставленной интервальной диагностической задачи были написаны следующие функции:
- Функция начальной инициализации пользовательских данных: производит считывание основных параметров (характеристики поля
 , длины диагностической последовательности), характеристических матриц ЛА, входных и выходных векторов.
, длины диагностической последовательности), характеристических матриц ЛА, входных и выходных векторов. - Функция приспособленности objfunc (): производит вычисление функции
 по формулам (20.10)-(20.12).
по формулам (20.10)-(20.12). - Функция отчета app_report (): производит печать всех найденных в ходе работы программы решений и их количества.
- Функция chrom2matrix (): производит декодирование хромосомы в матрицу.
- Функции matrix_sum (), matrix_mult (): реализуют операции сложения и умножения матриц.
Эта программа для нахождения решения интервальной диагностической задачи на основе генетического алгоритма размещена в Интернете по адресу: http://menace.cs.sgu.ru/sam/genetic/download/sga-c.auto.zip .
Рассмотрим ряд примеров решения сформулированной диагностической задачи с применением данной программы.
Пример 2.
Решим интервальную диагностическую задачу для ЛА из примера 1.
Согласно описанной выше рекомендации, вероятность оператора кроссинговера 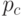 положим равной 0.1, а вероятность оператора мутации
положим равной 0.1, а вероятность оператора мутации  . Пусть популяция состоит из 20 хромосом, длина хромосомы равна 9 и максимальное количество поколений равно 100. При таких параметрах генетического алгоритма программой было найдено решение:
. Пусть популяция состоит из 20 хромосом, длина хромосомы равна 9 и максимальное количество поколений равно 100. При таких параметрах генетического алгоритма программой было найдено решение: ![s(0)=[105]^T](/sites/default/files/tex_cache/4d3fc217628c16f92a52c059eb51d5b0.png) . Как уже известно (пример 1), это решение является искомым решением интервальной диагностической задачи.
. Как уже известно (пример 1), это решение является искомым решением интервальной диагностической задачи.
Как было сказано выше, вероятности операторов играют большую роль при работе генетического алгоритма. Чтобы проиллюстрировать это, данная задача решалась при разных вероятностях оператора скрещивания ( 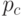 ) и оператора мутации (
) и оператора мутации ( 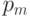 ). В представленной ниже таблице содержится информация о нахождении решения интервальной диагностической задачи для разных значений
). В представленной ниже таблице содержится информация о нахождении решения интервальной диагностической задачи для разных значений 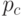 и
и 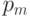 (в клетке таблицы стоит 0, если решение не найдено, 1 - если найдено).
(в клетке таблицы стоит 0, если решение не найдено, 1 - если найдено).
Из этой таблицы можно сделать следующие выводы:
- для малых значений вероятности мутации (0.00-0.02) решение задачи находится далеко не всегда, что является свидетельством необходимости участия мутации в процессе работы генетического алгоритма;
- для достаточно большого числа наборов пар вероятностей (89 из 121, т. е. в 73 % случаев) алгоритм находит решение интервальной диагностической задачи.
 |
0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | 0.10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0.05 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0.10 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.15 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.20 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.25 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.30 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.35 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.40 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.45 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.50 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
Пример 3.
Рассмотрим ЛА из примера 1. Входные векторы оставим без изменений, а выходные векторы сделаем точными, т. е. рассмотрим случай вырожденных интервалов:
![y(0)=
\left [
\begin {matrix}
[3,3]\\
[4,4]
\end {matrix}
\right ],
y(1)=
\left [
\begin {matrix}
[1,1]\\
[3,3]
\end {matrix}
\right ],
y(2)=
\left [
\begin {matrix}
[5,5]\\
[5,5]
\end {matrix}
\right ]](/sites/default/files/tex_cache/f3e224f8d501b846a62edf72d3d4b14c.png)
Заметим, что хотя выходные векторы заданы с помощью интервалов, однако представляют собой векторы с точными значениями. Таким образом, данный пример является примером классической диагностической задачи.
Используя таблицу из примера 2, положим вероятность оператора кроссинговера 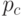 равной 0.15, а вероятность оператора мутации
равной 0.15, а вероятность оператора мутации 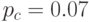 . Пусть популяция состоит из 20 хромосом и максимальное количество поколений равно 200. При таких параметрах генетического алгоритма программой было найдено следующее решение:
. Пусть популяция состоит из 20 хромосом и максимальное количество поколений равно 200. При таких параметрах генетического алгоритма программой было найдено следующее решение: ![s(0)=[4 5 6]^T](/sites/default/files/tex_cache/50f157ed809fc17214c2c8b03628222d.png) . Найденное решение является одним из допустимых начальных состояний заданного ЛА, поэтому классическая диагностическая задача имеет решение, и это решение есть
. Найденное решение является одним из допустимых начальных состояний заданного ЛА, поэтому классическая диагностическая задача имеет решение, и это решение есть  .
.
Таким образом, пример 3 иллюстрирует тот факт, что генетический алгоритм позволяет решать диагностическую задачу как в интервальной постановке, так и в классическом случае.
Главными преимуществами генетического алгоритма при решении разнообразных задач являются небольшой объем используемой памяти и высокая скорость получения решения. Например, при 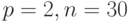 , программа с применением ГА нашла решение менее чем за 1 секунду своей работы (был взят компьютер с процессором Celeron 900 MHz). Другая программа, которая осуществляла поиск решения полным перебором, это же решение нашла только через несколько десятков часов при использовании того же компьютера. Таким образом, генетический подход к решению интервальной диагностической задачи не уступает точному алгебраическому подходу как по скорости, так и по качеству решения поставленной задачи.
, программа с применением ГА нашла решение менее чем за 1 секунду своей работы (был взят компьютер с процессором Celeron 900 MHz). Другая программа, которая осуществляла поиск решения полным перебором, это же решение нашла только через несколько десятков часов при использовании того же компьютера. Таким образом, генетический подход к решению интервальной диагностической задачи не уступает точному алгебраическому подходу как по скорости, так и по качеству решения поставленной задачи.
Вопросы и упражнения
- Сформулируйте диагностическую задачу для линейного автомата в интервальной постановке.
- Опишите метод построения интервального диагностического дерева для ЛА с заданным множеством допустимых начальных состояний.
- Укажите способ сведения решения задачи о поиске неизвестного начального состояния ЛА в интервальной постановке к решению системы линейных уравнений с интервальной правой частью.
- Сформулируйте теорему о виде решения системы
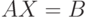 c интервальной правой частью.
c интервальной правой частью. - Опишите идею построения генетического алгоритма для решения диагностической задачи для ЛА в интервальной постановке.
- Приведите вид целевой функции, используемой в описанном генетическом алгоритме.
