Минимизация времени восстановления неизвестных входных сигналов в сети из автоматов без потери информации
Лемма 17.3. Величина максимального потока в порожденной сети 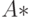 равна числу
равна числу  внешних входов исходной сети
внешних входов исходной сети  .
.
Доказательство. Рассмотрим разрез 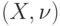 сети
сети 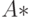 , где
, где  - множество всех вершин порожденной сети, исключая вершину
- множество всех вершин порожденной сети, исключая вершину  . Поскольку пропускная способность каждой дуги этого разреза равна 1, а из правил построения порожденной сети следует, что число дуг, входящих в разрез
. Поскольку пропускная способность каждой дуги этого разреза равна 1, а из правил построения порожденной сети следует, что число дуг, входящих в разрез 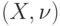 , равно числу
, равно числу  первичных входов исходной сети, то пропускная способность этого разреза равна
первичных входов исходной сети, то пропускная способность этого разреза равна  . Из правил построения порожденной сети следует, что никакой другой разрез порожденной сети не может содержать дуг меньше, чем
. Из правил построения порожденной сети следует, что никакой другой разрез порожденной сети не может содержать дуг меньше, чем  . Отсюда на основании теоремы о максимальном потоке и минимальном разрезе [34] вытекает справедливость леммы.
. Отсюда на основании теоремы о максимальном потоке и минимальном разрезе [34] вытекает справедливость леммы.
Лемма 17.4. Множеству всех увеличивающих цепей в порожденной сети 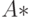 , обеспечивающих максимальное значение потока минимальной стоимости, соответствует покрывающее множество путей в исходной сети
, обеспечивающих максимальное значение потока минимальной стоимости, соответствует покрывающее множество путей в исходной сети  с минимальным временем восстановления входного вектора.
с минимальным временем восстановления входного вектора.
Доказательство. Пусть в порожденной сети построен максимальный поток  , имеющий минимальную стоимость, который проходит по множеству увеличивающих цепей
, имеющий минимальную стоимость, который проходит по множеству увеличивающих цепей 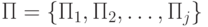 . Из леммы 17.3 и того факта, что все дуги вида
. Из леммы 17.3 и того факта, что все дуги вида 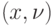 в порожденной сети имеют пропускную способность 1, следует, что число
в порожденной сети имеют пропускную способность 1, следует, что число  увеличивающих цепей в
увеличивающих цепей в  должно равняться
должно равняться  . Действительно, если на
. Действительно, если на  -м шаге процесса решения задачи о потоке минимальной стоимости построена увеличивающая цепь, последняя дуга которой есть
-м шаге процесса решения задачи о потоке минимальной стоимости построена увеличивающая цепь, последняя дуга которой есть 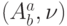 , то все другие увеличивающие цепи, появляющиеся в процессе решения на последующих шагах работы алгоритма, не могут содержать дуги
, то все другие увеличивающие цепи, появляющиеся в процессе решения на последующих шагах работы алгоритма, не могут содержать дуги 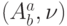 . Это объясняется тем, что после
. Это объясняется тем, что после  -го шага дуга
-го шага дуга 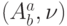 является насыщенной и потому в дальнейшем она блокирует появление увеличивающих цепей, проходящих через нее.
является насыщенной и потому в дальнейшем она блокирует появление увеличивающих цепей, проходящих через нее.
Рассмотрим произвольную цепь 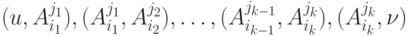 из множества
из множества  . Поставим ей в соответствие путь в исходной сети
. Поставим ей в соответствие путь в исходной сети 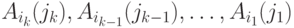 , где
, где 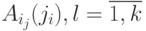 , означает входной (или, что все равно, выходной) полюс
, означает входной (или, что все равно, выходной) полюс 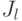 автомата-компонента
автомата-компонента 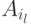 исходной сети. Из способа построения порожденной сети следует, что
исходной сети. Из способа построения порожденной сети следует, что  является внешним входом (выходом) сети. Таким образом, приведенный путь указывает перечень входов автоматов-компонентов исходной сети и тот порядок, в котором следует восстанавливать сигналы на них с тем, чтобы в конечном итоге восстановить сигнал на внешнем входе сети. Поскольку среди конечных вершин множества упомянутых путей обязательно имеются все внешние входы исходной сети, то по определению оно является покрывающим. Очевидно, что в силу минимальной стоимости потока общее время восстановления входного вектора, осуществляемое вдоль путей построенного покрывающего множества, будет минимальным.
является внешним входом (выходом) сети. Таким образом, приведенный путь указывает перечень входов автоматов-компонентов исходной сети и тот порядок, в котором следует восстанавливать сигналы на них с тем, чтобы в конечном итоге восстановить сигнал на внешнем входе сети. Поскольку среди конечных вершин множества упомянутых путей обязательно имеются все внешние входы исходной сети, то по определению оно является покрывающим. Очевидно, что в силу минимальной стоимости потока общее время восстановления входного вектора, осуществляемое вдоль путей построенного покрывающего множества, будет минимальным.
Леммы 17.3 и 17.4 служат обоснованием метода решения рассматриваемой задачи, состоящего из трех этапов. На первом этапе по заданной сети из ЛА БПИ строится порожденная ею сеть. Второй этап состоит в решении известным методом, описанным, например, в [34], задачи о потоке величины  минимальной стоимости, где
минимальной стоимости, где  - число внешних входов исходной сети. На третьем этапе по найденному в процессе решения на втором этапе множеству увеличивающих цепей строится искомое множество покрывающих путей.
- число внешних входов исходной сети. На третьем этапе по найденному в процессе решения на втором этапе множеству увеличивающих цепей строится искомое множество покрывающих путей.
Проиллюстрируем предложенный метод на примере сети из ЛА БПИ, неизбыточных по выходам, которая изображена на рис.17.1
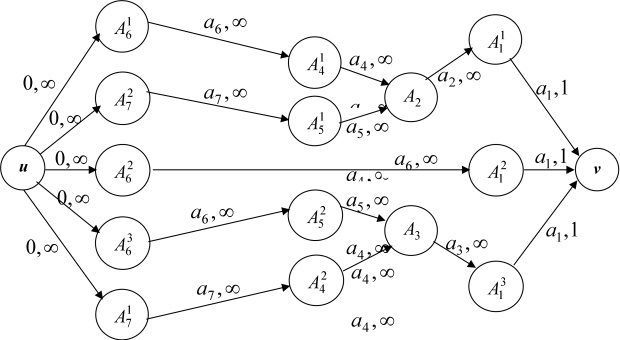
Построим по описанным выше правилам порожденную сеть, изображенную на рис.17.2.
Каждой дуге этой сети поставим в соответствие упорядоченную пару чисел, из которых первое является весовым коэффициентом, а второе - пропускной способностью. Правила назначения дугам упомянутых значений описаны выше. Весовые коэффициенты на дугах рис.17.2 обозначены числами 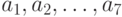 . Пусть для рассматриваемого примера эти значения таковы:
. Пусть для рассматриваемого примера эти значения таковы:  . Теперь приступим к решению задачи о максимальном потоке (для заданной сети его величина равна 3, поскольку сеть имеет 3 внешних входа) минимальной стоимости, воспользовавшись методом, описанным в [34]. Процесс решения отображен в приведенной таблице 17.1, которую кратко прокомментируем.
. Теперь приступим к решению задачи о максимальном потоке (для заданной сети его величина равна 3, поскольку сеть имеет 3 внешних входа) минимальной стоимости, воспользовавшись методом, описанным в [34]. Процесс решения отображен в приведенной таблице 17.1, которую кратко прокомментируем.
Столбцы этой таблицы со 2-го по 17-й соответствуют вершинным числам 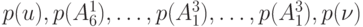 , которым на нулевом шаге присваивается значение 0. Перед началом работы окрашенным считается только исток сети, т. е. вершина
, которым на нулевом шаге присваивается значение 0. Перед началом работы окрашенным считается только исток сети, т. е. вершина  . Поскольку на всех дугах, исходящих из вершины
. Поскольку на всех дугах, исходящих из вершины  , стоимость прохождения единицы потока равна 0, имеют место равенства
, стоимость прохождения единицы потока равна 0, имеют место равенства  . Поэтому окрашиваются дуги, перечень которых приведен в столбце 18 таблицы нулевого шага, а также концевые вершины этих дуг (столбец 19). Теперь перейдем к следующему шагу. Для всех неокрашенных вершин увеличиваем вершинные числа на 1, что отражено во 2-й строке таблицы (шаг 1). Однако на этом шаге перечень окрашенных дуг и вершин остается прежним, так как теперь ни для каких других пар вершин разность их вершинных чисел не совпадает со "стоимостью" на соответствующей дуге.
. Поэтому окрашиваются дуги, перечень которых приведен в столбце 18 таблицы нулевого шага, а также концевые вершины этих дуг (столбец 19). Теперь перейдем к следующему шагу. Для всех неокрашенных вершин увеличиваем вершинные числа на 1, что отражено во 2-й строке таблицы (шаг 1). Однако на этом шаге перечень окрашенных дуг и вершин остается прежним, так как теперь ни для каких других пар вершин разность их вершинных чисел не совпадает со "стоимостью" на соответствующей дуге.
| № стр | 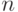 |
 |
 |
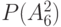 |
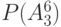 |
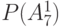 |
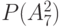 |
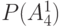 |
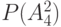 |
 |
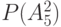 |
 |
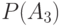 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 5 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 3 | 3 |
| 6 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 4 | 4 |
| 7 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 4 | 4 |
| 8 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 4 | 4 |
| 9 | - | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 4 | 4 |
| 10 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 4 | 4 |
| 11 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 4 | 4 |
| 12 | - | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 4 | 4 |
| 13 | - | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 2 | 3 | 4 | 4 |
Продолжение таблицы
| № стр | 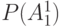 |
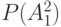 |
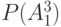 |
 |
Окрашенные дуги | Окрашенные вершины |
|---|---|---|---|---|---|---|
| 1 | 14 | 15 | 16 | 17 | 18 | 19 |
| 2 | 0 | 0 | 0 | 0 | 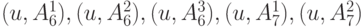 |
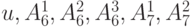 |
| 3 | 1 | 1 | 1 | 1 | те же | те же |
| 4 | 2 | 2 | 2 | 2 | те же 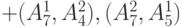
|
те же 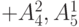
|
| 5 | 3 | 3 | 3 | 3 | те же 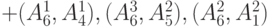
|
те же 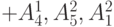
|
| 6 | 5 | 3 | 5 | 5 | те же 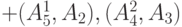
|
те же 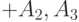
|
| 7 | 5 | 3 | 5 | 5 | те же 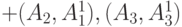
|
те же 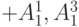
|
| 8 | 5 | 3 | 5 | 5 | те же 
|
те же 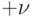
|
| 9 | 5 | 3 | 5 | 6 | нет |  |
| 10 | 5 | 3 | 5 | 7 | все, исключая 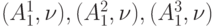
|
все, исключая 
|
| 11 | 5 | 3 | 5 | 8 | те же 
|
все |
| 12 | 5 | 3 | 5 | 8 | нет |  |
| 13 | 5 | 3 | 5 | 8 | все, исключая 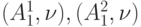
|
все |
Далее процесс продолжается аналогичным образом до 6-го шага включительно. На этом шаге из окрашенных дуг может быть построена увеличивающая цепь 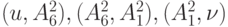 , по которой поток может быть увеличен на 1. Напомним, что в соответствии с используемым методом из [34] перед началом его работы значения потоков на всех дугах сети полагаются равными 0. Поскольку на 6-м шаге найдена увеличивающая цепь, перед выполнением следующего шага окраска снимается со всех дуг и со всех вершин, кроме истока
, по которой поток может быть увеличен на 1. Напомним, что в соответствии с используемым методом из [34] перед началом его работы значения потоков на всех дугах сети полагаются равными 0. Поскольку на 6-м шаге найдена увеличивающая цепь, перед выполнением следующего шага окраска снимается со всех дуг и со всех вершин, кроме истока  . На 8-м шаге из окрашенных дуг вновь может быть построена увеличивающая цепь
. На 8-м шаге из окрашенных дуг вновь может быть построена увеличивающая цепь  , по которой поток может быть увеличен на 1. Наконец, на 9-м шаге из окрашенных дуг строится увеличивающая цепь
, по которой поток может быть увеличен на 1. Наконец, на 9-м шаге из окрашенных дуг строится увеличивающая цепь 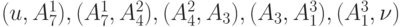 , по которой поток также может быть увеличен на 1.
, по которой поток также может быть увеличен на 1.
На этом алгоритм решения задачи о потоке минимальной стоимости заканчивает работу, поскольку в сети получен максимальный поток величины 3. Полученным выше трем увеличивающим цепям соответствуют три следующих пути в исходной сети, по которым должно производиться восстановление сигнала на первичных входах сети:
-
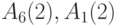 ;
; -
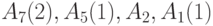 ;
; -
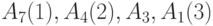 .
.
Время восстановления сигналов по этим путям на первичных входах сети соответственно равно 6, 8 и 8 тактам времени. Следовательно, общее минимальное время восстановления входного вектора равно 22 тактам. Целью рассмотрения этого простого примера является иллюстрация методики построения порожденной сети по исходной, а также возможности существования в сети альтернативных путей для восстановления сигнала на внешнем входе. Так, для входа 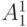 сети существует еще один путь восстановления сигнала на нем -
сети существует еще один путь восстановления сигнала на нем - 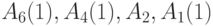 , кроме приведенного выше пути. Однако время восстановления сигнала по этому пути равно 9 тактам. Аналогичная ситуация имеет место и для внешнего входа
, кроме приведенного выше пути. Однако время восстановления сигнала по этому пути равно 9 тактам. Аналогичная ситуация имеет место и для внешнего входа 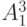 : существует еще один путь -
: существует еще один путь - 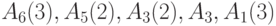 - с временем восстановления 9 тактов.
- с временем восстановления 9 тактов.
В заключение заметим, что предложенный метод решения рассмотренной задачи может быть распространен и для сетей из ЛА БПИ, которые являются избыточными по входам. Для этого необходимо идентифицировать избыточные выходы в каждом автомате-компоненте и исключить их из дальнейшего рассмотрения. Такую идентификацию можно осуществить путем преобразования матрицы системы уравнений (17.2) по методу Гаусса решения систем линейных уравнений. Если в процессе преобразования некоторые строки матрицы вырождаются в нулевые, то это и является признаком линейной зависимости соответствующего выхода от других, т. е. его избыточности.
Вопросы и упражнения
- Сформулируйте правила построения корректной сети из базисных ЛА.
- Дайте определение покрывающего множества путей сети.
- Приведите постановку задачи минимизации времени восстановления неизвестных входных сигналов в сети из линейных автоматов без потери информации.
- Какова основная идея метода решения задачи, сформулированной в пункте 3 ?
- Опишите идею способа сведения исследуемой задачи к задаче о потоке минимальной стоимости из теории потоков.
- Что такое порожденная сеть и каковы правила ее построения?
- Опишите три этапа алгоритма решения задачи о минимизации времени восстановления неизвестных входных сигналов по наблюдаемым выходам.