Минимизация времени восстановления неизвестных входных сигналов в сети из автоматов без потери информации
Задача, упомянутая в заголовке лекции, возникает, в частности, при организации функционального контроля ЦУ. Как было сказано ранее, для этой цели могут быть использованы СВК, позволяющие восстанавливать неизвестные входные сигналы ЦУ по его выходной реакции, с последующим сравнением их с реальными сигналами, поступившими на вход ЦУ. Рассогласование этих сигналов свидетельствует о неправильном функционировании ЦУ и может быть зафиксировано в момент первого его проявления. Последнее обстоятельство очень важно, поскольку позволяет не допускать распространения появившейся ошибки.
Восстановление неизвестной входной последовательности по известному начальному состоянию автомата и наблюдаемой реакции в случае ЛА сводится, как известно [19], к решению системы линейных уравнений. Сложность решения такой системы, определяемая, например, необходимым для этого временем, зависит от размерности, а также от сложности вычисления выражений, определяющих значения правых частей системы, которая, в свою очередь, зависит от структуры схемы ЛА. Сеть, построенную из  штук ЛА БПИ над полем
штук ЛА БПИ над полем 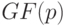 , можно описать моделью одного ЛА БПИ, размерность которого равна
, можно описать моделью одного ЛА БПИ, размерность которого равна  , где
, где  - размерности входящих в состав сети автоматов-компонентов. Тогда восстановление неизвестных входных сигналов сети связано с решением системы линейных уравнений с
- размерности входящих в состав сети автоматов-компонентов. Тогда восстановление неизвестных входных сигналов сети связано с решением системы линейных уравнений с  неизвестными, где
неизвестными, где  - число входов сети. Вместе с тем упомянутое восстановление, поскольку структура сети известна, может быть сведено к решению
- число входов сети. Вместе с тем упомянутое восстановление, поскольку структура сети известна, может быть сведено к решению  систем линейных уравнений меньшей размерности, каждая из которых соответствует отдельному компоненту сети. Понятно, что последний способ восстановления может оказаться более эффектным, т. е. требовать существенно меньшего времени на реализацию. В случае, когда время является критическим параметром, СВК, построенная вторым способом, будет предпочтительнее СВК, построенной первым способом, поскольку время решения систем уравнений определяет быстродействие СВК.
систем линейных уравнений меньшей размерности, каждая из которых соответствует отдельному компоненту сети. Понятно, что последний способ восстановления может оказаться более эффектным, т. е. требовать существенно меньшего времени на реализацию. В случае, когда время является критическим параметром, СВК, построенная вторым способом, будет предпочтительнее СВК, построенной первым способом, поскольку время решения систем уравнений определяет быстродействие СВК.
Отметим, что СВК, синтезируемая вторым способом, определяется неоднозначно, поскольку восстановление одного и того же компонента входного сигнала сети может быть осуществлено по различным путям рассматриваемой сети и потому время восстановления этого компонента может быть различным в зависимости от выбранного пути. В связи с изложенным возникает задача минимизации общего времени восстановления входных сигналов сети из ЛА БПИ, которая рассматривается в этой лекции.
Пусть задано некоторое конечное множество ЛА 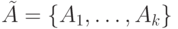 , которое далее именуется базисом, а каждый элемент этого множества - базисным. Предполагается, что сеть содержит в качестве компонентов ЛА
, которое далее именуется базисом, а каждый элемент этого множества - базисным. Предполагается, что сеть содержит в качестве компонентов ЛА  . Помимо элементов сеть содержит входные и выходные полюсы. Из базисных элементов сети будут строиться по определенным правилам. Опишем эти правила, используя индукцию:
. Помимо элементов сеть содержит входные и выходные полюсы. Из базисных элементов сети будут строиться по определенным правилам. Опишем эти правила, используя индукцию:
- совокупность первичных входных полюсов, соответствующих различным переменным сети, есть сеть, и все эти полюсы являются ее вершинами;
- результат присоединения к вершинам сети входов (необязательно всех) некоторого базисного элемента есть сеть; вершинами новой сети являются все вершины исходной сети, незадействованные (если таковые имеются) входы, а также выходы присоединенного элемента;
- результат присоединения к вершинам сети входов (кроме внешних полюсов) и/или выходов некоторого базисного элемента есть снова сеть, вершинами которой являются все вершины сети, полученной на предыдущем этапе, незадействованные (если таковые имеются) входы, а также все выходы присоединенного элемента.
В сети выделяется некоторое подмножество вершин, именуемых внешними выходными полюсами.
Сеть, в которой отсутствуют незадействованные входы используемых в ее составе базисных элементов, назовем корректной. Далее рассматриваются только корректные сети.
Из описанных правил построения сети следует, что с содержательной точки зрения корректной сети соответствует "правильная" электрическая схема, содержащая в общем случае параллельно и/или последовательно соединенные компоненты, а также линии обратной связи.
Далее предполагается, что у каждого компонента сети отсутствуют соединения его выходов с его же входами, т. е. отсутствуют петли обратной связи. Это предположение не является ограничительным, поскольку в случае существования у компонента такого вида соединения его можно отнести к его внутренней структуре, а сам компонент рассматривать как "черный ящик", содержащий только те входы и выходы, которые связывают его с другими базисными элементами сети или внешними входами (выходами).
Выходной канал  ЛА назовем избыточным, если в любой момент времени
ЛА назовем избыточным, если в любой момент времени  значение сигнала
значение сигнала  на нем есть линейная комбинация сигналов на других выходных каналах этого же ЛА.
на нем есть линейная комбинация сигналов на других выходных каналах этого же ЛА.
Назовем ЛА неизбыточным по выходам, если в нем отсутствуют избыточные выходные каналы.
Напомним, что любой ЛА над полем 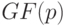 задается системами уравнений состояний и выходов соответственно:
задается системами уравнений состояний и выходов соответственно:
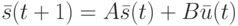 |
( 17.1) |
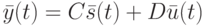 |
( 17.2) |
Выражение (17.2) можно интерпретировать как систему линейных уравнений относительно 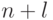 неизвестных
неизвестных 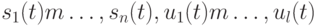 , где
, где  - размерность ЛА,
- размерность ЛА,  - число его входных каналов.
- число его входных каналов.
Лемма 17.1. Для того чтобы ЛА был неизбыточным по выходам, необходимо и достаточно, чтобы число его выходных каналов было равно рангу матрицы системы (17.2).
Доказательство. Пусть ранг системы (17.2) равен  , где
, где 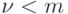 (где
(где  - число выходных каналов ЛА). Известно из [33], что это условие является необходимым и достаточным для того, чтобы
- число выходных каналов ЛА). Известно из [33], что это условие является необходимым и достаточным для того, чтобы  уравнений упомянутой системы были линейными комбинациями остальных уравнений. Применительно к ЛА этот факт означает, что
уравнений упомянутой системы были линейными комбинациями остальных уравнений. Применительно к ЛА этот факт означает, что 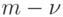 его выходных каналов являются избыточными. Отсюда и вытекает справедливость леммы.
его выходных каналов являются избыточными. Отсюда и вытекает справедливость леммы.
Лемма 17.2. Для того чтобы ЛА был БПИ и неизбыточным по выходам, необходимо и достаточно, чтобы выполнялись следующие условия:
- число входных каналов равно числу выходных (
 );
); - ранг матрицы
 равен
равен  .
.
Доказательств. В [19] доказано, что ЛА есть ЛА БПИ тогда и только тогда, когда ранг матрицы  равен
равен  , т. е. второе условие леммы выполняется. Для ЛА БПИ начальное состояние
, т. е. второе условие леммы выполняется. Для ЛА БПИ начальное состояние  считается известным. Зная
считается известным. Зная  и реакцию
и реакцию  , решив систему (17.2) относительно переменных
, решив систему (17.2) относительно переменных 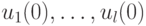 , получим неизвестный входной символ
, получим неизвестный входной символ  . Зная
. Зная  , с помощью формулы (17.2) вычислим состояние
, с помощью формулы (17.2) вычислим состояние 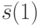 . Аналогичным образом можно определить состояние
. Аналогичным образом можно определить состояние  для
для 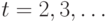 Тогда система (17.2) для ЛА БПИ вырождается в систему
Тогда система (17.2) для ЛА БПИ вырождается в систему
 |
( 17.3) |
относительно неизвестных 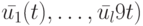 с матрицей
с матрицей  . Отсюда на основании леммы 17.1 можно утверждать, что неизбыточность по выходам ЛА БПИ имеет место тогда и только тогда, когда число
. Отсюда на основании леммы 17.1 можно утверждать, что неизбыточность по выходам ЛА БПИ имеет место тогда и только тогда, когда число  его выходных каналов будет равно рангу матрицы
его выходных каналов будет равно рангу матрицы  , т. е. числу
, т. е. числу  .
.
Далее рассматриваются сети, построенные только из ЛА БПИ, неизбыточных по выходам. Очевидно, что любая сеть из ЛА БПИ такого типа представляет собой ЛА БПИ, но необязательно неизбыточный по выходам.
Перейдем теперь к постановке задачи. Рассмотрим сеть из ЛА БПИ, неизбыточных по выходам, в которой вершинами являются автоматы-компоненты и все ее внешние входы и внешние выходы. Каждому каналу (соединению) сети, связывающему две его вершины, поставим в соответствие целое неотрицательное число, называемое весовым коэффициентом. Значение весового коэффициента определяется типом канала. Если канал связывает выход некоторого автомата-компонента со входом другого автомата-компонента или некоторый вход сети со входом автомата-компонента, то соответствующий этому каналу весовой коэффициент положим равным числу тактов времени, необходимому для вычисления значения сигнала на упомянутом входе путем решения соответствующей системы линейных уравнений вида (17.3). В случае, когда канал связывает выход некоторого автомата-компонента с одним из внешних выходов сети, соответствующий ему весовой коэффициент положим равным нулю. Последнее объясняется тем, что значение сигнала на выходе сети может наблюдаться непосредственно, т. е. не требует никаких вычислений.
Если в сети существует путь от внешнего входа  к внешнему выходу
к внешнему выходу  , то будем считать временем восстановления значения сигнала на входе
, то будем считать временем восстановления значения сигнала на входе  вдоль упомянутого пути сумму весовых коэффициентов каналов, входящих в путь. Множество путей в сети, связывающее каждый внешний вход сети с одним из ее внешних выходов, назовем покрывающим множеством. Очевидно, что знание покрывающего множества путей сети позволяет восстановить неизвестный входной вектор сети по наблюдаемой реакции сети и ее известному начальному состоянию. Назовем суммарные временные затраты на восстановление всех составляющих входного вектора сети вдоль всех путей покрывающего множества временем восстановления входного вектора.
вдоль упомянутого пути сумму весовых коэффициентов каналов, входящих в путь. Множество путей в сети, связывающее каждый внешний вход сети с одним из ее внешних выходов, назовем покрывающим множеством. Очевидно, что знание покрывающего множества путей сети позволяет восстановить неизвестный входной вектор сети по наблюдаемой реакции сети и ее известному начальному состоянию. Назовем суммарные временные затраты на восстановление всех составляющих входного вектора сети вдоль всех путей покрывающего множества временем восстановления входного вектора.
Рассматриваемая здесь задача заключается в построении для заданной сети из ЛА БПИ покрывающего множества путей с минимальным временем восстановления входного вектора.
Перейдем к описанию метода решения сформулированной задачи. Идея предлагаемого метода состоит в редукции ее к классической задаче о потоке минимальной стоимости в сети [3] порожденной исходной сетью. Обозначим исходную сеть, построенную из ЛА БПИ, неизбыточных по выходам, через  , а порожденную ею сеть - через
, а порожденную ею сеть - через 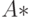 .
.
Опишем правила, по которым из исходной сети строится порожденная ею сеть. Условимся, что все входные и выходные каналы каждого автомата-компонента сети пронумерованы числами от 1 до  , если он имеет
, если он имеет  входов
входов
Каждому автомату-компоненту  сети
сети  , имеющему
, имеющему  входов (выходов), в порожденной сети
входов (выходов), в порожденной сети 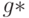 соответствует
соответствует  вершин
вершин 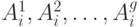 . Если в исходной сети
. Если в исходной сети  -й выход автомата
-й выход автомата  соединен каналом связи с
соединен каналом связи с  -м входом автомата
-м входом автомата 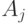 той же сети, то в порожденной сети соединим вершину
той же сети, то в порожденной сети соединим вершину  с вершиной
с вершиной 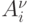 дугой, заходящей в
дугой, заходящей в 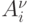 (направление этой дуги противоположно направлению распространения сигнала в реальной сети по этому каналу). Далее, если в исходной сети ее внешний вход (внешний выход)
(направление этой дуги противоположно направлению распространения сигнала в реальной сети по этому каналу). Далее, если в исходной сети ее внешний вход (внешний выход)  соединен с
соединен с  -м входом (выходом) автомата-компонента
-м входом (выходом) автомата-компонента  , то в порожденной сети соединим вершину
, то в порожденной сети соединим вершину  с вершиной
с вершиной 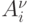 дугой, заходящей в вершину
дугой, заходящей в вершину  (в вершину
(в вершину 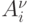 ). Направление упомянутых дуг также противоположно направлению распространения сигнала по соответствующим каналам в реальной сети. К множеству вершин порожденной сети, описанному выше, добавим еще две вершины
). Направление упомянутых дуг также противоположно направлению распространения сигнала по соответствующим каналам в реальной сети. К множеству вершин порожденной сети, описанному выше, добавим еще две вершины  и
и  . Вершину
. Вершину  соединим дугами со всеми вершинами порожденной сети, соответствующими внешним выходам исходной сети, заходящими в них. Аналогично, все вершины порожденной сети, соответствующие внешним входам исходной сети, соединим дугами с вершиной
соединим дугами со всеми вершинами порожденной сети, соответствующими внешним выходам исходной сети, заходящими в них. Аналогично, все вершины порожденной сети, соответствующие внешним входам исходной сети, соединим дугами с вершиной 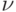 , заходящими в нее.
, заходящими в нее.
Опишем теперь правила назначения пропускных способностей дугам порожденной сети:
- пропускную способность каждой дуги вида
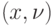 порожденной сети положим равной 1;
порожденной сети положим равной 1; - пропускные способности всех остальных дуг порожденной сети положим равными бесконечности.
Теперь остается описать правила назначения каждой дуге порожденной сети соответствующего весового коэффициента, который играет роль стоимости прохождения единицы потока в классической задаче о потоке минимальной стоимости.
Каждой дуге, исходящей из вершины  порожденной сети, назначим весовой коэффициент, равный 0.
порожденной сети, назначим весовой коэффициент, равный 0.
Пусть автомат-компонент  сети имеет
сети имеет  входов (выходов). Как уже упоминалось выше, восстановление значений сигналов на его входах по наблюдаемой реакции при известном начальном состоянии требует решения соответствующей системы линейных уравнений. Пусть время решения такой системы равно
входов (выходов). Как уже упоминалось выше, восстановление значений сигналов на его входах по наблюдаемой реакции при известном начальном состоянии требует решения соответствующей системы линейных уравнений. Пусть время решения такой системы равно  единицам времени, если в качестве единицы принять временной такт. Каждому автомату-компоненту
единицам времени, если в качестве единицы принять временной такт. Каждому автомату-компоненту  исходной сети с
исходной сети с  входами соответствует
входами соответствует  вершин
вершин 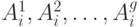 порожденной сети. Положим значения весовых коэффициентов дуг, исходящих из упомянутых вершин, равными величине
порожденной сети. Положим значения весовых коэффициентов дуг, исходящих из упомянутых вершин, равными величине  .
.
Таким образом, по исходной сети  нами построена порожденная сеть
нами построена порожденная сеть 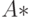 с одним истоком
с одним истоком  и одним стоком
и одним стоком  , где каждой дуге соответствует пара чисел, первое из которых есть весовой коэффициент, а второе - пропускная способность.
, где каждой дуге соответствует пара чисел, первое из которых есть весовой коэффициент, а второе - пропускная способность.
Отметим, что используемые ниже, но не определяемые здесь понятия и терминология из теории потоков в сетях трактуются так, как они определены в [34].
Установим два свойства порожденной сети, сформулированные в виде лемм.
