НОУ ИНТУИТ | Введение в Octave. Лекция 7: Нелинейные уравнения и системы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 587 / 65 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

7.4 Решение нелинейных уравнений и систем в символьных переменных

Напомним, что для работы с символьными переменными в Octave должен быть подключён специальный пакет расширений octave-symbolic. Процедура установки пакетов расширений описана в первой главе. Техника работы с символьными переменными описана в п. 2.7 второй главы.

Для решения системы нелинейных уравнений или одного нелинейного уравнения можно воспользоваться функцией symfsolve .

Пример 7.21. Решить уравнение 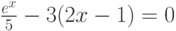$\frac{e^x}{5}-3(2x-1)=0$ .

Рис. 7.9. Графическое решение примера 7.21

Команды, с помощью которых выполнено графическое (рис. 7.9) и аналитическое решение представлены в листинге 7.24.

	
clear all; clf; cla;
symbols
x=sym("x");
y=Exp(x)/5-3-(2-x-1);
L=ezplot(’exp(x)/5-3*(2*x-1)’);
set(L, ’LineWidth’, 2, ’Color’, ’k’)
set(gca, ’xlim’, [-2,6]); set(gca, ’ylim’, [-20, 50]);
set(gca, ’xtick’,[-2:0.5:6]); set(gca, ’ytick’, [-20:10:50]);
grid on; xlabel(’x’); ylabel(’y’);
>>> q1 = symfsolve(y, 0)
>>> q2 = symfsolve(y, 4)
q1 = 0.55825
q2 = 4.8777

Листинг 7.24. Решение системы с помощью symfsolve (пример 7.21).

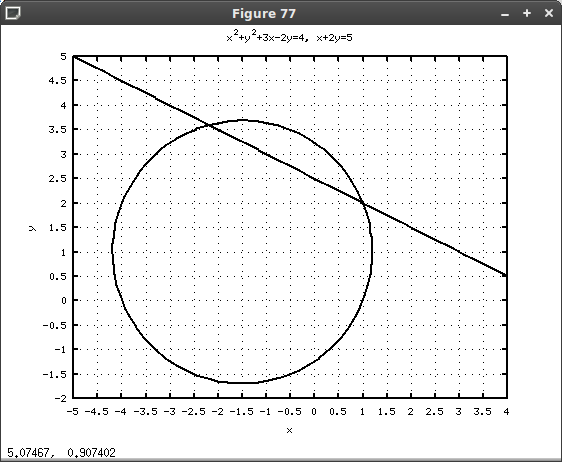
Пример 7.22. Решить систему:

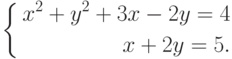
$\left\{\begin{aligned}x^2+y^2+3x-2y=4\\ x+2y=5.\end{aligned}$

Рис. 7.10. Графическое решение примера 7.22

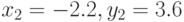Решение системы (листинг 7.25) показало, что она имеет два корня x_1=1,y_1=2 и x_2=-2.2,y_2=3.6 , что соответствует графическому решению (рис. 7.10).

	
clear all; clf; cla;
symbols
x=sym("x");
y=sym("y");
L1=ezplot(’x^2+y^2+3*x-2*y-4’); set(L1, ’LineWidth’, 2, ’Color’, ’k
	’)
hold on
L2=ezplot(’x+2*y-5’); set(L2, ’LineWidth’, 2, ’Color’, ’k’)
set(gca, ’xlim’, [-5, 4]); set(gca, ’ylim’, [-2, 5]);
set(gca, ’xtick’, [-5:0.5:4]); set(gca, ’ytick’, [-2:0.5:5]);
grid on; xlabel(’x’); ylabel(’y’);
title(’x^2+y^2+3x-2y=4, x+2y=5’)
f1=x^2+y^2+3-x-2-y-4;
f2=x+2-y-5;
>>> q1 = symfsolve(f1, f2, {x==0,y==1})
>>> q2 = symfsolve(f1, f2, {x==-1,y==3})
q1 = 1.0000  2.0000
q2 = -2.2000  3.6000

Листинг 7.25. Решение системы с помощью symfsolve (пример 7.22).

Дальше >>

Авторизоваться

Введение в Octave

Нелинейные уравнения и системы

7.4 Решение нелинейных уравнений и систем в символьных переменных

Вопросы и ответы