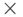|
Возможна ли разработка приложения на Octave с GUI? |
Построение графиков
4.1 Построение двумерных графиков
Двумерным будем считать такой график, в котором положение точки определяется двумя величинами. Двумерные графики наиболее часто строят в декартовой и полярной системах координат.
4.1.1 Построение графиков в декартовой системе координат
Декартова, или прямоугольная система координат задаётся двумя перпендикулярными прямыми, называемыми осями координат. Горизонтальная прямая  — ось абсцисс, а вертикальная
— ось абсцисс, а вертикальная  — ось ординат. Точку пересечения осей называют началом координат. Четыре угла, образованные осями координат, носят название координатных углов. Положение точки в прямоугольной системе координат определяется значением двух величин, называемых координатами точки. Если точка имеет координаты
— ось ординат. Точку пересечения осей называют началом координат. Четыре угла, образованные осями координат, носят название координатных углов. Положение точки в прямоугольной системе координат определяется значением двух величин, называемых координатами точки. Если точка имеет координаты  и
и  , то
, то  — абсцисса точки,
— абсцисса точки,  — ордината. Уравнение, связывающее координаты
— ордината. Уравнение, связывающее координаты  и
и  является (называется) уравнением линии, если координаты любой точки этой линии удовлетворяют ему.
является (называется) уравнением линии, если координаты любой точки этой линии удовлетворяют ему.
Величина y называется функцией переменной величины  , если каждому из тех значений, которые может принимать
, если каждому из тех значений, которые может принимать  , соответствует одно или несколько определённых значений
, соответствует одно или несколько определённых значений  . При этом переменная величина
. При этом переменная величина  называется аргументом функции
называется аргументом функции  . Говорят также, что величина
. Говорят также, что величина  зависит от величины
зависит от величины  . Функция считается заданной, если для каждого значения аргумента существует соответствующее значение функции. Чаще всего используют следующие способы задания функций:
. Функция считается заданной, если для каждого значения аргумента существует соответствующее значение функции. Чаще всего используют следующие способы задания функций:
- табличный — числовые значения функции уже заданы и занесены в таблицу; недостаток заключается в том, что таблица может не содержать все нужные значения функции;
- графический — значения функции заданы при помощи линии (графика), у которой абсциссы изображают значения аргумента, а ординаты — соответствующие значения функции;
- аналитический — функция задаётся одной или несколькими формулами (уравнениями); при этом, если зависимость между
 и
и  выражена уравнением, разрешённым относительно
выражена уравнением, разрешённым относительно  , то говорят о явно заданной функции, в противном случае функция считается неявной.
, то говорят о явно заданной функции, в противном случае функция считается неявной.
Совокупность всех значений, которые может принимать в условиях поставленной задачи аргумент  функции
функции  , называется областью определения этой функции. Совокупность значений
, называется областью определения этой функции. Совокупность значений  , которые принимает функция
, которые принимает функция  , называется множеством значений функции.
, называется множеством значений функции.
Далее будем рассматривать построение графиков в прямоугольной системе координат на конкретных примерах.
Пример 4.1. Построить график функции  на интервале [-10; 10].
на интервале [-10; 10].
Для того, чтобы построить график функции  необходимо сформировать два массива
необходимо сформировать два массива  и
и  одинаковой размерности, а затем обратиться к функции
одинаковой размерности, а затем обратиться к функции 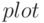 .
.
Решение этой задачи представлено в листинге 4.1.
x = -10:0.1:10; % Формирование массива x. y=sin(x)+sin (3*x)/3+ sin (5*x )/5; % Формирование массива y. plot(x, y) % Построение графика функции.Листинг 4.1. Построение графика (пример 4.1).
В результате обращения к функции 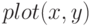 будет создано окно с именем Figure 1, в котором будет построен график функции
будет создано окно с именем Figure 1, в котором будет построен график функции  .
.
График формируется путём соединения соседних точек прямыми линиями. Чем больше будет интервал между соседними точками (чем меньше будет точек), тем больше будет заметно, что график представляет из себя ломанную.
Если повторно обратиться к функции 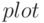 , то в этом же окне будет стёрт первый график и нарисован второй. Для построения нескольких графиков в одной системе координат можно поступить одним из следующих способов:
, то в этом же окне будет стёрт первый график и нарисован второй. Для построения нескольких графиков в одной системе координат можно поступить одним из следующих способов:
- Обратиться к функции plot следующим образом
 — массивы абсцисс и ординат первого графика,
— массивы абсцисс и ординат первого графика,  — массивы абсцисс и ординат второго графика,
— массивы абсцисс и ординат второго графика, 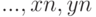 — массивы абсцисс и ординат n-ого графика.
— массивы абсцисс и ординат n-ого графика. - Каждый график изображать с помощью функции
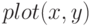 , но перед обращением к функциям
, но перед обращением к функциям 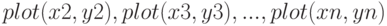 вызвать команду hold
on1Команда
вызвать команду hold
on1Команда 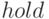 работает в режиме переключателя:
работает в режиме переключателя: 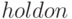 — блокирует режим очистки экрана,
— блокирует режим очистки экрана, 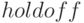 — включает режим очистки экрана., которая блокирует режим очистки окна.
— включает режим очистки экрана., которая блокирует режим очистки окна.
Рассмотрим построение нескольких графиков этими способами на примере решения следующей задачи.
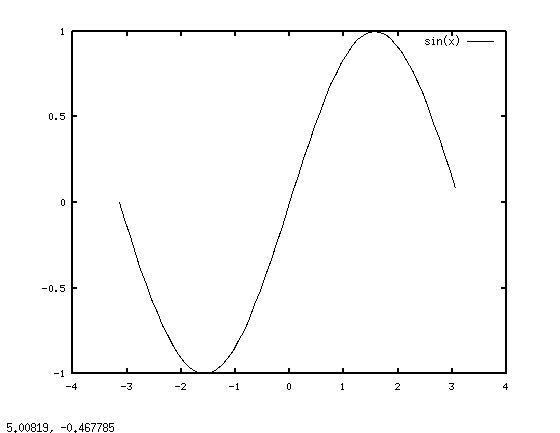
На рис. 4.2. изображены графики функций: 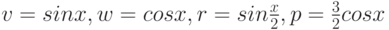
Пример 4.2. Построить графики функций 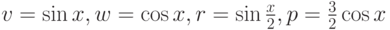 на интервале
на интервале ![[-4\pi; 4\pi]](/sites/default/files/tex_cache/5ce2d5d799a3d3f3793a1f80b2f5e68c.png) .
.
Построение графиков функций первым и вторым способом представлено в листинге 4.2. Получившиеся графики функций представлены на рис. 4.2.
% Способ первый x=-4*pi:0.1:4*pi; v=sin(x);w=cos(x); r=sin(x)/2; p=1.5*cos(x); plot(x, v, x, w, x, r, x, p); % Способ второй x=-4*pi:0.1:4*pi; v=sin(x); plot(x, v); hold on; v=cos(x); plot(x, v); v=sin(x)/2; plot(x, v); v=1.5*cos(x); plot(x, v);Листинг 4.2. Два способа построения графика (пример 4.2).
Обратите внимание, что при построении графиков первым способом Octave> автоматически изменяет цвета изображаемых в одной системе координат графиков. Однако управлять цветом и видом каждого из изображаемых графиков может и пользователь, для чего необходимо воспользоваться полной формой функции  , где
, где 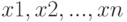 — массивы абсцисс графиков;
— массивы абсцисс графиков;  — массивы ординат графиков;
— массивы ординат графиков;
| Символ | Цвет линии |
| y | жёлтый |
| m | розовый |
| c | голубой |
| r | красный |
| g | зелёный |
| d | синий |
| w | белый |
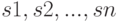 — строка форматов, определяющая параметры линии и при необходимости, позволяющая вывести легенду.
— строка форматов, определяющая параметры линии и при необходимости, позволяющая вывести легенду.
В строке могут участвовать символы, отвечающие за тип линии, маркер, его размер, цвет линии и вывод легенды. Попробуем разобраться с этими символами. За сплошную линию отвечает символ "-". За маркеры отвечают следующие символы (см. табл. 4.1).
Цвет линии определяется буквой латинского алфавита (см. табл.4.2), можно использовать и цифры, но на взгляд авторов использование букв более логично (их легче запомнить по английским названиям цветов).
При определении строки, отвечающей за вывод линии, следует учитывать следующее:
- не важен порядок символа цвета и символа маркера;
- если присутствует символ "-", то линия всегда будет сплошная, при этом, если присутствует символ маркера, то все изображаемые точки ещё будут помечаться маркером, если символа маркера нет, то соседние точки просто будут соединяться линиями;
- если символ маркера "-" отсутствует, то линия может быть, как сплошная, так и точечная; это зависит от наличия символа маркера, если символа маркера нет, то будет сплошная линия, иначе — точечная.
Если необходима легенда для графика, то её следует включить в строку форматов, заключённую в символы ";". Например, команда 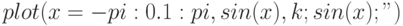 выведет на экран график функции
выведет на экран график функции  чёрного цвета на интервале
чёрного цвета на интервале ![[-\pi; \pi]](/sites/default/files/tex_cache/59c9cb397e96086b5e4a2e4804d7af92.png) c легендой
c легендой 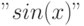 (см. рис. 4.3)
(см. рис. 4.3)
Пользователь может управлять и величиной маркера, для этого после строки форматов следует указать имя параметра  (размер маркера) и через запятую величину — целое число, определяющее размер маркера на графике. Например, команда
(размер маркера) и через запятую величину — целое число, определяющее размер маркера на графике. Например, команда  , 4); выведет на экран график, представленный на рис. 4.4.
, 4); выведет на экран график, представленный на рис. 4.4.
увеличить изображение
Рис. 4.4. Результаты работы функции plot(x = -pi:0.1:pi, sin(x), " -ok; sin(x); ", "markersize", 4);
Для того, чтобы чтобы вывести график в новом окне, перед функцией plot, следует вызвать функцию 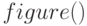 .
.
Внимание! При работе с графиками в Octave необходимо понимать следующее: щелчок по кнопке закрытия окна с графиками приводит не к уничтожению (закрытию) окна, а к его скрытию. При повторном вызове команды рисования графиков происходит восстановление окна, в котором и изображаются графики. Корректное закрытие графического окна можно осуществить в Octave только программно.
Графическое окно создаётся функцией 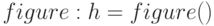 ;
;
Здесь  — переменная, в которой будет храниться дескриптор (номер) окна. Для дальнейших операций с окном надо будет использовать именно переменную, в которой хранится дескриптор.
— переменная, в которой будет храниться дескриптор (номер) окна. Для дальнейших операций с окном надо будет использовать именно переменную, в которой хранится дескриптор.
Уничтожение (закрытие) окна осуществляется с помощью функции  , где
, где  — имя дескриптора закрываемого окна.
— имя дескриптора закрываемого окна.
В Octave есть функция  , которая приостанавливает выполнение программы на
, которая приостанавливает выполнение программы на  секунд. Её логично вставлять перед функцией закрытия окна.
секунд. Её логично вставлять перед функцией закрытия окна.
Octave представляет дополнительные возможности для оформления графиков:
- команда
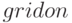 наносит сетку на график,
наносит сетку на график, 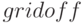 убирает сетку с графика;
убирает сетку с графика; - функция
![axis[xmin, xmax, ymin, ymax]](/sites/default/files/tex_cache/d00388c80ddf97d58a1350f6159b5ce0.png) выводит только часть графика, определяемую прямоугольной областью
выводит только часть графика, определяемую прямоугольной областью  ;
; - функция
 предназначена для вывода заголовка графика;
предназначена для вывода заголовка графика; - функции
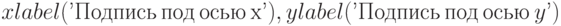 служат для подписей осей
служат для подписей осей  и
и  соответственно;
соответственно; - функция
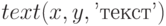 выводит текст левее точки с координатами
выводит текст левее точки с координатами  ;
; - функция
 выводит легенды для каждого из графиков, параметр
выводит легенды для каждого из графиков, параметр  определяет месторасположение легенды в графическом окне: 1 — в правом верхнем углу графика (значение по умолчанию); 2 — в левом верхнем углу графика; 3 — в левом нижнем углу графика; 4 — в правом нижнем углу графика.
определяет месторасположение легенды в графическом окне: 1 — в правом верхнем углу графика (значение по умолчанию); 2 — в левом верхнем углу графика; 3 — в левом нижнем углу графика; 4 — в правом нижнем углу графика.
При выводе текста с помощью функций  можно выводить греческие
буквы2Для вывода греческих букв и кириллицы в вашей операционной системе должны быть установлены соответствующие шрифты.
(см. табл. 4.3), использовать символы верхнего и нижнего индекса. Для вывода текста в верхнем индексе используется символ "^", в нижнем — символ "_". Например, для вывода
можно выводить греческие
буквы2Для вывода греческих букв и кириллицы в вашей операционной системе должны быть установлены соответствующие шрифты.
(см. табл. 4.3), использовать символы верхнего и нижнего индекса. Для вывода текста в верхнем индексе используется символ "^", в нижнем — символ "_". Например, для вывода 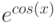 необходимо будет ввести текст e^{cos(x)}, а для вывода
необходимо будет ввести текст e^{cos(x)}, а для вывода 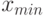 — текст x_{min}. При работе с текстом можно также использовать синтаксис
— текст x_{min}. При работе с текстом можно также использовать синтаксис  .
.
| Команда | Символ | Команда | Символ |
| \alpha |  |
\upsilon | 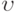 |
| \beta |  |
\phi |  |
| \gamma |  |
\chi | 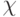 |
| \delta |  |
\psi |  |
| \epsilon | 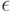 |
\omega |  |
| \zeta |  |
\Gamma |  |
| \eta |  |
\Delta |  |
| \theta |  |
\Theta |  |
| \iota | 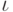 |
\Lambda |  |
| \kappa | 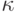 |
\Xi |  |
| \lambda |  |
\Pi |  |
| \mu |  |
\Sigma |  |
| \nu |  |
\Upsilon | 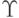 |
| \xi |  |
\Phi |  |
| \pi |  |
\Psi |  |
| \rho |  |
\Omega |  |
| \sigma |  |
\forall | 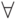 |
| \varsigma | 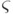 |
\exists |  |
| \tau |  |
\approx |  |
| \int | 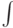 |
\in | 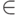 |
| \wedge |  |
\sim | 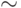 |
| \vee |  |
\leq |  |
| \pm |  |
\leftrightarrow | 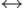 |
| \geq |  |
\leftarrow |  |
| \infty |  |
\uparrow | 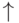 |
| \partial | 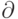 |
\rightarrow |  |
| \neq | 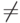 |
\downarrow | 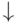 |
| \nabla |  |
\circ |  |
После описания основных возможностей по оформлению графиков рассмотрим ещё несколько примеров построения графиков.
Пример 4.3. Последовательно вывести в графическое окно графики функций 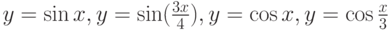 с задержкой 5 секунд.
с задержкой 5 секунд.
Текст решения задачи с комментариями приведён в листинге 4.3.
okno1=figure( ); % Создаём графическое окно c дескриптором okno1. x=-6*pi( ):pi( )/50:6*pi( ); % Определяем аргумент на интервалеЛистинг 4.3. Построение графиков (пример 4.3).y=sin(x); % Вычисляем значение функции sin(x). plot(x, y, ’k’); % Выводим график функции sin(x) чёрного цвета. grid on; % Выводим линии сетки. title(’Plot y=sin(x)’ ); % Выводим заголовок графика. pause(5); % Приостанавливаем выполнение программы на 5 секунд. y=sin(0.75*x); plot(x, y, ’b’); % Выводим график функции sin(0.75x) голубого цвета. grid on; % Выводим линии сетки. title(’Plot y=sin(0.75x)’);% Выводим заголовок графика. pause(5); % Приостанавливаем выполнение программы на 5 секунд. y=cos(x); plot(x, y, ’r’); % Выводим график функции cos(x) красного цвета. grid on; % Выводим линии сетки. title(’Plot y=cos(x)’); % Выводим заголовок графика. pause(5); % Приостанавливаем выполнение программы на 5 секунд. y=cos(x /3); plot(x, y, ’g’); % Выводим график функции cos(x/3) зелёного цвета. grid on; % Выводим линии сетки. title(’Plot y=cos(x/3)’); % Выводим заголовок графика. pause(5); % Приостанавливаем выполнение программы на 5 секунд. delete(okno1); % Закрываем окно с дескриптором okno1.
При запуске программы будет создано графическое окно, в котором будет выведен график функции  чёрного цвета с линиями сетки и заголовком. Это окно будет находиться на экране в течении 5 секунд, после чего очистится. Будет выведен график функции
чёрного цвета с линиями сетки и заголовком. Это окно будет находиться на экране в течении 5 секунд, после чего очистится. Будет выведен график функции  голубого цвета с линиями сетки и заголовком, которое будет на экране в течении 5 секунд. Далее аналогично будут с задержками 5 секунд выведены графики функций
голубого цвета с линиями сетки и заголовком, которое будет на экране в течении 5 секунд. Далее аналогично будут с задержками 5 секунд выведены графики функций  и
и 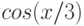 . После этого окно автоматически закроется. Для понимания механизма работы с графическими окнами в Octave, авторы рекомендуют читателю при выводе графика
. После этого окно автоматически закроется. Для понимания механизма работы с графическими окнами в Octave, авторы рекомендуют читателю при выводе графика  попытаться закрыть окно и посмотреть, что из этого получится.
попытаться закрыть окно и посмотреть, что из этого получится.
Пример 4.4. Построить графики функций 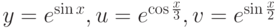 на интервале
на интервале ![[-3\pi; 3\pi]](/sites/default/files/tex_cache/73210089274b7b156d38be13ddcca30a.png) .
.
Рассмотрим два варианта построения графиков (см. листинг 4.4).
% __________________Способ первый _____________________________ x=-3*pi( ):pi( )/20:3*pi( );% Формируем массив x. y= exp(sin(x)); % Формируем массив y. u= exp(cos(x/3));% Формируем массив u. v= exp(sin(x/2) );% Формируем массив v. % Строим график функции y(x), сплошная чёрная линия, без маркера, % в качестве легенды выводимЛистинг 4.4. Построение графиков (пример 4.4).. plot(x, y, "k;e^{sin(x)};") hold on;% Блокируем режим очистки окна. % Строим график функции u(x), сплошная чёрная линия, c маркером % треугольником, размер маркера — 4, в качестве легенды выводим
. plot(x, u, "->k; e^{cos(x/3)};", "markersize", 4) % Строим график функции v(x), сплошная чёрная линия, c маркером % окружностью, размер маркера — 4, в качестве легенды выводим
. plot(x, v, "-ok;e^{sin(x/2)};", "markersize", 4 ); % __________________Способ второй _____________________________ x=-3*pi( ):pi( )/20:3*pi( ); y= exp(sin(x)); u= exp(cos(x/3)); v= exp(sin(x/2)); % Отличие вывода трёх графиков состоит в том, вместо 3-х функций plot и % двух hold on используется одна функция plot в которой указаны те же % параметры вывода графиков, что и в листинге 4.4 plot(x, y, "k;e^{sin(x)};", x, u, "->k;e^{cos(x/3)};", "markersize" , 4, x, v, "-ok;e^{sin(x/2)};", "markersize", 4)
На рис. 4.5. изображены графики функций: 
Оба способа формируют один и тот же график (см. рис. 4.5).
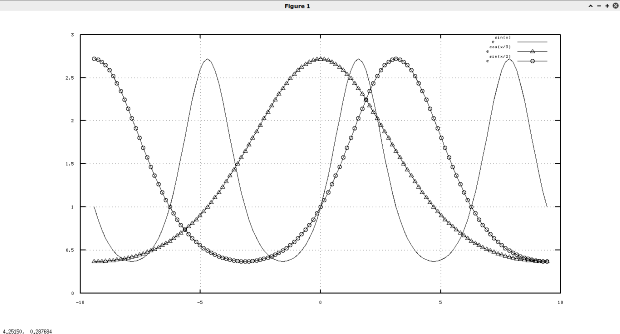
Пример 4.5. Построить график функции  на интервале [-2; 2].
на интервале [-2; 2].
В связи с тем, что функция не определена в точке 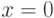 , будем строить её как графики двух функций
, будем строить её как графики двух функций 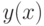 на полуинтервале [-2; 0) и
на полуинтервале [-2; 0) и 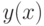 на полуинтервале (0; 2]. Текст программы на Octave с комментариями приведён в листинге 4.5, график функции — на рис. 4.6.
на полуинтервале (0; 2]. Текст программы на Octave с комментариями приведён в листинге 4.5, график функции — на рис. 4.6.
a =1;b= -0.4; c =0.05; x1 = _2:0.01: _0.1; % Определяем аргумент (массив x) на [-2;-_0.1]. x2 = 0.1:0.01:2; % Определяем аргумент (массив x) на [0.1; 2]. y1=a+b./x1+c./x1./x1; % Вычисляем значение функции y(x) на [_2; _0.1]. y2=a+b./x2+c./x2./x2; % Вычисляем значение функции y(x) на [0.1; 2]. % Строим график как график двух функций, на интервалах [-2; -0.1], [0.1; 2], % цвет графика чёрный, легенда — . plot(x1, y1, ’k;f(x)=a+b/x+c/x^2;’, x2, y2, ’k’); title(’y=f(x)’);% Подпись над графиком. xlabel(’X’); % Подпись оси X. ylabel(’Y’);% Подпись оси Y. grid on; % Рисуем линии сетки.Листинг 4.5. Построение графика (пример 4.5).
На рис. 4.6. изображен графики функции: 
Пример 4.6. Построить график функции 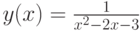 на интервале [-5; 7].
на интервале [-5; 7].
Уравнение 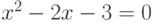 имеет корни -1, 3. Поэтому наша функция
имеет корни -1, 3. Поэтому наша функция 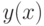 будет иметь разрывы в этих точках
будет иметь разрывы в этих точках 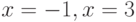 . Будем строить её, как графики трёх функций, на трёх интервалах [-5; _1.1], [0.9; 2.9], [3.1; 7]. Листинг 4.6 демонстрирует решение примера 4.6, а на рис. 4.7 изображён график функции
. Будем строить её, как графики трёх функций, на трёх интервалах [-5; _1.1], [0.9; 2.9], [3.1; 7]. Листинг 4.6 демонстрирует решение примера 4.6, а на рис. 4.7 изображён график функции 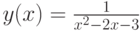 как результат работы этой программы.
как результат работы этой программы.
% Определяем аргументы на интервалах [-5; -1.1], [0.9; 2.9], [3.1; 7]. x1 = -5:0.01: -1.1; x2 = -0.9:0.01:2.9; x3 = 3.1:0.01:7; % Вычисляем значение y(x) на соответствующих интервалах. y1 =1./( x1.* x1-2*x1-3); y2 =1./( x2.* x2-2*x2-3); y3 =1./( x3.* x3-2*x3-3); % Строим график чёрного цвета, как график 3-х функций. plot(x1, y1, ’k’, x2, y2, ’k’, x3, y3, ’k’); title(’y=f(x)’); % Подпись над графиком. xlabel(’X’); % Подпись оси X. ylabel(’Y’);. % Подпись оси Y. legend(’f(x)=1/(x^2-2x-3)’, 4); % Вывод легенды. grid on; % Рисуем линии сетки.Листинг 4.6. Построение графика (пример 4.6).
На рис. 4.7. изображен график функции: 
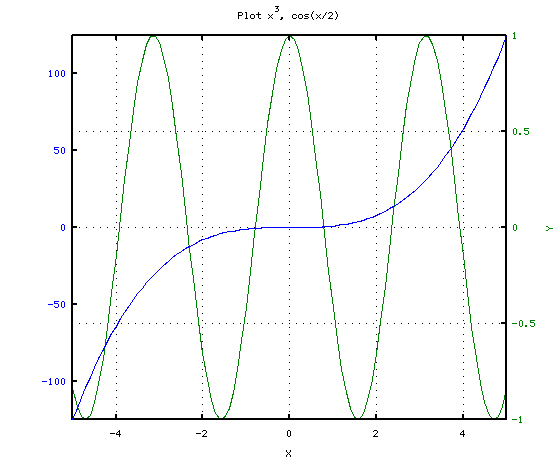
Ещё одну интересную возможность построения двух графиков предоставляет функция  , которая позволяет изображать на графике две оси ординат, что очень удобно при построении графиков разных порядков. К сожалению эта функция не позволяет явно задавать типы изображаемых линий. На каждой из осей ординат подписи значений выводятся тем же цветом, что и график функции. Использование функции plotyy рассмотрено ниже.
, которая позволяет изображать на графике две оси ординат, что очень удобно при построении графиков разных порядков. К сожалению эта функция не позволяет явно задавать типы изображаемых линий. На каждой из осей ординат подписи значений выводятся тем же цветом, что и график функции. Использование функции plotyy рассмотрено ниже.
Пример 4.7. Построить графики функции  на интервале [-5; 5].
на интервале [-5; 5].
Решение этой задачи представлено в листинге 4.7, полученный график — на рис. 4.8.
x = -5:0.1:5; y=x.^3; z=cos(2*x); plotyy(x, y, x, z); grid on; title(’Plot x^3, cos(x/2)’); xlabel(’X’); ylabel(’Y’);Листинг 4.7.
На рис. 4.8. изображены графики функций: 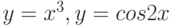
Octave предоставляет возможность построить несколько осей в графическом окне и вывести на каждую из них свои графики. Для этого следует использовать функцию subplot: subplot(row, col, cur);
Параметры  и
и  определяют количество графиков по вертикали и горизонтали соответственно,
определяют количество графиков по вертикали и горизонтали соответственно, 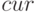 определяет номер текущего графика. Повторное обращение к функции
определяет номер текущего графика. Повторное обращение к функции 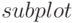 с теми же значениями
с теми же значениями  и
и 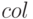 позволяет просто изменяет номер текущего графика и может использоваться для переключения между графиками. Рассмотрим использование функции
позволяет просто изменяет номер текущего графика и может использоваться для переключения между графиками. Рассмотрим использование функции 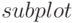 при решении следующей задачи.
при решении следующей задачи.
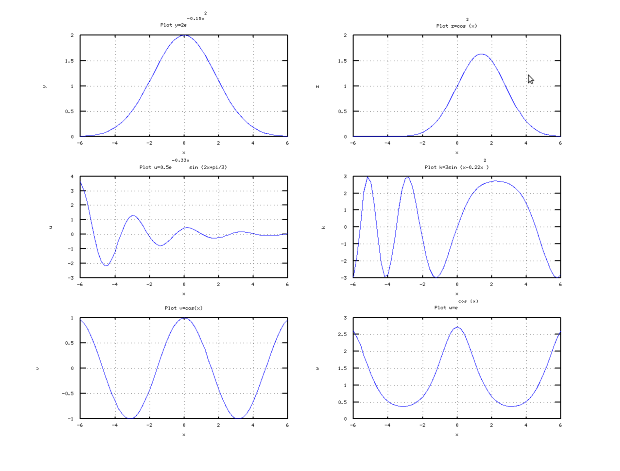
Пример 4.8. Построить графики функции 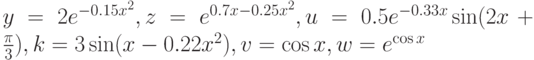 на интервале [-6; 6].
на интервале [-6; 6].
Решение задачи представлено в истинге 4.8л, полученное графическое окно — на рис. 4.9.
% Формируем массивы x, y, z, u, k, v, w.
x = -6:0.2:6; y=2*exp(*0.15* x.^2); z= exp(0.7*x-0.25* x.^2);
u=0.5*exp(-0.33*x).*sin(2*x+pi( )/3); k=3*sin(x*0.22.*x.^2);
v=cos(x);w= exp(cos(x));
% Делим графическое окно на 6 частей и объявляем первый график текущим.
subplot(3, 2, 1);
plot(x, y); % Строим график y(x) с линиями сетки и подписями.
grid on; title(’Plot y=2e^{-0.15x^2}’); xlabel(’x’); ylabel(’y’);
subplot(3, 2, 2); % Второй график объявляем текущим.
plot(x, z); % Строим график z(x) с линиями сетки и подписями.
grid on; title(’Plot z=cos^2(x)’); xlabel(’x’); ylabel(’z’);
subplot(3, 2, 3); % Третий график объявляем текущим.
plot(x, u); % Строим график u(x) с линиями сетки и подписями.
grid on; title( ’Plot u=0.5e^{-0.33x}sin (2x+pi/3)’);
xlabel(’x’); ylabel(’u’);
subplot(3, 2, 4); % Четвёртый график объявляем текущим.
plot(x, k); % Строим график k(x) с линиями сетки и подписями.
grid on; title(’Plot k=3sin(x-0.22x^2)’);
xlabel(’x’); ylabel(’k’);
subplot(3, 2, 5); % Пятый график объявляем текущим.
plot(x, v); % Строим график v(x) с линиями сетки и подписями.
grid on; title(’Plot v=cos(x)’); xlabel(’x’); ylabel(’v’);
subplot(3, 2, 6); % Шестой график объявляем текущим.
plot(x,w); % Строим график w(x) с линиями сетки и подписями.
grid on; title(’Plot w=e^{cos (x)}’ ); xlabel(’x’); ylabel(’w’);
Листинг
4.8.
Построение графиков (пример 4.8).
Для построения графика функции можно использовать функцию  следующей структуры:
следующей структуры: ![fplot(@f, [xmin, xmax], s)](/sites/default/files/tex_cache/c2ed37d94b86fafd828b68cad3740b79.png) .
.
Здесь  — имя функции (стандартной функции Octave или функции, определённой пользователем),
— имя функции (стандартной функции Octave или функции, определённой пользователем), ![[xmin, xmax]](/sites/default/files/tex_cache/0eb1b1ef0ea341f71ecec19e2ea66357.png) — интервал, на котором будет строиться график,
— интервал, на котором будет строиться график,  — строка формата, определяющая только параметры линии (но не легенду). Легенда графика формируется автоматически функцией
— строка формата, определяющая только параметры линии (но не легенду). Легенда графика формируется автоматически функцией  без использования функции
без использования функции  . Не позволяет формировать легенду и третий параметр функции
. Не позволяет формировать легенду и третий параметр функции  , в отличии от функции
, в отличии от функции 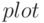 .
.
Пример 4.9. Используя функцию  , построить графики функций
, построить графики функций 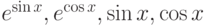 на интервале
на интервале ![[-3\pi; 2\pi]](/sites/default/files/tex_cache/7a4f0421dd2df7494ba30cb330964471.png) .
.
Текст программы на языке Octave с комментариями приведён в листинге 4.9. Полученные графики можно увидеть на рис. 4.10.
% Определяем функцию f = exp(cos(x)) function y=f(x) y=exp(cos(x)); end % Определяем функцию g = exp(sin(x)) function z=g(x) z=exp(sin(x)); end h=figure( ); % Делим графическое окно на 4 части и объявляем первый график текущим. subplot(2, 2, 1); % Строим график g = exp(cos(x)) на интервалеЛистинг 4.9. Построение графиков с помощью fplot (пример 4.9).% голубого цвета с маркером. fplot(@g, [-3*pi( ), 2*pi( )], ’-pb’); title(’Plot y=e^{cos(x)}’); % Подписываем график. grid on; % Проводим линии сетки subplot(2, 2, 2); % Второй график объявляем текущим. % Строим график f=exp(sin(x)) на интервале
% красного цвета с маркером. fplot(@f, [-3*pi( ), 2-pi( )], ’-or’); title(’Plot z=e^{sin(x)}’);% Подписываем график. grid on; % Проводим линии сетки subplot ( 2, 2, 3 ); % Третий график объявляем текущим. % Строим график sin(x) на интервале
чёрного цвета fplot(@sin, [-3*pi( ), 2*pi( )], ’k’); title(’Plot sin(x)’); % Подписываем график. grid on; % Проводим линии сетки subplot(2, 2, 4); % Четвёртый график объявляем текущим. % Строим график cos(x) на интервале
зелёного цвета fplot(@cos, [-3*pi( ), 2*pi( )], ’g’); title(’Plot cos(x)’); % Подписываем график. grid on; % Проводим линии сетки


 (точка)
(точка)