|
Возможна ли разработка приложения на Octave с GUI? |
Интегрирование и дифференцирование
Дифференцирование в Octave осуществляется в технике символьных переменных. Для работы с символьными переменными в Octave подключите специальный пакет расширений octave-symbolic. Установка пакетов расширений описана в первой главе, техника работы с символьными переменными — в п. 2.7. В функциях интегрирования реализованы различные численные алгоритмы.
8.1 Вычисление производной
Дифференцирование в Octave осуществляется с помощью функции ![differentiate(f(a,x [,n]))](/sites/default/files/tex_cache/75e9861d8d46ba69962ba7fb06a4ad26.png) , где
, где  — символьное выражение,
— символьное выражение,  — переменная дифференцирования,
— переменная дифференцирования,  — порядок дифференцирования (при
— порядок дифференцирования (при 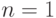 параметр можно опустить). Иными словами, функция вычисляет
параметр можно опустить). Иными словами, функция вычисляет  -ю производную выражения
-ю производную выражения  по переменной
по переменной  .
.
Производной функции  в точке
в точке  называется предел, к которому стремится отношение бесконечно малого приращения функции к соответствующему бесконечно малому приращению аргумента. Геометрический смысл этого понятия заключается в том, что если к графику функции
называется предел, к которому стремится отношение бесконечно малого приращения функции к соответствующему бесконечно малому приращению аргумента. Геометрический смысл этого понятия заключается в том, что если к графику функции  провести касательную в точке
провести касательную в точке  , то её угловой коэффициент, будет равен значению производной в этой точке
, то её угловой коэффициент, будет равен значению производной в этой точке 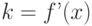 . Следовательно, уравнение касательной к линии в заданной точке имеет вид:
. Следовательно, уравнение касательной к линии в заданной точке имеет вид: 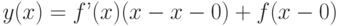
Пример 8.1. Записать уравнение касательной к функции , в точке
, в точке 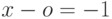 .
.
Из листинга 8.1 видим, что уравнение касательной к функции в заданной точке имеет вид y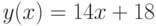 .
.
clear all;
x0=-1;
symbols
x = sym("x");
f =(3 - x^2-7) /(2 - x+1);
f1=differentiate(f,x)% Первая производная от заданной функции
% Уравнение касательной: k=subs(f1,x,x0), f(x0)=subs(f,x,x0)
y=subs (f1, x, x0) - (x-x0)+subs(f, x, x0)
f1 =(6.0)*x*(1.0+(2.0)*x)^(-1)-(2.0)*(-7.0+(3.0)*x^(2.0))*(1.0+(2.0)*x)^(-2)
y =18.0-9.029803704631804845E-19*I+(14.0-6.0198691364212032297E-19*I)*x
Листинг
8.1.
Получение уравнения касательной (пример 8.1).
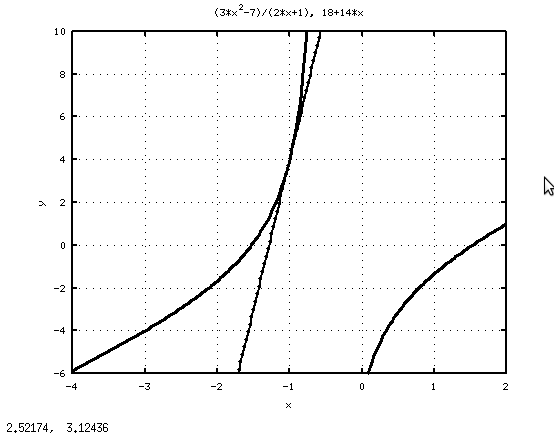
На рис. 8.1 представлены графики заданной функции и её касательной. Рисунок построен с помощью команд из листинга 8.2.
clear all; clf; cla;
symbols
x=sym ("x");
L1=ezplot(’(3*x^2-7)/(2*x+1)’);
set(L1, ’LineWidth’, 3, ’Color’, ’k’)
hold on
L2=ezplot(’18+14*x’);
set(L2, ’LineWidth’, 2, ’Color’, ’k’, ’Marker’, ’o’)
set(gca, ’xlim’, [-4, 2]); set(gca, ’ylim’, [-6, 10]);
set(gca, ’xtick’, [-4:2]); set(gca, ’ytick’, [-6:2:10]);
grid on; xlabel(’x’); ylabel(’y’);
title(’(3*x^2-7)/(2*x+1), 18+14*x’);
Листинг
8.2.
График функции и её касательной (пример 8.1).
Пример 8.2. Найти a) 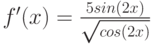 и б)
и б) ![f'(x)=tan\sqrt[3]{ln(x)}](/sites/default/files/tex_cache/3b884370997cf852dd001590c7de59b2.png) .
.
Решение примера показано влистинге 8.3.
>>> clear all;
>>> symbols
>>> x = sym("x");
% Пример а)
>>> f =(5- Sin(2 - x))/Sqrt(Cos(2 - x));
>>> f1=differentiate(f, x)
f1 =(5.0)*sin((2.0)*x)^2*cos((2.0)*x)^(-3/2)+(10.0)*sqrt(cos((2.0)*x))
% Пример б)
>>> f=Tan(Log(x)^(1/3));
>>> f1=differentiate(f, x)
f1 = (0.333)*(1+tan(log(x)^(0.333))^2)*x^(-1)*log(x)^(-0.666)
Листинг
8.3.
Нахождение производных (пример 8.2).
Если функция 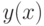 задана параметрическими уравнениями
задана параметрическими уравнениями 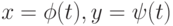 , то производная вычисляется по формуле
, то производная вычисляется по формуле 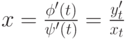
Пример 8.3. Найти производную функции, заданной параметрически:
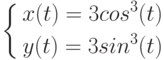
Листинг 8.4 содержит решение примера.
>>> clear all;
>>> symbols
>>> t = sym("t");
>>> x=3-Cos(t)^3;
>>> y=3-Sin(t)^3;
>>> xt=differentiate(x, t);
>>> yt=differentiate(y, t);
>>> f=yt/xt
f = -sin(t) - cos(t) ^( -1.0)
Листинг
8.4.
Производная параметрической функции (пример 8.3).
Пример 8.4. Найти производные a) 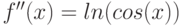 б)
б)  (Листинг 8.5).
(Листинг 8.5).
>>> clear all;
>>> symbols
>>> x=sym("x");
% Пример а)
>>> f=Log(Cos(x));
>>> differentiate(f, x, 2)
ans = -1-cos(x)^(-2)-sin(x)^2
% Пример б)
>>> f=Tan(x);
>>> differentiate(f, x, 4)
ans = 16-(1+tan(x)^2)^2-tan(x)+8-(1+tan(x)^2)-tan(x)^3
Листинг
8.5.
Производные высших порядков (пример 8.4).
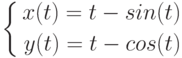
Выражение для вычисления второй производной параметрической функции: 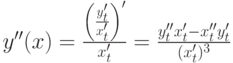 .
.
В листинге 8.6 представлено решение примера
>>> clear all;
>>> symbols
>>> t=sym("t");
>>> x=t-Sin(t);
>>> y=1-Cos(t);
>>> xt=differentiate(x, t);
>>> yt=differentiate(y, t);
>>> xt2=differentiate(x, t, 2);
>>> yt2=differentiate(y, t, 2);
>>> z=(yt2-xt-xt2-yt)/xt^3
z=-(1-cos(t))^(-3.0)-(cos(t)-(-1+cos(t))+sin(t)^2)
Листинг
8.6.
Вторая производная параметрической функции (пр. 8.5).