|
Возможна ли разработка приложения на Octave с GUI? |
Интегрирование и дифференцирование
8.3.2 Интегрирование по методу Симпсона
Изложим идею интегрирования по методу Симпсона. Пусть 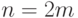 — чётное число, а
— чётное число, а  — значения функции
— значения функции  для равноотстоящих точек
для равноотстоящих точек  с шагом
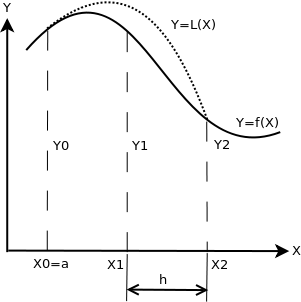
с шагом 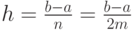 . На паре соседних участков (рис. 8.6) кривая
. На паре соседних участков (рис. 8.6) кривая  заменяется параболой
заменяется параболой 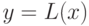 , коэффициенты которой подобраны так, что она проходит через точки
, коэффициенты которой подобраны так, что она проходит через точки 
Площадь криволинейной трапеции, ограниченной сверху параболой, составит: 
Суммируя площади всех криволинейных трапеций, получим:
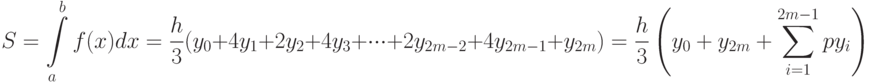
,
где1Как нетрудно заметить  при чётном
при чётном  и
и 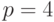 при нечётном
при нечётном  .
.

Следовательно, формула Симпсона для численного интегрирования имеет вид:
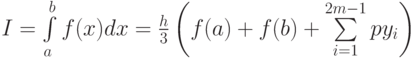
Методы трапеций и Симпсона являются частными случаями квадратурных формул Ньютона–Котеса, которые, вообще говоря, имеют вид,
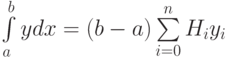
где 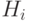 — это некоторые константы называемые постоянными Ньютона–Котеса.
— это некоторые константы называемые постоянными Ньютона–Котеса.
Если для квадратурных формул Ньютона-Котеса принять 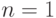 , то получим метод трапеций, а при
, то получим метод трапеций, а при 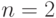 — метод Симпсона. Поэтому эти методы называют квадратурными методами низших порядков. Для
— метод Симпсона. Поэтому эти методы называют квадратурными методами низших порядков. Для 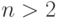 получают квадратурные формулы Ньютона–Котеса высших порядков.
получают квадратурные формулы Ньютона–Котеса высших порядков.
В Octave реализован вычислительный алгоритм метода Симпсона с автоматическим выбором шага. Автоматический выбор шага интегрирования заключается в том, что интервал интегрирования разбивают на n отрезков и вычисляют значение интеграла, если полученное значение не удовлетворяет заданной точности вычислений, то n увеличивают вдвое и вновь вычисляют значение интеграла, так повторяют до тех пор пока не будет достигнута заданная точность. Итак, вычисление интеграла по методу Симпсона обеспечивает функция ![[F, K] = quadv(name, a, b[, tol, trace])](/sites/default/files/tex_cache/0e8bb72367287ed55ae4f7e84890d5d2.png) , где:
, где:
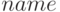 — имя функции, задающей подынтегральное выражение;
— имя функции, задающей подынтегральное выражение;
 — пределы интегрирования;
— пределы интегрирования;
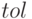 — точность вычислений;
— точность вычислений;
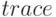 — параметр позволяющий получить информацию о ходе вычислений в виде таблицы, в столбцах которой представлены: значение количества вычислений, начальная точка текущего промежутка интегрирования, его длина и значение интеграла;
— параметр позволяющий получить информацию о ходе вычислений в виде таблицы, в столбцах которой представлены: значение количества вычислений, начальная точка текущего промежутка интегрирования, его длина и значение интеграла;
 — значение интеграла;
— значение интеграла;
 — количество итераций.
— количество итераций.
Пример 8.13. Вычислить интеграл 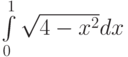
Решение примера с применением функции 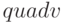 приведено влистинге 8.15.
приведено влистинге 8.15.
% Подынтегральная функция function y=G(x) y=(4-x^2).^(1/2); end; >>> format long % Вычисление интеграла по методу Симпсона % Точность установлена по умолчанию 1.0e-06 >>> [F1, K1]=quadv(’G’, 0, 1) % Результат — значение интеграла и количество итераций F1 = 1.91322288999134 K1 = 17 % Точность установлена пользователем 1.0e-07 >>> [F2, K2]=quadv(’G’, 0, 1, 1.0 e-07) % Результат — значение интеграла и количество итераций F2 = 1.91322295090669 K2 = 33 >>> format short % Вызов функций с заданной степенью точности % Вывод дополнительной информации о вычислениях >>> quadv (’G’, 0, 1, 1.0 e-05,5) 5.00000 0.00000 1.00000 1.91321 7.00000 0.00000 0.50000 0.98948 9.00000 0.50000 0.50000 0.92374 11.0000 0.50000 0.25000 0.47458 13.0000 0.75000 0.25000 0.44916 ans = 1.9132Листинг 8.15. Вычисление интеграла через quadv (пример 8.13).