Решение обыкновенных дифференциальных уравнений и систем

9.1 Общие сведения о дифференциальных уравнениях

Дифференциальным уравнением -го порядка называется соотношение вида

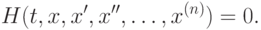( 9.1)

Решением дифференциального уравнения называется функция 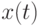, которая обращает уравнение в тождество.

Системой дифференциальных уравнений -го порядка называется система вида:

( 9.2)

Системой линейных дифференциальных уравнений называется система вида:

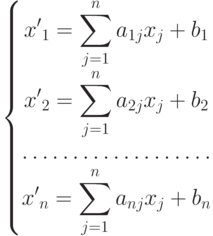( 9.3)

Решением системы называется вектор 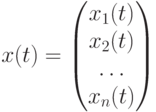, который обращает уравнения систем (9.2), (9.3) в тождества.

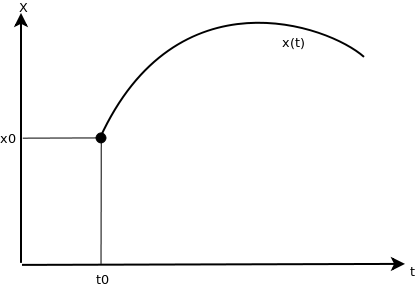
Каждое дифференциальное уравнение, так же, как и система, имеет бесконечное множество решений, которые отличаются друг от друга константами. Для однозначного определения решения необходимо определить дополнительные начальные или граничные условия. Количество таких условий должно совпадать с порядком дифференциального уравнения или системы. В зависимости от вида дополнительных условий в дифференциальных уравнениях различают:

• задачу Коши, в случае, если все дополнительные условия заданы в одной (чаще начальной) точке интервала;
• краевую задачу, в случае, когда дополнительные условия заданы на границах интервала.

Различают точные (аналитические) и приближённые (численные) методы решения дифференциальных уравнений. Большое количество уравнений может быть решено точно. Однако есть уравнения, а особенно системы уравнений, для которых нельзя записать точное решение. Но даже для уравнений с известным аналитическим решением очень часто необходимо вычислить числовое значение при определённых исходных данных. Поэтому широкое распространение получили численные методы решения обыкновенных дифференциальных уравнений.

Рис. 9.1. Интегральная кривая, проходящая через точку M_0(_t0, x_0)