|
Возможна ли разработка приложения на Octave с GUI? |
Нелинейные уравнения и системы
В общем случае аналитическое решение уравнения 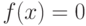 можно найти только для узкого класса функций. Чаще всего приходится решать это уравнение численными методами. Численное решение уравнения проводят в два этапа. На первом этапе отделяют корни уравнения, т.е. находят достаточно тесные промежутки, в которых содержится только один корень. Эти промежутки называют интервалами изоляции корня. Определить интервалы изоляции корня можно, например, изобразив график функции. Идея графического метода основана на том, что непрерывная функция
можно найти только для узкого класса функций. Чаще всего приходится решать это уравнение численными методами. Численное решение уравнения проводят в два этапа. На первом этапе отделяют корни уравнения, т.е. находят достаточно тесные промежутки, в которых содержится только один корень. Эти промежутки называют интервалами изоляции корня. Определить интервалы изоляции корня можно, например, изобразив график функции. Идея графического метода основана на том, что непрерывная функция  имеет на интервале
имеет на интервале ![[a, b]](/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png) хотя бы один корень, если она поменяла на этом интервале знак:
хотя бы один корень, если она поменяла на этом интервале знак: 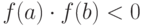 . Границы интервала
. Границы интервала  и
и  называют пределами интервала
изоляции1Графический метод весьма приблизителен, отделить корни для функции
называют пределами интервала
изоляции1Графический метод весьма приблизителен, отделить корни для функции 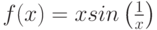 , при
, при 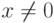 и
и 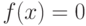 при
при 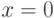 ни на каком интервале, содержащем нуль
ни на каком интервале, содержащем нуль 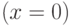 таким способом не удастся. (Прим. редактора).. На втором этапе проводят уточнение отделённых корней, т.е. находят корни с заданной точностью.
таким способом не удастся. (Прим. редактора).. На втором этапе проводят уточнение отделённых корней, т.е. находят корни с заданной точностью.
7.1 Решение алгебраических уравнений
Любое уравнение 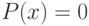 , где
, где 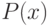 это многочлен (полином), отличный от нулевого, называется алгебраическим уравнением относительно переменной
это многочлен (полином), отличный от нулевого, называется алгебраическим уравнением относительно переменной  . Всякое алгебраическое уравнение относительно
. Всякое алгебраическое уравнение относительно  можно записать в виде
можно записать в виде

 — коэффициенты алгебраического уравнения
— коэффициенты алгебраического уравнения  –й степени. Например, линейное уравнение это алгебраическое уравнение первой степени, квадратное — второй, кубическое — третьей и так далее.
–й степени. Например, линейное уравнение это алгебраическое уравнение первой степени, квадратное — второй, кубическое — третьей и так далее.
В Octave определить алгебраическое уравнение можно в виде вектора его коэффициентов  . Например, полином
. Например, полином 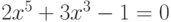 задаётся вектором:
задаётся вектором:
>>> p =[2,0,3,0, -1] p = 2 0 3 0 -1
Рассмотрим функции, предназначенные для действий над многочленами.
Произведение двух многочленов вычисляет функция  , где
, где 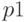 — многочлен степени
— многочлен степени  ,
,  — многочлен степени
— многочлен степени  . Функция формирует вектор
. Функция формирует вектор  , соответствующий коэффициентам многочлена степени
, соответствующий коэффициентам многочлена степени 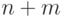 , полученного в результате умножения
, полученного в результате умножения 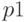 на
на  .
.
Пример 7.1. Определить многочлен, который получится в результате умножения выражений 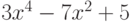 и
и 
Как видно из листинга 7.1 в результате имеем: 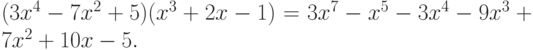
>>> p1=[3 0 -7 0 5]; >>> p2=[1 0 2 -1]; >>> p=conv (p2, p1) p = 3 0 -1 -3 -9 7 10 -5Листинг 7.1. Умножение многочленов (пример 7.1).
Частное и остаток от деления двух многочленов находит функция ![[q, r] = deconv(p1, p2)](/sites/default/files/tex_cache/d86d596c23bb2e3169c3a5bf2bb84378.png) , здесь,
, здесь, 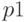 — многочлен степени
— многочлен степени 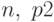 — многочлен степени
— многочлен степени  . Функция формирует вектор
. Функция формирует вектор  — коэффициенты многочлена, который получается в результате деления
— коэффициенты многочлена, который получается в результате деления 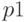 на
на  и вектор
и вектор  — коэффициенты многочлена, который является остатком от деления
— коэффициенты многочлена, который является остатком от деления 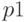 на
на  .
.
Пример 7.2. Найти частное и остаток от деления многочлена  на многочлен
на многочлен 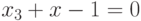 .
.
В результате имеем (см. листинг 7.2):
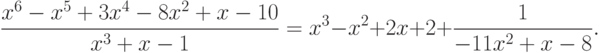
>>> p1=[1 -1 3 0 -8 1 -10]; >>> p2=[1 0 1 -1]; >>> [q, r]=deconv(p1, p2) q = 1 -1 2 2 r = 0 0 0 0 -11 1 -8Листинг 7.2. Деление многочленов (пример 7.2).
Выполнить разложение частного двух многочленов, представляющих собой правильную дробь на простейшие рациональные дроби вида

можно с помощью функции ![[a, b, c, k] = residue(p1, p2)](/sites/default/files/tex_cache/db0d6bb2fb90a85e5cf55b7903c9a9dd.png) , где
, где 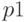 — многочлен степени
— многочлен степени  (числитель),
(числитель),  — многочлен степени
— многочлен степени  (знаменатель), причём
(знаменатель), причём  .
.
В результате работы функция формирует четыре вектора:  — вектор коэффициентов, расположенных в числителях простейших дробей,
— вектор коэффициентов, расположенных в числителях простейших дробей,  — вектор коэффициентов, расположенных в знаменателях простейших дробей,
— вектор коэффициентов, расположенных в знаменателях простейших дробей,  — вектор степеней знаменателей простейших дробей (кратность),
— вектор степеней знаменателей простейших дробей (кратность),  — вектор коэффициентов остаточного члена.
— вектор коэффициентов остаточного члена.
Пример 7.3. Разложить выражение 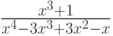 на простейшие дроби.
на простейшие дроби.
Проанализировав листинг 7.3 запишем решение:
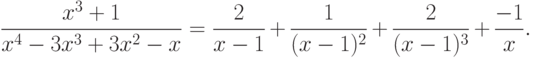
Значение вектора ](/sites/default/files/tex_cache/5a642f8046142048121b0349ba33dde1.png) говорит об отсутствии остаточного члена.
говорит об отсутствии остаточного члена.
>>> p1=[1 0 0 1 ]; >>> p2=[1 -3 3 -1 0]; >>> [a, b, c, k]= residue (p1, p2) a = 2.00000 1.00000 2.00000 -1.00000 b = 1.00000 1.00000 1.00000 0.00000 c = [ ] ( 0 x0 ) k = 1 2 3 1Листинг 7.3. Разложение на простейшие дроби (пример 7.3).
