Интегрирование и дифференцирование

8.2 Исследование функций

Понятие производной тесно связано с задачей исследования функции. Из курса математического анализа известно, что если производная функции положительна на всём интервале , то функция на нём возрастает, если всюду отрицательна, то убывает.

Пример 8.6. Построить график функции и её производной. Исследовать функцию на возрастание и убывание.

Вычислим производную заданной функции и построим оба графика в одном окне :

	
>>> symbols
>>> x=sym("x");
>>> f=1-2-x-x^2;
>>> differentiate(f, x)
ans=-2.0-(2.0)-x
% построим график заданной функции и её производной.
clf; cla;
L1=ezplot(’1-2*x-x^2’); set(L1, ’LineWidth’, 3, ’Color’, ’k’)
hold on
L2=ezplot(’-2-2*x’); set(L2, ’LineWidth’, 2, ’Color’, ’k’)
grid on; xlabel(’x’); ylabel(’y’); title(’1-2x-x^2, -2-2x’)

На рис. 8.2 видим, что там, где 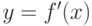принимает положительные значения, возрастает, соответственно, при отрицательныхзначениях 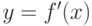функция убывает.

Говорят, что непрерывная функция имеет максимум в точке 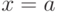, если в достаточной близости от этой точки производная 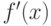положительна слева от a и отрицательна справа от a. Если наоборот, то имеет минимум в точке 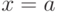. Максимум и минимум объединяют названием экстремум. Если первая производная в этой точке либо равна нулю, либо не существует, то в этой точке может быть экстремум.

Пример 8.7. Исследовать функцию на экстремум.

Найдём производную функции и отобразим её на графике:

	
clear all;
symbols
x=sym("x");
f=x^3/3-2-x^2+3-x+1;
% Производная от функции f(x)
y=differentiate(f, x)
y=3.0+x^(2.0)-(4.0)-x
% Изобразим функцию и её производную на графике
clf; cla;
L1=ezplot(’x^3/3-2*x^2+3*x+1’);
set(L1, ’LineWidth’, 3, ’Color’, ’k’)
hold on
L2=ezplot(’3.0+x^(2.0)-(4.0)*x’);
set(L2, ’LineWidth’, 2, ’Color’, ’k’)
set(gca, ’xlim’, [-2,5]); set(gca, ’ylim’, [-5,5]);
grid on; xlabel(’x’); ylabel(’y’);
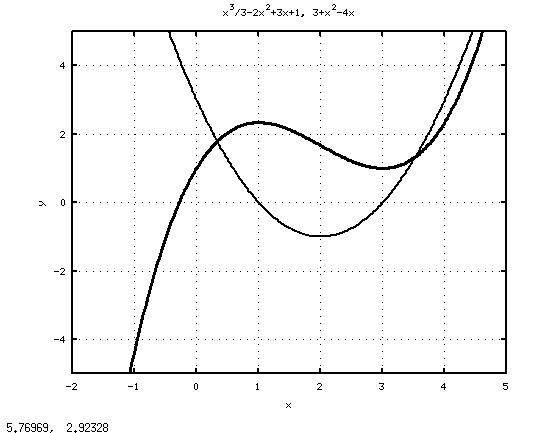
title(’x^3/3-2x^2+3x+1, 3+x^2-4x’)
% Корни уравнения
>>> x1 = symfsolve(y, 1)
>>> x2 = symfsolve(y, 3)
x1 = 1
x2 = 3

На рис. 8.3 и в листинге 8.8 видно, что первая производная обращается в нуль в точках и . При переходе через точку меняет знак с плюса на минус, следовательно, это точка максимума функции , а в точке знак первой производной меняется с минуса на плюс, то есть это точка минимума.

График функции называется выпуклым на промежутке , если он расположен выше касательной, проведённой в любой точке этого интервала. Если же график функции лежит ниже касательной, то он называется вогнутым. Функция будет выпуклой на интервале , если вторая производная 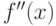на нём положительна. И наоборот, если вторая производная отрицательна, то функция вогнута. Если же вторая производная равна нулю в некоторой точке , а слева и справа от неё имеет значения разных знаков, то точка — точка перегиба.

Рис. 8.3. Исследование функции на экстремум

Пример 8.8. Определить точки перегиба функции

Найдём вторую производную заданной функции. Построим графики функции и её второй производной. Определим точки в которых вторая производная обращается в ноль (листинг 8.9).

	
clear all;
symbols
x=sym("x");
f=(3-x-2)/(x^2+1);
y=differentiate(f, x, 2)
y=-(2.0)*(1.0+x^(2.0))^(-2)*(-2.0+(3.0)*x)-(12.0)*(1.0+x^(2.0))^(-2)
	*x+(8.0)*(1.0+x^(2.0))^(-3)*x^2*(-2.0+(3.0)*x)
clf; cla;
L1=ezplot(’(3*x-2)/(x^2+1)’); set(L1, ’LineWidth’, 4, ’Color’, ’k’)
hold on
L2=ezplot(’-(2.0)*(1.0+x^(2.0))^(-2)*(-2.0+(3.0)*x)-(12.0)*(1.0+x^(2.0))^(-2)
	*x+(8.0)*(1.0+x^(2.0))^(-3)*x^2*(-2.0+(3.0)*x)’);
set(L2, ’LineWidth’, 2, ’Color’, ’k’)
set(gca, ’xlim’, [-5, 5]); set(gca, ’ylim’, [-5, 7]);
grid on; xlabel(’x’); ylabel(’y’); title(’ ’)
>>> x1 = symfsolve(y, -1)
>>> x2 = symfsolve(y, 0)
>>> x3 = symfsolve(y,2)
x1 = -1.1411
x2 = 0.19855
x3 = 2.9425

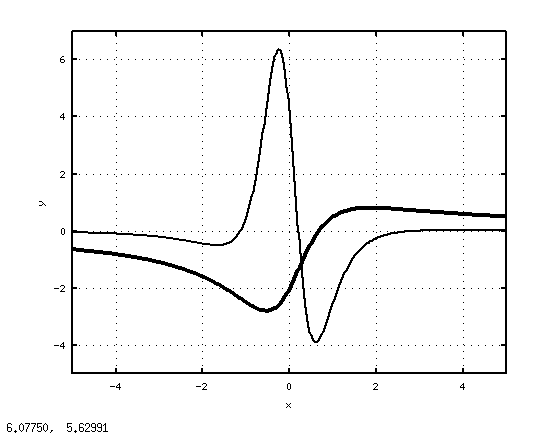
Рис. 8.4. Определение точки перегиба функции

Иллюстрации приведены на рис. 8.4. Исследование второй производной функции 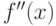показывает, что она определена на всей числовой оси и обращается в нуль в трёх точках , причём при переходе через них она меняет знак. Следовательно, на интервале функция вогнутая, так как , на — выпуклая , на — вогнутая и на опять выпуклая, потому что .