|
Возможна ли разработка приложения на Octave с GUI? |
Построение графиков
4.2 Построение трёхмерных графиков
График поверхности (трёхмерный или 3D-график) — это график, положение точки в котором определяется значениями трёх координат.
4.2.1 Построение графиков поверхностей
Дадим определение прямоугольной (или декартовой) системы координат в пространстве.
Прямоугольная система координат в пространстве состоит из заданной фиксированной точки  пространства, называемой началом координат, и трёх перпендикулярных прямых пространства
пространства, называемой началом координат, и трёх перпендикулярных прямых пространства 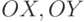 и
и 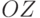 , не лежащих в одной плоскости и пересекающихся в начале координат, — их называют координатными осями (
, не лежащих в одной плоскости и пересекающихся в начале координат, — их называют координатными осями (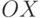 — ось абсцисс,
— ось абсцисс, 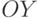 — ось ординат,
— ось ординат, 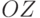 — ось аппликат). Положение точки
— ось аппликат). Положение точки  в пространственной системе координат определяется значением трёх координат и обозначается
в пространственной системе координат определяется значением трёх координат и обозначается 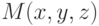 . Три плоскости, содержащие пары координатных осей, называются координатными плоскостями
. Три плоскости, содержащие пары координатных осей, называются координатными плоскостями  и
и 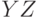 .
.
Величина  называется функцией двух величин
называется функцией двух величин  и
и  , если каждой паре чисел, которые могут быть значениями переменных
, если каждой паре чисел, которые могут быть значениями переменных  и
и  , соответствует одно или несколько определённых значений величины
, соответствует одно или несколько определённых значений величины  . При этом переменные
. При этом переменные  и
и  называют аргументами функции
называют аргументами функции 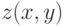 . Пары тех чисел, которые могут быть значениями аргументов
. Пары тех чисел, которые могут быть значениями аргументов  ,
,  функции
функции 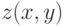 , в совокупности составляют область определения этой функции.
, в совокупности составляют область определения этой функции.
Для построения графика двух переменных 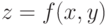 необходимо выполнить следующие действия.
необходимо выполнить следующие действия.
- Сформировать в области построения графика прямоугольную сетку, проводя прямые, параллельные осям
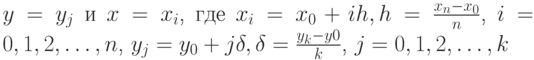 .
. - Вычислить значения
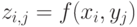 во всех узлах сетки.
во всех узлах сетки. - Обратиться к функции построения поверхности, передавая ей в качестве параметров сетку и матрицу
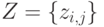 значений в узлах сетки.
значений в узлах сетки.
Для формирования прямоугольной сетки в Octave есть функция 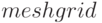 . Рассмотрим построение трёхмерного графика на следующем примере.
. Рассмотрим построение трёхмерного графика на следующем примере.
Пример 4.14. Построить график функции ![z(x,y)=3x^{2}-2sin^{2}y, x \in [-2,2], y \in [-3,3]](/sites/default/files/tex_cache/a6580b9a11fc07330aaa5ba9c4141719.png) .
.
Для формирования сетки воспользуемся функцией 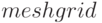 .
.
>>>[x y]=meshgrid(-2:2,-3:3) x = -2 -1 0 1 2 -2 -1 0 1 2 -2 -1 0 1 2 -2 -1 0 1 2 -2 -1 0 1 2 -2 -1 0 1 2 -2 -1 0 1 2 y = -3 -3 -3 -3 -3 -2 -2 -2 -2 -2 -1 -1 -1 -1 -1 0 0 0 0 0 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3
После формирования сетки вычислим значение функции во всех узловых точках
>>> z=3*x.*x-2*sin(y).^2 z = 11.96017 2.96017 -0.03983 2.96017 11.96017 10.34636 1.34636 -1.65364 1.34636 10.34636 10.58385 1.58385 -1.41615 1.58385 10.58385 12.00000 3.00000 0.00000 3.00000 12.00000 10.58385 1.58385 -1.41615 1.58385 10.58385 10.34636 1.34636 -1.65364 1.34636 10.34636 11.96017 2.96017 -0.03983 2.96017 11.96017Листинг .
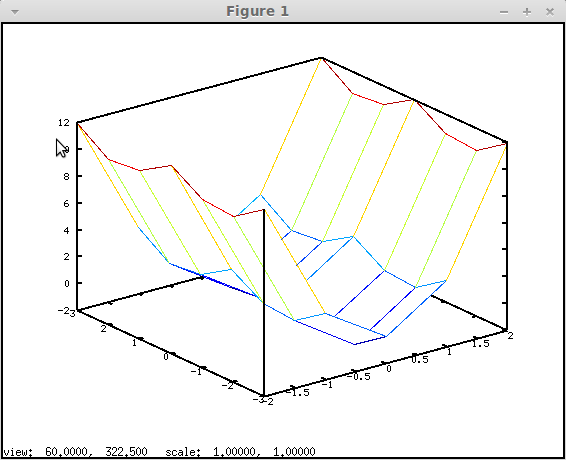
На рис. 4.17. изображен график функции: 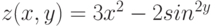
Для построения каркасного графика следует обратиться к функции  ;
;
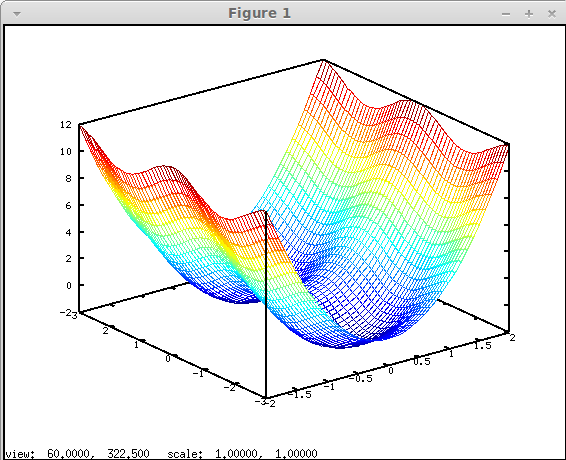
После это будет создано графическое окно с трёхмерным графиком (см. рис. 4.17). Как видно, полученный график получился грубым, для получения менее грубого графика следует сетку сделать более плотной (см. листинг 4.14 и рис. 4.18).
[x y]= meshgrid(- 2:0.1:2, -3:0.1:3); z=3*x.*x-2*sin(y).^2 mesh(x, y, z);Листинг 4.14. Построение графика поверхности (пример 4.14).
Любой трёхмерный график можно вращать, используя мышку.
Для построения поверхностей, кроме функции  построения каркасного графика, есть функция
построения каркасного графика, есть функция 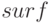 , которая строит каркасную поверхность, заливая её каждую клетку цветом, который зависит от значения функции в узлах сетки.
, которая строит каркасную поверхность, заливая её каждую клетку цветом, который зависит от значения функции в узлах сетки.
Пример 4.15. С использованием функции 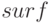 построить график функции
построить график функции  .
.
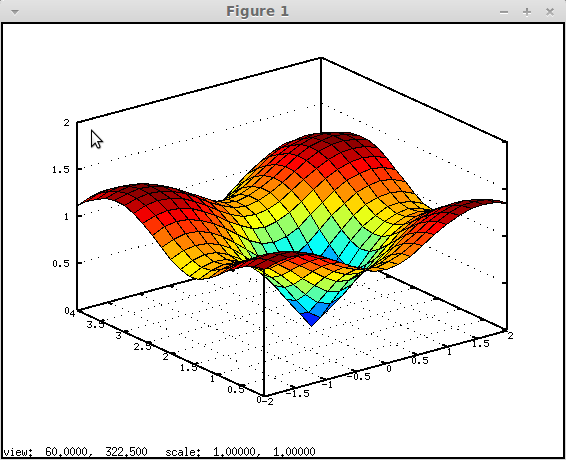
В листинге 4.15 представлено решение задачи, а на рис. 4.19 изображён получившийся график.
На рис. 4.18. изображен график функции: 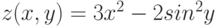
[x y]= meshgrid(-2:0.2:2, 0:0.2:4); z=sqrt(sin(x).^2+cos(y).^2); surf(x, y, z);Листинг 4.15. Построение графика поверхности (пример 4.15).
В Octave можно построить графики двух поверхностей в одной системе координат, для этого, как и для плоских графиков, следует использовать команду 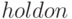 , которая блокирует создание второго нового окна при выполнении команд
, которая блокирует создание второго нового окна при выполнении команд 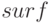 или
или  .
.
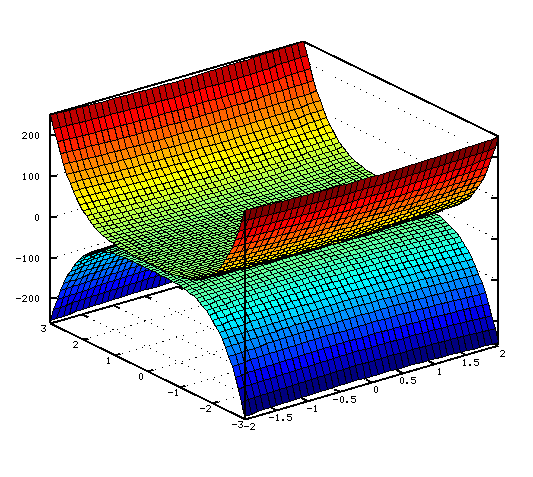
Пример 4.16. Построить в одной системе координат графики
функций 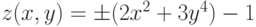 .
.
Решение задачи с использованием функции 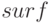 представлено в листинге 4.16, полученный график изображён на рис. 4.20.
представлено в листинге 4.16, полученный график изображён на рис. 4.20.
h=figure( ); [x y]= meshgrid(-2:0.1:2, -3:0.1:3); z=2*x.^2+3*y.^4-1; z1=-2*x.^2-3*y.^4-1; surf(x, y, z); hold on surf(x, y, z1);Листинг 4.16. Построение двух графиков одновременно (пример 4.16).
На рис. 4.19. изображен график функции: 
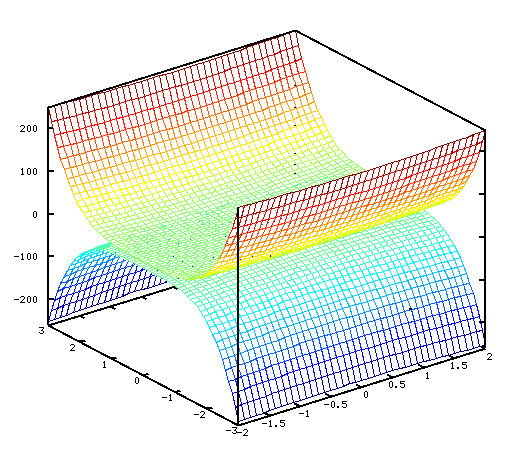
Построение поверхности с помощью функции  можно осуществить аналогично (см. листинг 4.17), графики функций — можно увидеть на рис. 4.21.
можно осуществить аналогично (см. листинг 4.17), графики функций — можно увидеть на рис. 4.21.
h=figure( ); [x y]= meshgrid(-2:0.1:2, -3:0.1:3); z=2*x.^2+3*y.^4-1; z1=-2*x.^2-3*y.^4-1; mesh(x, y, z); hold on mesh(x, y, z1);Листинг 4.17. Построение графиков с помощью mesh (пример 4.16).
4.2.2 Построение графиков поверхностей, заданных параметрически
При построении графиков поверхностей, заданных параметрически  и
и 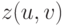 необходимо построить матрицы
необходимо построить матрицы  и
и  одинакового размера. Для этого массивы
одинакового размера. Для этого массивы  и
и  должны быть одинакового размера. Можно выделить два основных вида представления
должны быть одинакового размера. Можно выделить два основных вида представления 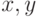 и
и  в случае параметрического задания поверхностей:
в случае параметрического задания поверхностей:
- Если
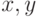 и
и  представимы в виде
представимы в виде 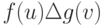 , то соответствующие им матрицы
, то соответствующие им матрицы  и
и  следует формировать в виде матричного умножения
следует формировать в виде матричного умножения 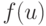 на
на 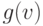 .
. - Если
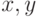 и
и  представимы в виде
представимы в виде 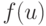 или
или 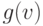 , то в этом случае матрицы
, то в этом случае матрицы  и
и  следует записывать в виде
следует записывать в виде  или
или  соответственно.
соответственно.
Рассмотрим несколько задач построения графиков поверхностей заданных параметрически.
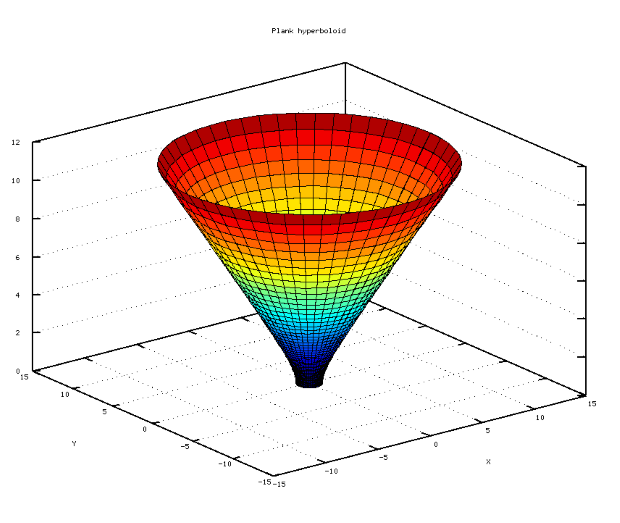
Пример 4.17. Построить поверхность однополостного гиперболоида, уравнение которого задано в параметрическом виде ![x(u, v) = ch(u)cos(v), y (u, v) = ch(u)sin(v), z (u, v) = sh(u), u \in [0, \pi ], v \in [0, 2\pi]](/sites/default/files/tex_cache/f55b440c5f86862406cc7bbd4b84a546.png) .
.
В листинге 4.18 представлено решение этой задачи, согласно описанному выше алгоритму. График однополостного гиперболоида представлен на рис. 4.22.
clear all; h =3.14/50; u = [0:h:3.14]’; % Формируем вектор-столбец u. % Формируем вектор-строку v. Обратите внимание, u — столбец, % v — строка с одинаковым количеством элементов. v =[0:2*h:6.28]; % Формируем матрицу X как матричное произведение ch(u) cos(v). X=cosh(u)*cos(v); % Формируем матрицу Y как матричное произведение ch(u)*sin(v). Y=cosh(u)*sin(v); % Формируем матрицу Z как матричное произведение столбца sh(u) % на строку ones(size(v)). Z=sinh(u)*ones(size(v)); % Формируем график поверхности. surf(X, Y, Z); grid on; % Подписываем график и оси. title(’Plank hyperboloid’); xlabel(’X’); ylabel(’Y’); zlabel(’Z’)Листинг 4.18. Построение поверхности гиперболоида (пример 4.17).
Рассмотрим несколько способов построения сферы в Octave.
Пример 4.18. Построить поверхность сферы с центром  и радиусом
и радиусом  .
.
В декартовой системе координат уравнение сферы имеет вид: 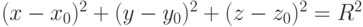 . Его можно записать в параметрическом виде
. Его можно записать в параметрическом виде
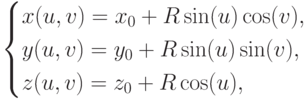
где ![u\in[0,2\pi), v\in[0,\pi]](/sites/default/files/tex_cache/a497fbd91188da7e3fa2c8328f3da4fa.png) .
.
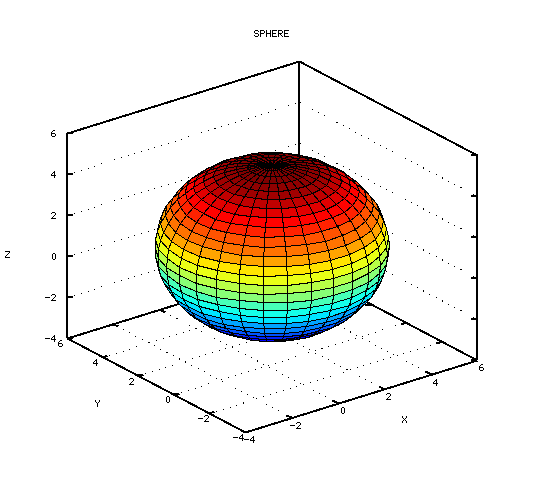
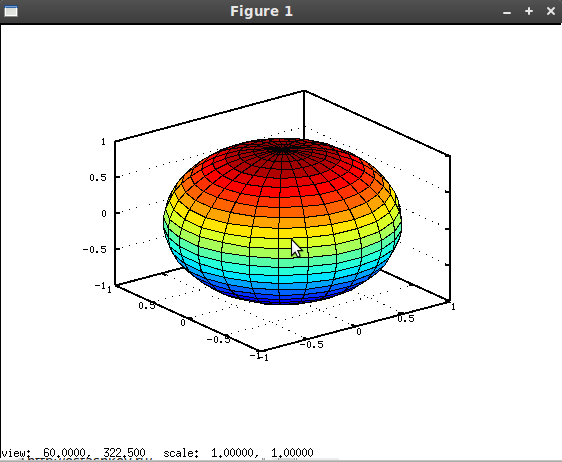
Методика построения сферы подобна методике построения однополостного гиперболоида, описанной в примере 4.17. В листинге 4.19 представлен текст программы построения сферы с центром в точке (1, 1, 1) и радиусом  , а на рис. 4.23 изображена сфера.
, а на рис. 4.23 изображена сфера.
clear all; h=pi/30; u=[-0:h:pi]’; % Формируем вектор-столбец u. v =[0:2*h:2*pi ]; % Формируем вектор-строку v. % Формируем матрицу X, используя матричное произведение sin(u)*cos(v). x=1+4*sin(u)*cos(v); % Формируем матрицу Y, используя произведение sin(u)*sin(v). y=1+4*sin(u)*sin(v); % Формируем матрицу Z, используя произведение столбца % cos(u) на строку ones(size(v)). z=1+4*cos(u)*ones(size(v)); % Формируем график поверхности. surf(x, y, z); grid on; % Подписываем график и оси. title(’SPHERE’); xlabel(’X’); ylabel(’Y’); zlabel(’Z’);Листинг 4.19. Построение сферы (пример 4.18).
Octave содержит встроенную функцию ![[X, Y, Z] = sphere(n)](/sites/default/files/tex_cache/c70e45dc52aa66b7020ab38e9f9ed185.png) , позволяющую формировать матрицы
, позволяющую формировать матрицы 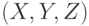 размерности
размерности  для построения сферы единичного радиуса (см. пример 4.18) с центром в начале координат.
для построения сферы единичного радиуса (см. пример 4.18) с центром в начале координат.
Для построения сферы единичного радиуса с центром в начале координат достаточно двух команд ![[X,Y,Z]=sphere(n); surf(X,Y,Z)](/sites/default/files/tex_cache/3457bf40b11aa7f14a7915af6e062518.png) . Чем n больше, тем более "округлой" будет сфера. На рис. 4.24 изображена
сфера единичного радиуса в центре в начале координат при n = 25.
. Чем n больше, тем более "округлой" будет сфера. На рис. 4.24 изображена
сфера единичного радиуса в центре в начале координат при n = 25.
Встроенную функцию  можно использовать и для построения сферы с центром
можно использовать и для построения сферы с центром  и радиусом
и радиусом  . В листинге 4.20 приведено решение примера 4.18 с помощью функции sphere(n).
. В листинге 4.20 приведено решение примера 4.18 с помощью функции sphere(n).
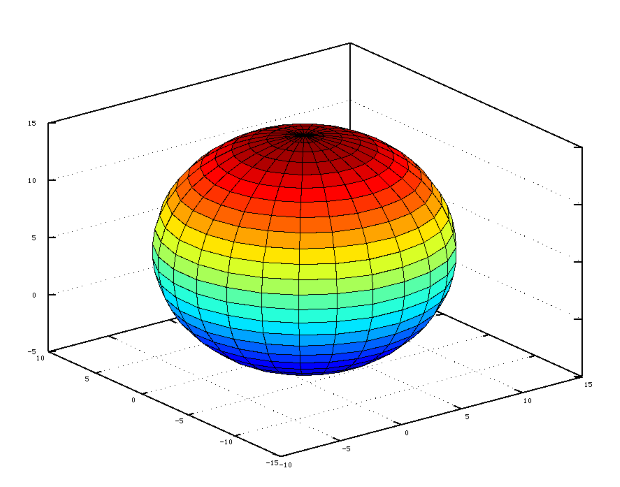
clear all; x0 =2; y0=_2;z0 =5;R=10 % Определяем центр и радиус сферы. % Формируем матрицы X, Y, Z для построения сферы единичного радиуса % с центром в начале координат, используя функцию sphere(n). [X, Y, Z]= sphere(25); % Пересчитываем матрицы X,Y,Z для сферы с центром x0, y0, z0 и радиусом R. X=x0+R*X;Y=y0+R*Y; Z=z0+R*Z; surf(X, Y, Z) % Изображаем сферуЛистинг 4.20. Построение сферы с помощью sphere (пример 4.18).
В результате работы программы будет построена сфера, представленная на рис. 4.25.
Сфера является частным случаем более общей фигуры — эллипсоида. Рассмотрим два способа построения эллипсоида.
увеличить изображение
Рис. 4.25. Сфера, построенная с помощью программы, представленной в листинге 4.20
Пример 4.19. Построить поверхность эллипсоида, уравнение которой задано в параметрическом виде:
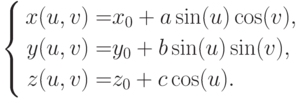
Здесь 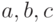 — полуоси эллипсоида,
— полуоси эллипсоида,  — центр эллипсоида.
— центр эллипсоида.
Методика построения эллипсоида подобна тому, как ранее были построены однополостный гиперболоид (пример 4.17) и сфера (пример 4.18). Для этого необходимо сформировать матрицы  и
и  , после чего вызвать функцию
, после чего вызвать функцию 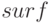 . Как это сделать показано в листинге 4.21.
. Как это сделать показано в листинге 4.21.
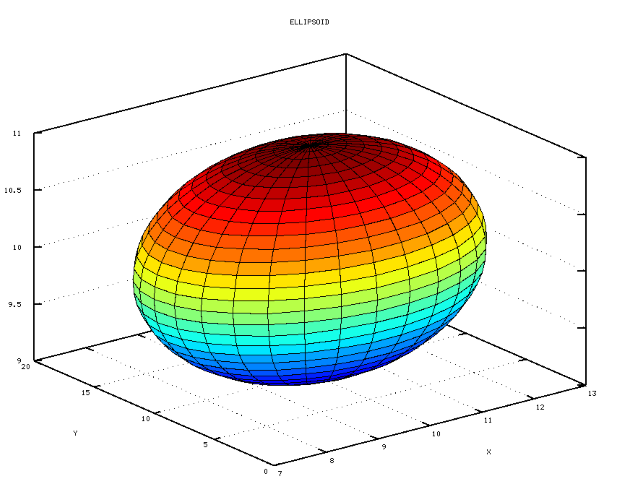
clear all; h=pi/30; u=[-0:h:pi]’; % Формируем вектор-столбец u. v =[0:2*h:2*pi]; % Формируем вектор-строку v. % Формируем матрицу X, используя матричное произведение sin(u)*cos(v). a =3;b=7; c =1; x0=y0=z0 =10;x=x0+a*sin(u)*cos(v); % Формируем матрицу Y, используя произведение sin(u)*sin(v). y=y0+b*sin(u)*sin(v); % Формируем матрицу Z, используя произведение столбца % cos(u) на строку ones(size(v)). z=z0+c*cos(u)*ones(size(v)); surf(x, y, z); grid on; % Формируем эллипсоид. % Подписываем график и оси. title(’ELLIPSOID’); xlabel(’X’); ylabel(’Y’); zlabel(’Z’);Листинг 4.21. Построение поверхности эллипсоида (пример 4.19).
Эллипсоид с центром в точке (10, 10, 10) и полуосями  представлен на рис. 4.26.
представлен на рис. 4.26.
Однако, для построения эллипсоида в Octave существует функция ![[X, Y, Z] = ellipsoid(xc, yc, zc, xr, yr, zr, n)](/sites/default/files/tex_cache/7885bf6efc747548205123d09ad4cdb2.png) , которая позволяет автоматически сформировать матрицы
, которая позволяет автоматически сформировать матрицы 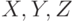 .
.
В функции  :
:
- —
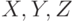 — формируемые для построения поверхности матрицы размерности n + 1;
— формируемые для построения поверхности матрицы размерности n + 1; - —
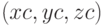 — координаты центра эллипсоида;
— координаты центра эллипсоида; - —
 — полуоси эллипсоида.
— полуоси эллипсоида.
Для построения эллипсоида, представленного на рис. 4.23 достаточно ввести команды
a =3;b=7; c =1; x0=y0=z0 =10; [X, Y, Z]= ellipsoid(x0, y0, z0, a, b, c, 30); surf(x, y, z); grid on; title(’ELLIPSOID’); xlabel(’X’); ylabel(’Y’); zlabel(’Z’);
Для построения цилиндров и круговых конусов можно использовать функцию  для формирования матриц
для формирования матриц 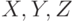 . Затем строим саму поверхность (цилиндр, конус) с помощью функции
. Затем строим саму поверхность (цилиндр, конус) с помощью функции 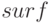 .
.
Познакомимся с функцией cylinder подробнее. Обращение к функции имеет вид. ![[X, Y, Z] = cylinder(r, n)](/sites/default/files/tex_cache/242c622256b9b722a04b89880882223a.png) ;
;
Здесь  — массив радиусов; если мы строим цилиндр,
— массив радиусов; если мы строим цилиндр,  — массив, состоящий из двух одинаковых значений, функция требует как минимум два значения, и для построения цилиндра это будут радиус верхнего и нижнего основания; при построении конуса r является массивом радиусов горизонтальных сечений кругового конуса;
— массив, состоящий из двух одинаковых значений, функция требует как минимум два значения, и для построения цилиндра это будут радиус верхнего и нижнего основания; при построении конуса r является массивом радиусов горизонтальных сечений кругового конуса;
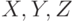 — формируемые для построения поверхности (конуса, цилиндра) матрицы размерности
— формируемые для построения поверхности (конуса, цилиндра) матрицы размерности  .
.
Рассмотрим несколько примеров.
Пример 4.20. Построить цилиндр радиуса  и высотой
и высотой 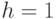 .
.
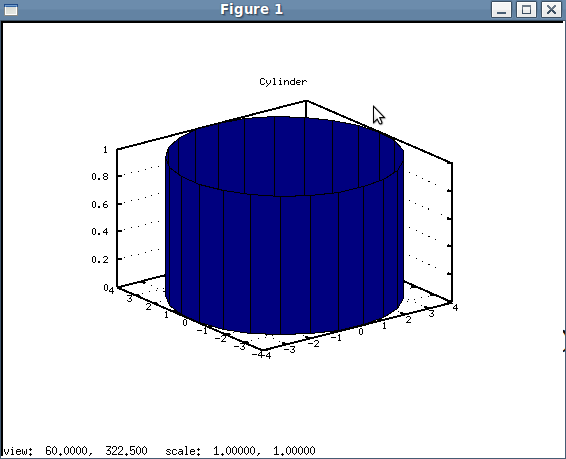
Текст программы приведён в листинге 4.22, график — на рисунке 4.27.
увеличить изображение
Рис. 4.26. Эллипсоид с центром в точке (10, 10, 10) и полуосями a = 3,b = 7, c = 1
clear all;
[x, y, z] = cylinder([4, 4], 25); % Формирование матриц x, y, z.
grid on; surf(x, y, z); % Построение цилиндра.
title("Cylinder")
Листинг
4.22.
Построение цилиндра высотой 1 (пример 4.20).
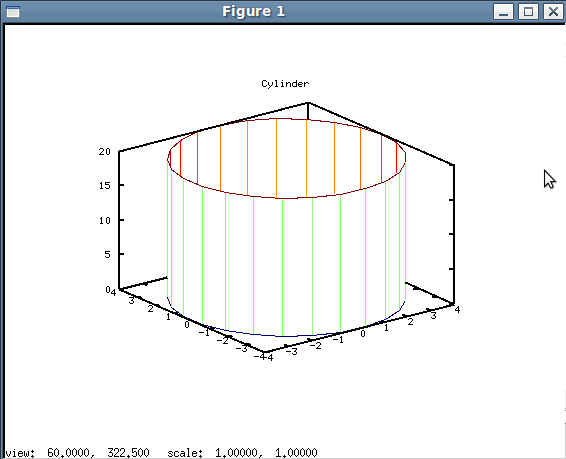
Пример 4.21. Построить цилиндр радиуса 4 и высотой 20.
Текст программы приведён в листинге 4.23, график — на рисунке 4.28.
clear all;
[x, y, z] = cylinder([4, 4], 25); % Формирование матриц x, y, z.
grid on;
surf(x, y, 20*z ); % Построение цилиндра с учётом высоты h = 20.
title("Cylinder")
Листинг
4.23.
Построение цилиндра высотой 20 (пример 4.21).
Пример 4.22. Примеры круговых конусов.
Рассмотрим несколько примеров.
Усечённый круговой конус, представленный на рис. 4.29, генерируется программой из листинга 4.24.
clear all; [x, y, z] = cylinder(2:1:10, 25);
grid on; surf(x, y, z);
title("Cone"); xlabel(’X’); ylabel(’Y’); zlabel(’Z’);
Листинг
4.24.
Построение усечённого кругового конуса (пример 4.22).
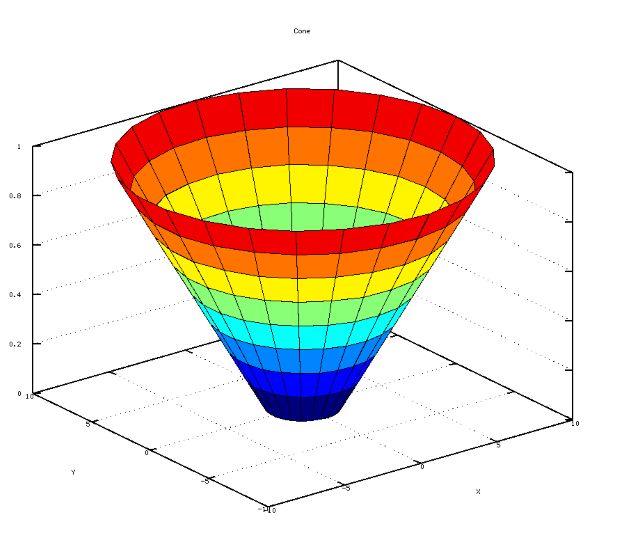
Круговой конус, представленный на рис. 4.30, генерируется программой в листинге 4.25.
clear all[x, y, z] = cylinder([5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5], 25);
grid on; mesh(x, y, z);
title("Cone") xlabel(’X’); ylabel(’Y’); zlabel(’Z’);
Листинг
4.25.
Построение кругового конуса (пример 4.22).
В завершении приведён листинг 4.26, который генерирует поверхность, представленную на рис. 4.31.
clear all[x, y, z] = cylinder([1, 3, 5, 7, 6, 4], 25);
surf(x, y, z);
title("Surface"); xlabel(’X’); ylabel(’Y’); zlabel(’Z’);
Листинг
4.26.
Поверхность (см. рис. 4.30)