|
Возможна ли разработка приложения на Octave с GUI? |
Построение графиков
4.4.5 Примеры
Пример 4.23. Написать программу создания графиков функций  на интервале [-5;5]. Графики функций
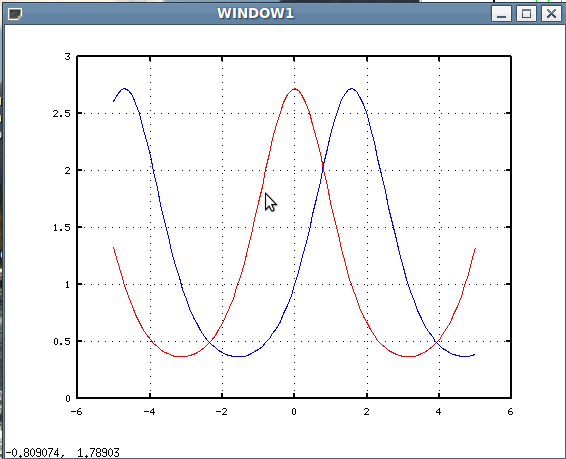
на интервале [-5;5]. Графики функций 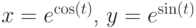 изобразить в графическом окне с именем WINDOW1 красным и синим цветом, а график функции
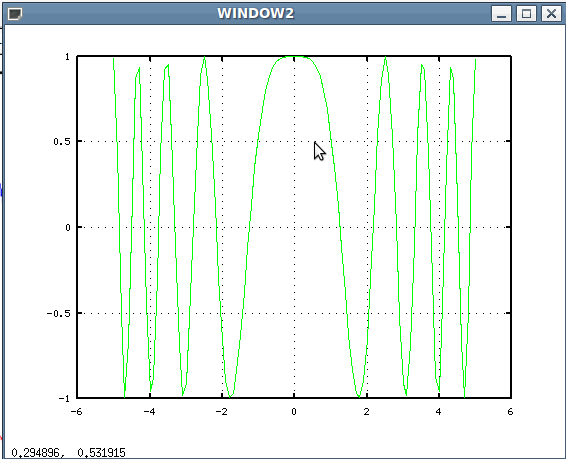
изобразить в графическом окне с именем WINDOW1 красным и синим цветом, а график функции  — в окне с именем WINDOW2 зелёным. В обоих окнах вывести линии сетки.
— в окне с именем WINDOW2 зелёным. В обоих окнах вывести линии сетки.
В листинге 4.29 приведено решение этой задачи с подробными комментариями.
t = -5:0.1:5; x= exp(cos(t)); y= exp(sin(t)); z=cos(t.^2); % Создаём первое графическое окно, указатель, на которое будет hfig1=figure; % храниться в переменной hfig1. % Создаём второе графическое окно, указатель, на которое будет hfig2=figure; % храниться в переменной hfig2. figure(hfig1); % Объявляем первое графическое окно текущим. % Выводим в нём оси, указатель на на которые будет храниться hAxes1=axes; % в переменной hAxes1. % Выводим в этом окне график функций x(t) и y(t), указатель на который % записываем в переменную h_gr1. В h_gr(1) будет храниться первая % линия — x(t), в h_gr(2) будет храниться вторая линия — y(t). h_gr1=plot(t, x, t, y); figure(hfig2); % Объявляем второе графическое окно текущим. % Выводим в нём оси, указатель на на которые будет храниться hAxes2=axes; % в переменной hAxes2. % Выводим в этом окне график функции z(t), указатель на который h_gr2=plot(t, z); % записываем в переменную h_gr2 . figure(hfig1); % Объявляем первое графическое окно текущим % Далее устанавливаем свойства осей и графиков в первом окне. % Отказываемся от стандартной нумерации окон для первого окна. set(hfig1, ’numbertitle’, ’off’); % Устанавливаем новое имя первого графического окна. set(hfig1, ’name’, ’WINDOW1’); % Включаем отображение линий сетки, перпендикулярной оси ОХ % для осей hAxes1. set(hAxes1, ’xgrid’, ’on’); % Включаем отображение линий сетки, перпендикулярной оси ОY set(hAxes1, ’ygrid’, ’on’); % для осей hAxes1. % Устанавливаем красный цвет первой линии в первом графическом окне. set(h_gr1(1), ’color’, ’r’); % Устанавливаем синий цвет второй линии в первом графическом окне. set(h_gr1(2), ’color’, ’b’); figure(hfig2);% Объявляем второе графическое окно текущим % Далее устанавливаем свойства осей и графиков во втором окне. % Отказываемся от стандартной нумерации окон для второго окна. set(hfig2, ’numbertitle’, ’off’); % Устанавливаем новое имя второго графического окна. set(hfig2, ’name’, ’WINDOW2’); % Включаем отображение линий сетки, перпендикулярной оси ОХ set(hAxes2, ’xgrid’, ’on’); % для осей hAxes2. % Включаем отображение линий сетки, перпендикулярной оси ОY set(hAxes2, ’ygrid’, ’on’); % для осей hAxes2. % Устанавливаем зелёный цвет первой линии во втором графическом окне. set(h_gr2, ’color’, ’g’); % Эта функция может быть и такой: set(h_gr2(1), ’ Color ’, ’ g ’);Листинг 4.29. Программа создания графиков (пример 4.23).
На рис. 4.39 и 4.40 представлены созданные с помощью программы, приведённой в листинге 4.29, окна с графиками функций 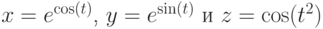 соответственно.
соответственно.
При программировании работы с графическими окнами вызов функции 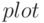 может осуществляться со всеми параметрами, рассмотренными в этой главе. Для того, чтобы добавить новый график в текущие оси, необходимо перед вызовом функции
может осуществляться со всеми параметрами, рассмотренными в этой главе. Для того, чтобы добавить новый график в текущие оси, необходимо перед вызовом функции 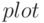 выполнить команду
выполнить команду 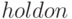 . При добавлении графика в текущие оси с помощью функции
. При добавлении графика в текущие оси с помощью функции 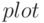 необходимо самостоятельно устанавливать цвет и тип графика.
необходимо самостоятельно устанавливать цвет и тип графика.
На рис. 4.39. изображены графики функций: 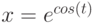 и
и 
На рис. 4.40. изображен график функции: 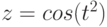
Пример 4.24. Изобразить графики функций 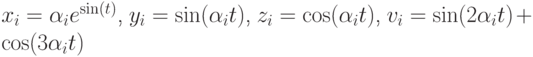 на интервале [-5; 5], если коэффициенты
на интервале [-5; 5], если коэффициенты 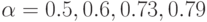 хранятся в текстовом файле gr.txt.
хранятся в текстовом файле gr.txt.
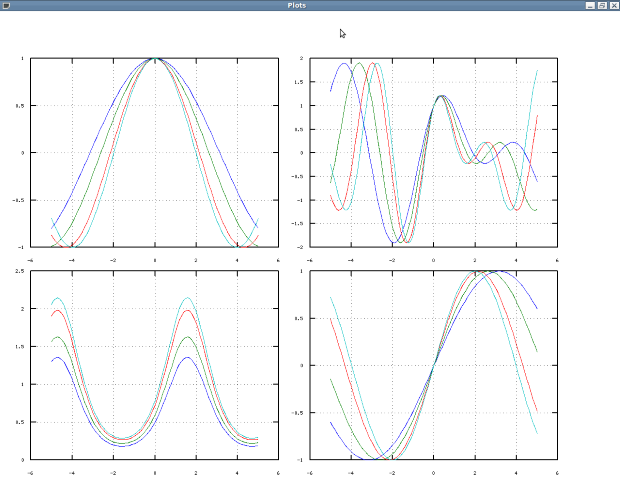
При решении этой задачи необходимо будет построить четыре множества графиков  . Каждое множество будем изображать в своих осях. В листинге 4.30 приведена программа, а на рис. 4.41 представлено полученное в результате графическое окно.
. Каждое множество будем изображать в своих осях. В листинге 4.30 приведена программа, а на рис. 4.41 представлено полученное в результате графическое окно.
f=fopen(’gr.txt’, ’rt’); % Открываем файл gr.txt в режиме чтения. alf=fscanf(f, ’%f’, 4); % Считываем из него данные в массив alf. % Формируем массивы t, x, y, z, v t = -5:0.1:5; x=alf*exp(sin(t)); y=sin(alf*t); z=cos(alf*t); v=sin(2*alf*t)+cos(3*alf*t); hfig1=figure; % Создаём графическое окно % Устанавливаем новое имя первого графического окна. set(hfig1, ’numbertitle’, ’off’); set(hfig1, ’name’, ’Plots’); % Выводим в нём оси, указатель на которые будет храниться в переменной % haxes1. Оси будут располагаться в левом нижнем углу графического окна. haxes1=axes(’position’, [0.05 0.05 0.4 0.4]); plot(t, x); % Выводим множество графиков xi(t) % Выводим линии сетки на осях. set(haxes1, ’xgrid’, ’on’, ’ygrid’, ’on’); % Выводим в графическом окне оси, указатель на которые будет храниться % в переменной haxes2. Оси будут располагаться в правом нижнем углу % графического окна. haxes2=axes(’position’, [0.5 0.05 0.4 0.4]); plot(t, y); % Выводим множество графиков yi(t). % Выводим линии сетки на осях. set(haxes2, ’xgrid’, ’on’, ’ygrid’, ’on’); % Выводим в графическом окне оси, указатель на которые будет % храниться в переменной haxes3. Оси будут располагаться в % левом верхнем углу графического окна. haxes3=axes(’position’, [0.05 0.5 0.4 0.4]); plot(t, z); % Выводим множество графиков zi(t) % Выводим линии сетки на осях. set(haxes3, ’xgrid’, ’on’, ’ygrid’, ’on’); % Выводим в графическом окне оси, указатель на которые будет % храниться в переменной haxes3. Оси будут располагаться в % правом верхнем углу графического окна. haxes4=axes(’position’, [0.5 0.5 0.4 0.4]); plot(t, v); % Выводим множество графиков vi(t). % Выводим линии сетки на осях. set(haxes4, ’xgrid’, ’on’, ’ygrid’, ’on’);Листинг 4.30. Построение графиков функций (пример 4.24).
На графиках не хватает текстовой информации, которая бы поясняла выведенные графики.
Для вывода текста можно использовать следующие функции:
-
 предназначена для вывода заголовка графика;
предназначена для вывода заголовка графика; -
 служит для вывода текста под осью
служит для вывода текста под осью ;
; -
 предназначена для вывода названия оси
предназначена для вывода названия оси 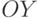 ;
; -
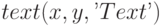 служит для вывода текста в точке с координатами
служит для вывода текста в точке с координатами  ; координаты
; координаты  задаются в системе координат графика, нет необходимости пересчитывать их в "экранную" систему координат.
задаются в системе координат графика, нет необходимости пересчитывать их в "экранную" систему координат.
На рис. 4.41. изображены графики функций: 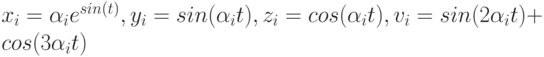
В листинге 4.31 представлена программа построения графика  на интервале
на интервале ![[-2\pi, 2\pi]](/sites/default/files/tex_cache/d677f23549479b8742616a37ddcd07b0.png) вместе с заголовками, подписями осей и примером использования функции
вместе с заголовками, подписями осей и примером использования функции 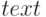 . Полученный в результате работы программы график представлен на рис. 4.42.
. Полученный в результате работы программы график представлен на рис. 4.42.
t=-2*pi:pi/50:2*pi; x=sin(t); plot(t, x); xlabel(’t’); ylabel(’x’); title(’Plot function x=sin(t)’); text(-1, -0.8, ’<- Point(-1,-0.8)’);Листинг 4.31. Построение графика синуса с подписями
Все рассмотренные функции вывода текста формирует указатель на созданный текстовый объект, у которого с помощью функции 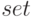 можно установить соответствующие свойства, наиболее часто встречающиеся из которых приведены ниже:
можно установить соответствующие свойства, наиболее часто встречающиеся из которых приведены ниже:
-
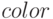 — определяет цвет шрифта;
— определяет цвет шрифта; -
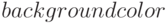 — позволяет определить цвет фона;
— позволяет определить цвет фона; -
 — позволяет установить наклон шрифта;
— позволяет установить наклон шрифта; -
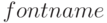 — определяет название шрифта;
— определяет название шрифта; -
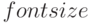 — определяет размер шрифта в пунктах;
— определяет размер шрифта в пунктах; -
 — определяет толщину шрифта;
— определяет толщину шрифта; -
 — позволяет изменять стиль прямоугольной рамки;
— позволяет изменять стиль прямоугольной рамки; -
 — определяет толщину линий прямоугольной рамки.
— определяет толщину линий прямоугольной рамки.
На этом мы заканчиваем краткое знакомство с графическими объектами языка Octave и предлагаем читателю самостоятельно поэкспериментировать с описанными свойствами графических объектов при написании собственных программ.