НОУ ИНТУИТ | Введение в Octave. Лекция 7: Нелинейные уравнения и системы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

7.3 Решение систем нелинейных уравнений

Напомним, что если заданы уравнений с неизвестными и требуется найти последовательность из чисел, которые одновременно удовлетворяют каждому из уравнений, то говорят о системе уравнений.

Несложную систему элементарной подстановкой можно привести к нелинейному уравнению. Рассмотрим несколько примеров, в которых описан такой приём решения нелинейной системы.

Пример 7.16. Решить систему уравнений:

$\left\{\begin{aligned}{(x^2+2y^2=1\\x-y=1.\end{aligned}$

Найдём графическое решение с помощью команд листинга 7.17. На рис. 7.4 видно, что система имеет два решения.

	
% Верхняя часть эллипса
function y=f1(x)
	y=sqrt((1-x.^2)/2);
end;
% Нижняя часть эллипса
function y=f2(x)
	y= -sqrt((1-x.^2)/2);
end;
% Прямая
function y=f3(x)
	y=x-1;
end;
% Построение графика
cla; okno1=figure();
x1 = -1:0.01:1; x2 = -1.5:0.1:1.5;
L1=plot(x1, f1(x1), x1, f2(x1));
set(L1, ’LineWidth’, 2, ’Color’, ’k’)
hold on
L2=plot(x2, f3(x2));
set(L2, ’LineWidth’, 3, ’Color’, ’k’)
set(gca, ’xlim’, [-1.5, 1.5]); set(gca, ’ylim’, [-1, 1]);
set(gca, ’xtick’, [-1.5:0.2:1.5]); set(gca, ’ytick’,[- 1:0.2:1]);
grid on; xlabel(’x’); ylabel (’y’);

Листинг 7.17. Построение графика системы уравнений (пример 7.16).

Рис. 7.4. Решение системы нелинейных уравнений из примера 7.16

Не сложно убедиться, что данная система легко сводится к одному уравнению:

$\{y=x-1,x^2+2y^2=1\} \Rightarrow x^2+2(x-1)^2-1=0 \Rightarrow 3x^2-4x+1=0$

.

Решив это уравнение с помощью функции roots , найдём значения . Затем подставим их в одно из уравнений системы, например во второе, и тем самым вычислим значения :

	
>>> p=[3 -4 1];
>>> x=roots(p)
x =
	1.00000
	0.33333
>>> y=x-1
y =
	-1.1102e-16
	-6.6667e-01

Рис. 7.5. Графическое решение примера 7.16

Понятно, что система имеет два решения 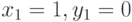x_1=1,y_1=0 и $x_2=\frac{1}{3},y_2=-\frac{2}{3}$ (рис. 7.4). Графическое решение уравнения (листинг 7.18), к которому сводится система, показано на рис. 7.5.

	
function y=f(x)
	y=3-x.^2-4-x+1;
end;
cla; okno1=figure();
x = 0:0.01:1.5;
L=plot(x, f(x)); set(L, ’LineWidth’, 2, ’Color’, ’k’)
set(gca, ’xlim’, [0, 1.5]); set(gca, ’ylim’, [-0.5, 1]);
set(gca, ’xtick’, [0:0.1:1.5]); set(gca, ’ytick’, [-0.5:0.1:1]);
grid on; xlabel(’x’); ylabel(’y’);

Листинг 7.18. График упрощённой системы (пример 7.16).

Дальше >>

Авторизоваться

Введение в Octave

Нелинейные уравнения и системы

7.3 Решение систем нелинейных уравнений

Вопросы и ответы