Нелинейные уравнения и системы

Пример 7.17. Решить систему уравнений:

Проведём элементарные алгебраические преобразования и представим систему в виде одного уравнения: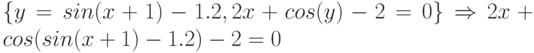

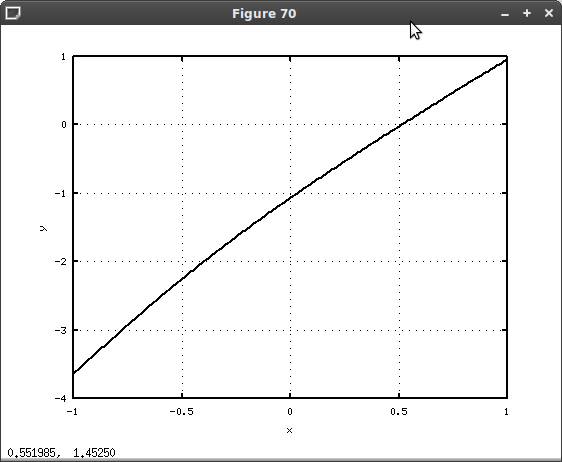
Рис. 7.6 содержит графическое решение уравнения (листинг 7.19), к которому сводится система, его удобно использовать для выбора начального приближения функции . Вторая часть листинга 7.19 содержит решение заданной системы. Здесь значения вычисляется при помощи функции , а значение y определяется из первого уравнения системы.

Рис. 7.6. Графическое решение примера 7.17

	
% Строим график
function y=fun(x)
	z=sin(x+1)-1.2;
	y=2-x+cos(z)-2;
end;
cla; okno1=figure();
x = -1:0.01:1;
L=plot(x, fun(x)); set(L, ’LineWidth’, 2, ’Color’, ’k’)
grid on; xlabel(’x’); ylabel(’y’);
% Находим аналитическое решение системы вблизи x = 0
>>> X=fzero(’fun’, 0)
>>> Y=sin(X+1)-1.2
X = 0.51015
Y = -0.20184

Решить систему нелинейных уравнений, или одно нелинейное уравнение, в Octave можно с помощью функции 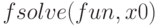, где 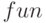— имя функции, которая определяет левую часть уравнения 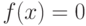или системы уравнений 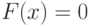(она должна принимать на входе вектор аргументов и возвращать вектор значений), 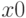— вектор приближений, относительно которого будет осуществляться поиск решения.

Пример 7.18. Найти решение системы нелинейных уравнений:

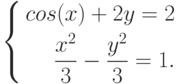
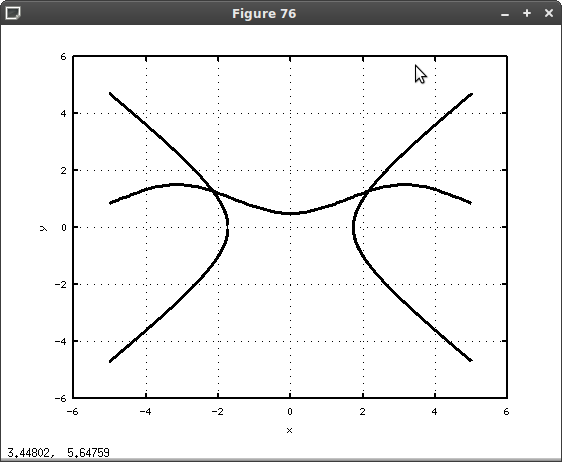
Решим систему графически, для чего выполним перечень команд указанных в листинге 7.20. Результат работы этих команд показан на рис. 7.7. Понятно, что система имеет два корня.

	
% Уравнения, описывающие линии гиперболы
function y=f1(x)
	y=sqrt(x.^2_3);
end;
function y=f2(x)
	y=_sqrt(x.^2_3);
end;
% Уравнение косинусоиды
function y=f3(x)
	y=1_cos(x)/2;
end;
% Построение графика
cla; okno1=figure();
x1 = _5:0.001:_sqrt(3);
x2=sqrt(3):0.001:5;
x3 = _5:0.1:5;
% Гипербола
L1=plot(x1, f1(x1), x1, f2(x1), x2, f1(x2), x2, f2(x2));
set(L1, ’LineWidth’, 3, ’Color’, ’k’)
hold on
% Косинусоида
L2=plot(x3, f3(x3)); set(L2, ’LineWidth’, 3, ’Color’, ’k’)
grid on; xlabel(’x’); ylabel(’y’);

Составим функцию, соответствующую левой части системы. Здесь важно помнить, что все уравнения должны иметь вид 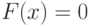. Кроме того, обратите внимание, что и в этой функции — векторы ( — вектор неизвестных, — вектор решений).

	
function[y]= fun(x)
	y(1)=cos(x(1))+2-x(2)-2;
	y(2)=x(1)^2/3-x(2)^2/3-1;
end;

Теперь решим систему, указав в качестве начального приближения сначала вектор [-3, -1], затем [1, 3].

Рис. 7.7. Графическое решение примера 7.18

	
>>> [X1_Y1]= fsolve(’fun’, [-3 -1])
X1_Y1 = -2.1499  1.2736
>>> [X2-Y2]= fsolve(’fun’, [1 3])
X2_Y2 = 2.1499  1.2736

Понятно, что решением примера являются пары 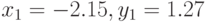и 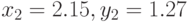, что соответствует графическому решению (рис. 7.7).

Если функция решения нелинейных уравнений и систем имеет вид , то здесь — вектор решений системы, — вектор значений уравнений системы для найденного значения 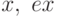— признак завершения алгоритма решения нелинейной системы, отрицательное значение параметра ex означает, что решение не найдено, ноль — досрочное прерывание вычислительного процесса при достижении максимально допустимого числа итераций, положительное значение подтверждает, что решение найдено с заданной точностью.

Пример 7.19. Решить систему нелинейных уравнений:

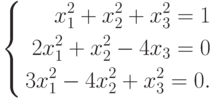
Листинг 7.21 содержит функцию заданной системы и её решение. Обратите внимание на выходные параметры функции . В нашем случае значения функции для найденного решения близки к нулю и признак завершения 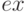положительный, значит, найдено верное решение.

Рис. 7.8. Графическое решение примера 7.20

	
function f=Y(x)
	f(1)=x(1)^2+x(2)^2+x(3)^2-1;
	f(2)=2-x(1)^2+x(2)^2-4-x(3);
	f(3)=3-x(1)^2-4-x(2)+x(3)^2;
end
>>> [x, f, ex]= fsolve(’Y’, [0.5 0.5 0.5] )
x = 0.78520  0.49661  0.36992
f = 1.7571e-08  3.5199e-08  5.2791e-08
ex = 1

Пример 7.20. Решить систему:

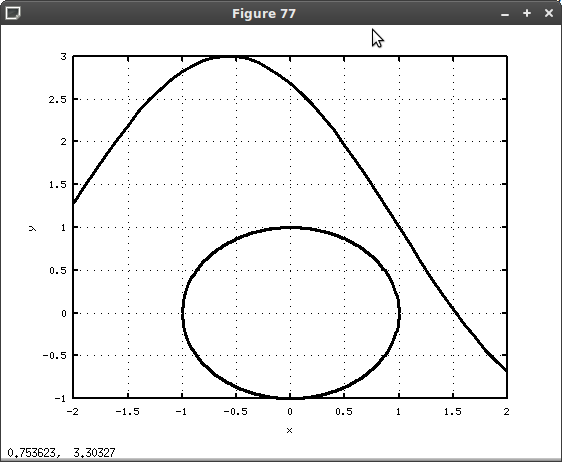
Графическое решение системы (рис. 7.8) показало, что она корней не имеет. Рисунок был получен с помощью команд листинга 7.22.

	
% Уравнения линий окружности
function y=f1(x)
	y=sqrt(1-x.^2);
end;
function y=f2(x)
	y= -sqrt(1-x.^2);
end;
% Уравнение синусоиды
function y=f3(x)
	y=1-2-sin(x-1);
end;
okno1=figure(); cla;
x1 = -1:0.01:1; x3 = -2:0.1:2;
% Окружность
L1=plot(x1, f1(x1), x1, f2(x1)); set(L1, ’LineWidth’, 3, ’Color’, ’k’)
hold on
% Синусоида
L2=plot(x3, f3(x3)); set(L2, ’LineWidth’, 3, ’Color’, ’k’)
grid on; xlabel(’x’); ylabel(’y’);

Однако применение к системе функции даёт положительный ответ, что видно из листинга 7.23. Происходит это потому, что алгоритм, реализованный в этой функции, основан на минимизации суммы квадратов компонент вектор–функции. Следовательно, функция в этом случае нашла точку минимума, а наличие точки минимума не гарантирует существование корней системы в её окрестности.

	
function[y]= fun(x)
	y(1)=x(1)^2+x(2)^2-1;
	y(2)=2-sin(x(1)-1)+x(2)-1;
end;
>>> [ X1_Y1]= fsolve(’fun’, [1 1])
X1_Y1 = 1.04584  0.52342