|
Возможна ли разработка приложения на Octave с GUI? |
Нелинейные уравнения и системы
Пример 7.4. Разложить выражение 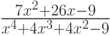 на простейшие дроби.
на простейшие дроби.
Из листинга 7.4 видно, что значения векторов  и
и  — комплексные числа, то есть, на первый взгляд кажется, что выражение невозможно разложить на простейшие рациональные дроби. Однако задача имеет решение:
— комплексные числа, то есть, на первый взгляд кажется, что выражение невозможно разложить на простейшие рациональные дроби. Однако задача имеет решение:
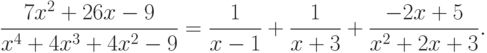
>Выражение 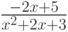 — простейшая дробь вида
— простейшая дробь вида  . Здесь знаменатель невозможно разложить на простые рациональные множители первой степени. Таким образом, функция
. Здесь знаменатель невозможно разложить на простые рациональные множители первой степени. Таким образом, функция  выполняет разложение только на простейшие дроби вида
выполняет разложение только на простейшие дроби вида 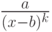 .
.
>>> p1=[1 26 -9]; >>> p2=[1 4 4 -9]; >>> [a, b, c, k]= residue(p1, p2) a = -0.100000 - 6.120680i -0.100000 + 6.120680i 1.200000 + 0.000000i b = -2.50000 + 1.65831i -2.50000 - 1.65831i 1.00000 + 0.00000i c = [ ] (0x0) k = 1 1 1Листинг 7.4. Неудача в разложении на дроби (пример 7.4).
Вычислить значение многочлена в заданной точке можно с помощью функции 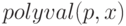 , где
, где  — многочлен степени
— многочлен степени 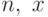 — значение, которое нужно подставить в многочлен.
— значение, которое нужно подставить в многочлен.
Пример 7.5. Вычислить значение многочлена  в точках
в точках 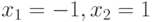 (листинг 7.5).
(листинг 7.5).
>>> p=[1 -1 3 0 -8 1 -10]; >>> x=[-1,1]; >>> polyval(p, x) ans = -14 -14Листинг 7.5. Вычисление значения многочлена (пример 7.5).
Вычислить производную от многочлена позволяет функция  , где
, где  — многочлен степени
— многочлен степени  . Функция формирует вектор коэффициентов многочлена, являющегося производной от
. Функция формирует вектор коэффициентов многочлена, являющегося производной от  .
.
Производную произведения двух векторов вычисляет функция  , где
, где 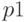 и
и  — многочлены.
— многочлены.
Вызов функции в общем виде ![[q, r] = polyder(p1, p2)](/sites/default/files/tex_cache/2aea1dce1b3dafcbc808f8f3fbafe0d7.png) приведёт к вычислению производной от частного p1 на
приведёт к вычислению производной от частного p1 на  и выдаст результат в виде отношения полиномов
и выдаст результат в виде отношения полиномов  и
и  .
.
Пример 7.6. Вычислить производную от многочлена 
Листинг 7.6 показал, что решением примера является многочлен 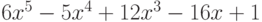 .
.
>>> p=[1 -1 3 0 -8 1 -10]; >>> polyder(p) ans = 6 -5 12 0 -16 1Листинг 7.6. Вычисление производной многочлена (пример 7.6).
