Нелинейные уравнения и системы

Пример 7.7. Вычислить производную от произведения многочленов .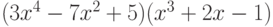

Листинг 7.7 показал, что решением примера является многочлен .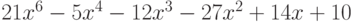

	
>>> p1=[3 0 -7 0 5];
>>> p2=[1 0 2 -1];
>>> polyder(p1, p2)
ans = 21 0 -5 -12 -27 14 10

Пример 7.8. Вычислить производную от выражения

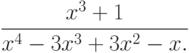
Из листинга 7.8 видно, что решение примера имеет вид

	
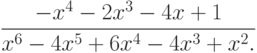
>>> p1=[1 0 0 1];
>>> p2=[1 -3 3 -1 0];
>>> [q, r]= polyder(p1, p2)
q = -1 -2  0  -4  1
r = 1 -4  6  -4  1  0  0

Взять интеграл от многочлена позволяет функция , где — многочлен степени — постоянная интегрирования, значение по умолчанию равно нулю. Функция формирует вектор коэффициентов многочлена, являющегося интегралом от .

Пример 7.9. Найти .

Согласно листингу 7.9 решение имеет вид:

Если определить значение постоянной интегрирования (вторая часть листинга 7.9), то решение будет таким:

	
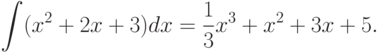
>>> p=[1 2 3];
>>> polyint(p)
ans = 0.33333 1.00000 3.00000 0.00000
% Указываем постоянную интегрирования
>>> polyint(p, 5)
ans = 0.33333 1.00000 3.00000 5.00000

Построить многочлен по заданному вектору его корней позволяет функция 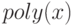, где — вектор корней искомого полинома.