|
Возможна ли разработка приложения на Octave с GUI? |
Нелинейные уравнения и системы
Пример 7.10. Записать алгебраическое уравнение, если известно, что его корни 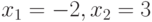 .
.
Согласно листингу 7.10 решение примера имеет вид: 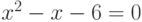
>>> x=[-2 3]; >>> poly(x) ans = 1 -1 -6Листинг 7.10. Построение многочлена по корням (пример 7.10).
Решить алгебраическое уравнение  можно при помощи встроенной функции
можно при помощи встроенной функции  , где
, где  — многочлен степени
— многочлен степени  . Функция формирует вектор, элементы которого являются корнями заданного полинома.
. Функция формирует вектор, элементы которого являются корнями заданного полинома.
Пример 7.11. Решить алгебраическое уравнение 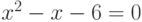 .
.
Из листинга 7.11 видно, что значения 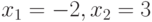 являются решением уравнения.
являются решением уравнения.
>>> p=[1 -1 -6]; >>> roots(p) ans = 3 -2Листинг 7.11. Решение алгебраического уравнения (пример 7.11).
Пример 7.12. Найти корни полинома 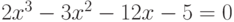 .
.
Найдём корни полинома, так как показано в листинге 7.12.
>>> p=[2 -3 -12 -5]; >>> x=roots(p) x = 3.44949 -1.44949 -0.50000Листинг 7.12. Нахождение корней полинома (пример 7.12).
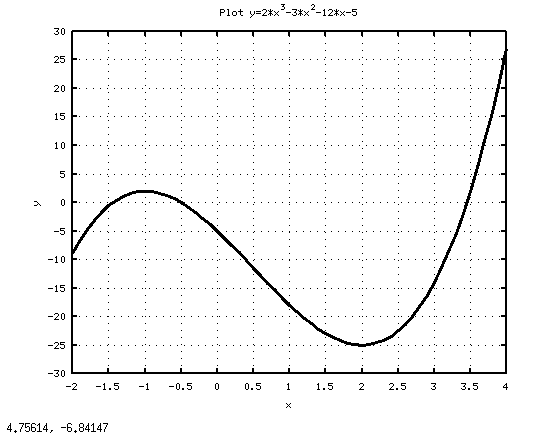
Графическое решение заданного уравнения показано в листинге 7.13 и на рис. 7.1. Точки пересечения графика с осью абсцисс и есть корни уравнения. Не трудно заметить, что графическое решение совпадает с аналитическим (листинг 7.12).
cla; okno1=figure(); x = - 2:0.1:5.5; y=2-x.^3-3-x.^2-12-x-5; pol=plot(x, y); set(pol, ’LineWidth’, 3, ’Color’, ’k’) set(gca, ’xlim’, [-2, 4]); set(gca, ’ylim’, [-30, 30]); set(gca, ’xtick’, [-2:0.5:4]); set(gca, ’ytick’, [-30:5:30]); grid on; xlabel(’x’); ylabel(’y’); title(’Plot y=2*x^3-3*x^2-12*x-5’);Листинг 7.13. Графическое нахождение корней (пример 7.12).
Пример 7.13. Найти решение уравнения 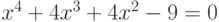 .
.
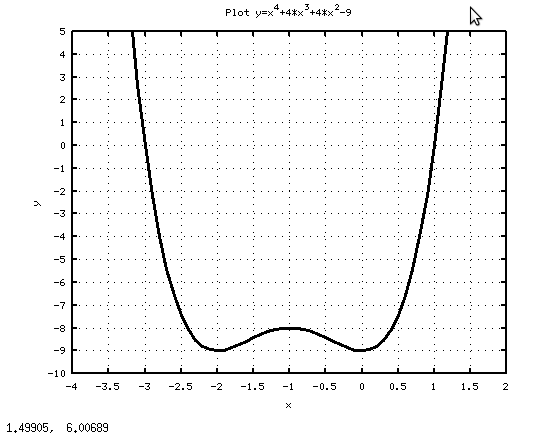
Графическое решение примера было получено при помощи последовательности команд приведённых в первой части листинга 7.14. На рис. 7.2 видно, что заданное алгебраическое уравнение имеет два действительных корня. Аналитическое решение примера, представленное во второй части листинга 7.14 показывает не только действительные, но и комплексные корни.
% Графическое нахождение корней cla; okno1=figure(); x = -4:0.1:2; y=x.^4+4-x.^3+4-x.^2-9; pol=plot(x, y); set(pol, ’LineWidth’, 3, ’Color’, ’k’) set(gca, ’xlim’, [-4, 2]); set(gca, ’ylim’, [-10, 5]); set(gca, ’xtick’, [-4:0.5:2]); set(gca, ’ytick’, [-10:1:5]); grid on; xlabel(’x’); ylabel(’y’); title(’Plot y=x^4+4*x^3+4*x^2-9’); % Аналитическое нахождение корней >>> p=[1 4 4 0 -9]; >>> x=roots(p) x = -3.00000 + 0.00000i -1.00000 + 1.41421i -1.00000 - 1.41421i 1.00000 + 0.00000iЛистинг 7.14. Графическое и аналитическое нахождение корней уравнения (пример 7.13).