НОУ ИНТУИТ | Введение в Octave. Лекция 6: Векторная алгебра и аналитическая геометрия

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

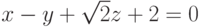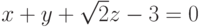Пример 6.19. Найти угол между плоскостями $x-y+\sqrt{2}z+2=0$ и $x+y+\sqrt{2}z-3=0$ .

Решение показано в листинге 6.20.

	
% Исходные данные
N1=[1, -1, sqrt( 2 ) ]; N2=[1,1, sqrt( 2 ) ];
% Угол между плоскостями
fi =acos( dot (N1, N2) /norm(N1) /norm(N2) );
fi_1= round( f i * 180/ pi )
fi_2=180-fi_1
% Решение
fi_1 = 60
fi_2 = 120

Листинг 6.20. Вычисление угла между плоскостями (пример 6.19).

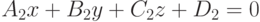Два уравнения A_1x+B_1y+C_1z+D_1=0 и A_2x+B_2y+C_2z+D_2=0 представляют прямую линию, если коэффициенты 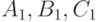A_1, B_1, C_1 не пропорциональны коэффициентам 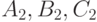A_2, B_2, C_2 (то есть плоскости не параллельны). Если коэффициенты 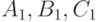пропорциональны коэффициентам 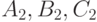, но свободные члены не подчинены той же пропорции 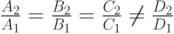$\frac{A_2}{A_1}=\frac{B_2}{B_1}=\frac{C_2}{C_1}\neq \frac{D_2}{D_1}$ , то заданные уравнения не представляют никакого геометрического образа. Если все четыре величины пропорциональны 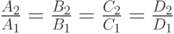$\frac{A_2}{A_1}=\frac{B_2}{B_1}=\frac{C_2}{C_1}=\frac{D_2}{D_1}$ , то заданные уравнения представляют одну и ту же плоскость.

Пример 6.20. Построить прямые линии, заданные уравнениями:

a) 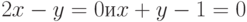2x - y = 0 и x + y - 1 = 0 ;

b) 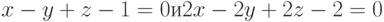x - y + z - 1 = 0 и 2x - 2y + 2z - 2 = 0 ;

c) 2x - 7y + 12z - 4 = 0 и 4x - 14y + 24z - 12 = 0 .

Решение показано в листинге 6.21. Для построения плоскости применялась функция 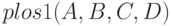plos1(A, B, C, D) , описанная в примере 6.17.

	
function flag=l i n e _ (N1, N2)
	if N1 ( 1 )==0
		k1 =0;
	else
		k1=N2 ( 1 ) /N1 ( 1 );
	end;
	if N1 ( 2 )==0
		k2 =0;
	else
		k2=N2 ( 2 ) /N1 ( 2 );
	end;
	if N1 ( 3 )==0
		k3 =0;
	else
		k3=N2 ( 3 ) /N1 ( 3 );
	end;
	if N1 ( 4 )==0
		k4 =0;
	else
		k4=N2 ( 4 ) /N1 ( 4 );
	end;
	if ( k1 ! = k2 ) | ( k2 != k3 )
		flag =0
		clf; cla;
		plos1 (N1 ( 1 ),N1 ( 2 ),N1 ( 3 ),N1 ( 4 ) );
		hold on
		plos1 (N2 ( 1 ),N2 ( 2 ),N2 ( 3 ),N2 ( 4 ) );
	elseif ( k1 == k2 ) & ( k2 == k3 ) & ( k3 == k4 )
		flag =1;
		clf; cla;
		plos1 (N1 ( 1 ),N1 ( 2 ),N1 ( 3 ),N1 ( 4 ) );
	elseif ( k1 == k2 ) & ( k2 == k3 ) & ( k3!= k4 )
		flag =2;
		disp ( ’Геометрическая фигура не определена!’ )
	end;
end;
% Случай a)
A1=2;B1=-1;C1=0;D1=0;A2=1;B2=1;C2=0;D2=-1;
n1=[A1, B1, C1, D1 ]; n2=[A2, B2, C2, D2 ]; line _ ( n1, n2 )
title ( ’2x-y=0, x+y-1=0’ );
set ( gca, ’View’, [ 110 30 ] );
% Случай b)
A1=1;B1=_1;C1=1;D1=_1;A2=2;B2=_2;C2=2;D2=_2;
n1=[A1, B1, C1, D1 ]; n2=[A2, B2, C2, D2 ]; line _ ( n1, n2 )
title ( ’x-y+z-1=0, 2x-2y+2z-2=0’ );
set ( gca, ’View’, [ 60 30 ] );
% Случай c)
A1=2;B1=-7;C1=12;D1=-4;A2=4;B2=-14;C2=24;D2=-12;
n1=[A1, B1, C1, D1 ]; n2=[A2, B2, C2, D2 ]; line _ ( n1, n2 )
% Результат работы в случае с)
Геометрическая фигура не определена!

Листинг 6.21. Построение прямых, заданных уравнениями плоскостей (пример 6.20).

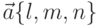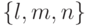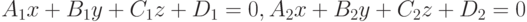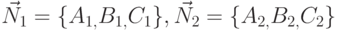Всякий вектор $\vec{a}\{l,m,n\}$ , лежащий на прямой (или параллельный ей), называется направляющим вектором этой прямой. Координаты $\{l, m, n\}$ называются направляющими коэффициентами прямой. За направляющий вектор прямой $A_{1}x+B_{1}y+C_{1}z+D_{1}=0, A_{2}x+B_{2}y+C_{2}z+D_{2}=0$ можно принять векторное произведение $\vec{N}_{1}\times \vec{N}_{2}$ , где $\vec{N}_{1}=\{A_{1,}B_{1,}C_{1}\},\vec{N}_{2}=\{A_{2,}B_{2,}C_{2}\}$ — нормальные векторы плоскостей, образующих прямую.

Дальше >>

Авторизоваться

Введение в Octave

Векторная алгебра и аналитическая геометрия

Вопросы и ответы