|
Возможна ли разработка приложения на Octave с GUI? |
Компания ALT Linux
Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 588 / 66 | Длительность: 20:55:00
Темы: Математика, Программное обеспечение, Физика
Специальности: Математик, Преподаватель, Физик
Лекция 6:
Векторная алгебра и аналитическая геометрия
Пример 6.23. Найти угол между прямыми 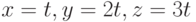 и
и  (истинг 6.24л, рис. 6.20).
(истинг 6.24л, рис. 6.20).
a = [ 1, 2, 3 ]; b = [ 2, 1, 4 ]; % Исходные данные fi =acos ( dot ( a, b ) /norm( a ) /norm( b ) ); fi_1= round ( f i _ 180/ pi ) clf; cla; set( gcf, ’Position’, [ 20, 20, 400, 400 ] ); set( gca, ’Position’, [ .1, .1, .8, .8 ] ); set( gca, ’box’, ’off’ ); xlabel( ’x’ ); ylabel ( ’y’ ); zlabel ( ’z’ ); axis( [ -1, 1, 0, 2, -1, 4 ] ); grid on; t = 0 : 0.1 : 1; x=-1+2* t; y=1+t; z= -1+4* t; % Изображение прямой line ( x, y, z, ’LineWidth’, 5, ’Color’, ’k’ ); % Подписи text( -0.8,1, -1, ’b’, ’FontSize’, 20 ); x=t; y=2* t; z=3* t; % Изображение прямой line( x, y, z, ’LineWidth’, 5, ’Color’, ’k’ ); % Подписи text( 0.2, 0, 0, ’a’, ’FontSize’, 20 ); set( gca, ’View’, [ 30 30 ] ) % Результат fi_1 = 21Листинг 6.24. Нахождение и построение угла между прямыми (пример 6.23).
Прямая 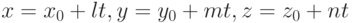 и плоскость
и плоскость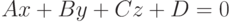 могут иметь одну общую точку, могут не иметь общих точек (прямая параллельна плоскости) и иметь бесконечное множество общих точек (прямая лежит на плоскости).
могут иметь одну общую точку, могут не иметь общих точек (прямая параллельна плоскости) и иметь бесконечное множество общих точек (прямая лежит на плоскости).
Общую точку (если такая существует) плоскости и прямой можно вычислить, если подставить уравнение прямой в уравнение плоскости и найти значение параметра  .
.
Пример 6.24. Найти точку пересечения прямой 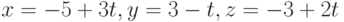 с плоскостью
с плоскостью 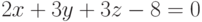 .
.
Выполним расчёты в технике символьных вычислений (листинг 6.25).
symbols % Определение символьных переменных x = sym( "x" ); y = sym( "y" ); z = sym( "z" ); t = sym( "t" ); % Параметрическое уравнение прямой x = -5+3*t; y = 3-t; z = -3+2*t; % Уравнение плоскости f = 2 * x+3*y+3*z -8 % Вычисление значения параметра t t = symfsolve( f, 0 ) % Определение точки пересечения прямой и плоскости x = -5+3*t y = 3-t z = -3+2*t % Результаты вычислений % Уравнение плоскости, выраженное через параметр t f = -18.0+(9.0) * t % Значение параметра t t = 2.0000 % Точка пересечения прямой и плоскости x = 1.00000 y = 1.00000 z = 1.00000Листинг 6.25.