|
Возможна ли разработка приложения на Octave с GUI? |
Векторная алгебра и аналитическая геометрия
Пример 6.6. Найти сумму векторов  и
и  .
.
Если векторы 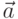 и
и 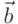 не коллинеарны, то геометрически вектор
не коллинеарны, то геометрически вектор  является диагональю параллелограмма построенного на векторах
является диагональю параллелограмма построенного на векторах 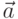 и
и 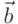 (правило параллелограмма).
(правило параллелограмма).
Листинг 6.7 содержит команды Octave, с помощью которых был решён пример и результаты их работы. Функция 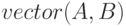 , описана в примере 6.2. Геометрическое решение примера показано на рис. 6.6.
, описана в примере 6.2. Геометрическое решение примера показано на рис. 6.6.
clf; cla; set(gcf, ’Position’, [20, 20, 400, 400]); set(gcf, ’numbertitle’, ’off’) set(gcf, ’name’, ’Vector c=a+b’) set(gca, ’Position’, [.1, .1, .8, .8]); set(gca, ’xlim’, [0, 10]); set(gca, ’ylim’, [0, 10]); set(gca, ’xtick’, [0 : 10]); set(gca, ’ytick’, [0 : 10]); grid on; xlabel(’x’); ylabel(’y’); a = [1, 4]; b = [5, 3]; c =[a(1)+b(1), a(2)+b(2)]% Сумма векторов ma=vector([0, 0], a); % Построение вектора a text (ma(1)+0.3,ma(2)-0.3, ’a’, ’FontSize’, 20); mb=vector([0, 0], b); % Построение вектора b text (mb(1)+0.3,mb(2)-0.3, ’b’, ’FontSize’, 20); mc=vector([0, 0], c); % Построение вектора c=a+b text (mc(1)+0.3,mc(2)-0.3, ’c’, ’FontSize’, 20); line([a(1), c(1)], [a(2), c(2)], ’LineWidth’, 1, ’Color’, ’k’); line([b(1), c(1)], [b(2), c(2)], ’LineWidth’, 1, ’Color’, ’k’); % Результаты работы программы. Координаты вектора c=a+b: c = 67Листинг 6.6. Нахождение суммы векторов (пример 6.6).
Пример 6.7. Выполнить действия над векторами  , где
, где  и
и  .
.
Геометрически вычесть из вектора 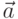 вектор
вектор 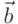 , значит найти такой вектор
, значит найти такой вектор  для которого
для которого  . Иначе говоря, если на векторах
. Иначе говоря, если на векторах  и
и 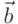 построить треугольник, то
построить треугольник, то  — его третья сторона (правило треугольника).
— его третья сторона (правило треугольника).
Листинг 6.7 содержит команды Octave и результаты работы файла-сценария. Функция 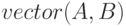 , описана в задаче 6.2. Решение примера показано на рис. 6.7.
, описана в задаче 6.2. Решение примера показано на рис. 6.7.
clf; cla; set(gcf, ’Position’, [20, 20, 400, 400]); set(gcf, ’numbertitle’, ’off’) set(gcf, ’name’, ’Vector c=4a-3b’) set(gca, ’Position’, [.1, .1, .8, .8]); set(gca, ’xlim’, [0, 10]); set(gca, ’ylim’, [0, 10]); set(gca, ’xtick’, [0 : 10]); set(gca, ’ytick’, [0 : 10]); grid on; xlabel(’x’); ylabel(’y’); a = [1, 2]; b = [3, 1]; c =[4*a(1)-3*b(1),4*a(2)-3*b(2)] % Действия над векторами for i =1:4 % Построение вектора 4a ma=vector([0, 0], i*a); end; text(ma(1)+0.3,ma(2)-0.3, ’4a’, ’FontSize’, 20); for i =1:3 % Построение вектора 3b mb=vector([0, 0], i*b); end; text(mb(1)+0.3,mb(2)-0.3, ’3b’, ’FontSize’, 20); % Построение вектора c=4a-3b mc=vector([3*b(1),3*b(2)], [4*a(1),4*a(2)]); text(mc(1)+0.3,mc(2)+0.3, ’c=4a-3b’, ’FontSize’, 20); % Результаты работы программы — координаты отрезка c=4a-3b c = -55Листинг 6.7. Действия над векторами (пример 6.7).
Пример 6.8. Найти углы образуемые осями координат с вектором  .
.
Углы, образуемые положительными направлениями осей с вектором ~a можно рассчитать по
формулам1 — проекция вектора на соответствующую ось. (Прим. редактора).
— проекция вектора на соответствующую ось. (Прим. редактора).
 .
.
Листинг 6.8 содержит команды Octave и результаты работы файла-сценария.
function[U]= ugol(X) % Углы, образуемые осями координат с вектором Х m=sqrt(X(1)^2+X(2)^2+X(3)^2); U=acos(X/m); end; function gr=rad_gr(rad) % Перевод радиан в градусы и минуты gr(1)= round(rad*180/pi); % Градусы gr(2)= round((rad*180/pi-gr(1))*60); % Минуты end; u=ugol([2, -2, -1]) % Вычисление углов в радианах % Углы в градусах и минутах alf=rad_gr(u(1)) bet=rad_gr(u(2)) gam=rad_gr(u(3)) % Результаты работы — углы в радианах u = 0.84107 2.30052 1.91063 % Углы в градусах и минутах alf = 48 11 bet = 132 -11 gam = 109 28Листинг 6.8. Нахождение угла между вектором и осями (пример 6.8).
Скалярным произведением вектора 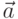 на вектор
на вектор 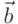 называется произведение их модулей и косинуса угла между ними:
называется произведение их модулей и косинуса угла между ними: 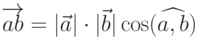 . Если
. Если  и
и  , то
, то  .
.
Пример 6.9. Найти угол между векторами  и
и 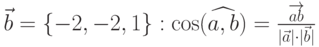 .
.
Текст файла-сценария и результат его работы представлены в листинге 6.9
function gr=rad_gr(rad) % Перевод радиан в градусы и минуты gr(1)= round(rad*180/pi); % Градусы gr(2)= round((rad*180/pi_gr(1))*60); % Минуты end; a = [-2, 1, 2]; b=[-2, -2, 1]; da=sqrt(a(1)^2+a(2)^2+a(3)^2); db=sqrt(b(1)^2+b(2)^2+b(3)^2); ab=sum(a. *b); alf=acos(ab/(da*db)) rad_gr(alf) % Результат — угол в радианах alf = 1.1102 % Угол в градусах ans = 64 -23Листинг 6.9. Нахождение угла между векторами (пример 6.9).

