Внешний поиск

Расширяемое хеширование

Альтернатива B-деревьям, распространяющая применение алгоритмов поразрядного поиска на внешний поиск, была разработана в 1978 г. Фагином (Fagin), Нивергельтом (Nievergelt), Пиппенгером (Pippenger) и Стронгом (Strong). Их метод, названный расширяемым хешированием (extendible hashing), приводит к реализации операции найти, требующей в типичных приложениях всего одной-двух проб. Для соответствующей реализации операции вставить также (почти всегда) нужны лишь одна-две пробы.

Расширяемое хеширование сочетает свойства методов хеширования, алгоритмов на основе многопутевых trie-деревьев и методов последовательного доступа. Подобно методам хеширования, описанным в "Хеширование" , расширяемое хеширование представляет собой рандомизированный алгоритм — поэтому сначала необходимо определить хеш-функцию, которая преобразует ключи в целые числа (см. раздел 14.1 "Хеширование" ). Для простоты в этом разделе мы будем просто считать, что ключи являются случайными битовыми строками фиксированной длины. Подобно алгоритмам с использованием многопутевых trie-деревьев из "Поразрядный поиск" , расширяемое хеширование начинает поиск, используя ведущие разряды ключей в качестве индексных указателей в таблице, размер которой равен степени 2. Подобно алгоритмам на основе B-деревьев, при использовании расширяемого хеширования элементы хранятся в страницах, которые при заполнении разбиваются на две части. Подобно методам индексно-последовательного доступа, расширяемое хеширование поддерживает каталог, указывающий, где можно найти страницу, в которой находятся соответствующие искомому ключу элементы. Сочетая эти знакомые свойства в одном алгоритме, расширяемое хеширование как нельзя более подходит для завершения знакомства с алгоритмами поиска.

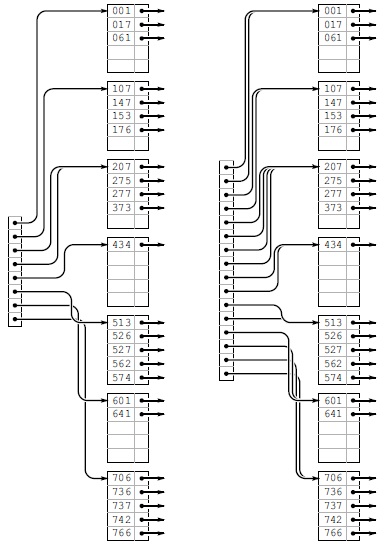
Предположим, что количество доступных страниц диска является степенью 2 — скажем, 2^d. Тогда можно поддерживать каталог 2^d различных ссылок на страницы, использовать d разрядов ключей для индексного доступа к этому каталогу и хранить в одной и той же странице все ключи, первые к разрядов которых совпадают (см. рис. 16.10). Как и в случае B-деревьев, элементы на страницах хранятся упорядоченными, и, найдя страницу, которая соответствует элементу с заданным искомым ключом, мы выполняем в ней последовательный поиск.

На рис. 16.10 приведены две базовых концепции, лежащие в основе расширяемого хеширования. Во-первых, совсем не обязательно поддерживать 2^d страниц. То есть можно иметь несколько записей каталога со ссылками на одну и ту же страницу, объединив на одной странице ключи с различными значениями, первые d разрядов которых совпадают.

Рис. 16.10. Индексы страниц каталога

Каталог, состоящий из восьми записей, позволяет содержать до 40 ключей, храня все записи с первыми 3 совпадающими разрядами на одной странице, обратиться к которой можно через ссылку, хранящуюся в каталоге (слева). Запись 0 каталога содержит ссылку на страницу, которая содержит все ключи, начинающиеся с 000; запись 1 таблицы содержит ссылку на страницу, которая содержит все ключи, начинающиеся с 001; запись 2 таблицы содержит ссылку на страницу, которая содержит все ключи, начинающиеся с 010, и т.д. Если некоторые страницы заполнены не полностью, количество требуемых страниц можно уменьшить, используя несколько ссылок на одну и ту же страницу. В данном примере (слева) ключ 3 73 находится на той же странице, что и ключи, начинающиеся с 2; эта страница определена как содержащая элементы с ключами, первые два разряда которых равны 01.

Если удвоить размер каталога и скопировать каждую ссылку, то получим структуру, которую можно индексировать первыми 4 разрядами искомого ключа (справа). Например, последняя страница по-прежнему определяется как содержащая элементы с ключами, первые три разряда которых равны 111, и она будет доступна через каталог для искомых ключей с первыми 4 разрядами 1110 или 1111. Этот больший каталог допускает увеличение таблицы.

Это не помешает быстро выполнять поиск в структуре и в то же время позволяет находить страницу с искомым ключом, используя ведущие разряды ключа для индексного доступа к каталогу. Во-вторых, для увеличения емкости таблицы можно удваивать размер каталога.

В частности, структура данных, которая применяется для расширяемого хеширования, значительно проще используемой в B-деревьях. Она состоит из страниц, содержащих до M элементов, и каталога с 2^d ссылками на страницы (см. программу 16.5). Ссылка в ячейке каталога x указывает на страницу, содержащую все элементы с ведущими d разрядами, равными х. Значение d выбирается достаточно большим, чтобы в каждой странице гарантированно хранилось менее M элементов. Реализация операции найти проста: мы используем ведущие d разрядов ключа для индексного доступа к каталогу, что обеспечивает доступ к странице, которая содержит все элементы с соответствующими ключами, а затем выполняем последовательный поиск такого элемента на данной странице (см. программу 16.6).

Для поддержки операции вставить структура данных должна быть несколько более сложной, однако одно из ее свойств заключается в том, что этот алгоритм поиска успешно работает без каких-либо модификаций. Но сначала необходимо ответить на следующие вопросы:

• Что делать, когда количество элементов на странице превысит ее емкость?
• Какой размер каталога следует использовать?

Программа 16.5. Структуры данных для расширяемого хеширования

Расширяемая хеш-таблица — это каталог ссылок на страницы (подобно внешним узлам в B-деревьях), которые содержат до 2M элементов. Каждая страница содержит также счетчик (m) количества элементов в странице и целое число (k), задающее количество ведущих разрядов, которые должны совпадать в ключах элементов. Как обычно, N — количество элементов в таблице. Переменная d задает количество разрядов, которые используются для индексации в каталоге, а D — количество записей в каталоге; таким образом, D = 2^d . Вначале таблица создается соответствующей каталогу размером 1, со ссылкой на пустую страницу.

template <class Item, class Key>
class ST
  { private:
      struct node
        { int m; Item b[M]; int k;
          node() { m = 0; k = 0; }
        } ;
      typedef node *link;
      link* dir;
      Item nullItem;
      int N, d, D;
     public:
       ST(int maxN)
         { N = 0; d = 0; D = 1;
           dir = new link[D];
           dir[0] = new node;
         }
  } ;
      

Программа 16.6. Поиск в таблице расширяемого хеширования

Поиск в таблице расширяемого хеширования сводится лишь к использованию ведущих разрядов ключа для индексного доступа к каталогу и выполнению на указанной странице последовательного поиска элемента, ключ которого равен искомому. Единственное выдвигаемое при этом требование — каждая запись каталога должна указывать на страницу, которая гарантированно содержит все элементы таблицы символов, начинающиеся с указанных разрядов.

  private:
    Item search(link h, Key v)
    { for (int j = 0; j < h->m; j++)
      if (v == h->b[j].key()) return h->b[j];
      return nullItem;
    }
  public:
    Item search(Key v)
      { return search(dir[bits(v, 0, d)], v); }
      

Например, в примере, приведенном на рис. 16.10, нельзя использовать d = 2, поскольку некоторые страницы окажутся переполненными, и нельзя использовать d = 5, поскольку слишком много страниц будут пустыми. Как обычно, наибольший интерес вызывает поддержка операции вставить для АТД таблицы символов, чтобы, например, структура могла постепенно разрастаться по мере выполнения ряда чередующихся операций найти и вставить. Принятие такой точки зрения соответствует уточнению первого вопроса:

• Что делать, если нужно вставить элемент в заполненную страницу?

Например, в примере на рис. 16.10 нельзя вставить элемент, ключ которого начинается с 5 или 7, поскольку соответствующие страницы заполнены.

Некоторые d-разрядные последовательности могут не появляться ни в одном из ключей. В определении 16.3 никак не упомянуты соответствующие записи каталога, хотя существует естественный способ организации ссылок на пустые страницы, который будет рассмотрен чуть ниже.

Для поддержания этих характеристик при разрастании таблицы мы используем две базовые операции: разбиение страницы, при котором некоторые ключи с полной страницы переносятся на другую страницу, и разбиение каталога, при котором размер каталога удваивается, а значение d увеличивается на 1. А именно, при заполнении страницы мы разбиваем ее на две, используя для определения элементов, которые должны быть перемещены на новую страницу, самый левый разряд, которым различаются ключи,. При разбиении страницы соответствующим образом корректируются записи каталога, а при необходимости его размер удваивается.

Как обычно, лучший способ понять алгоритм — это проследить его работу при вставке набора ключей в первоначально пустую таблицу. Каждая из ситуаций, которые должен обрабатывать алгоритм, проявляется в начале процесса в простейшей форме, и принципы, лежащие в основе алгоритма, вскоре становятся понятными.

На рис. 16.13—16.13 показано построение расширяемой хеш-таблицы для набора 25 восьмеричных ключей, рассматриваемого в этой главе. Как и в B-деревьях, большинство вставок не приводят к переполнению: они просто добавляют ключ в страницу. Поскольку процесс начинается с одной страницы, а завершается восемью, можно сделать вывод, что семь вставок вызвали разбиение страниц. Поскольку в начале размер каталога равен 1, а в конце — 16, можно сделать вывод, что четыре вставки привели к разбиению каталога.

Рис. 16.11. Построение расширяемой хеш-таблицы, часть 1

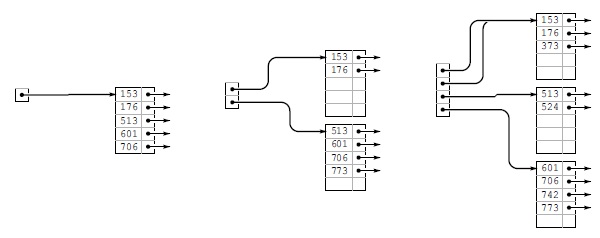
Как и в B-деревьях, первые пять вставок в расширяемую хеш-таблицу приходятся на одну страницу (слева). Затем, при вставке ключа 773, выполняется разбиение на две страницы (одна содержит все ключи, начинающиеся с бита 0, другая — все ключи, начинающиеся с бита 1), а размер каталога удваивается, чтобы он содержал по одному указателю на каждую из страниц (в центре). Ключ 742 вставляется в нижнюю страницу (т.к. он начинается с бита 1), а ключ 373 — в верхнюю страницу (т.к. он начинается с бита 0), но затем нижнюю страницу приходится разбить, чтобы было куда поместить ключ 52 4. Для выполнения этого разбиения все элементы, ключи которых начинаются с битов 10, помещаются на одну страницу, а все элементы, ключи которых начинаются с битов 11 — на другую, и размер каталога снова удваивается, чтобы в нем могли поместиться указатели на обе эти страницы (справа). Каталог содержит две ссылки на страницу, содержащую элементы с ключами, которые начинаются с бита 0: одна для ключей, которые начинаются с битов 00, и другая для ключей, которые начинаются с битов 01.

Программа 16.7 является реализацией операции вставить для расширяемой хеш-таблицы. Сначала, как и при поиске, с помощью единственного обращения к каталогу мы находим страницу, которая может содержать искомый ключ. Затем мы вставляем в нее новый элемент, как это делалось для внешних узлов в B-деревьях (см. программу 16.2). Если в результате этой вставки в узле оказывается M элементов, вызывается функция разбиения — опять же, как и для B-деревьев, правда, на этот раз она сложнее. Каждая страница содержит число к ведущих разрядов, которые совпадают в ключах всех элементов на этой странице, и, поскольку разряды нумеруются слева направо, начиная с 0, к задает также индекс разряда, который необходимо проверить для определения способа разбиения элементов.

Рис. 16.12. Построение расширяемой хеш-таблицы, часть 2

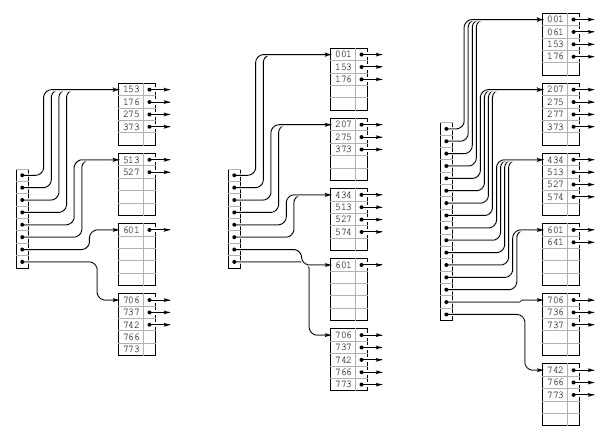
Ключи 766 и 275 вставляются в крайнее правое B-дерево, показанное на рис. 16.11, без разбиения узлов (слева). Затем, при вставке ключа 737, нижняя страницаразбивается, и, поскольку существует только одна ссылка на нижнюю страницу, это приводит кразбиению каталога (в центре). Затем выполняется вставка ключей 574, 434, 641 и 207, после чего необходимо разбиение верхней страницы (справа).

Рис. 16.13. Построение расширяемой хеш-таблицы, часть 3

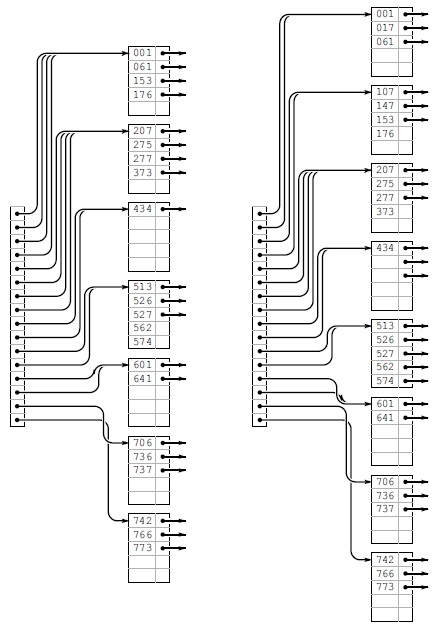
Продолжая пример, приведенный на рис. 16.11 и 16.12, мы вставляем 5 ключей 526, 562, 017, 107 и 147 в крайнее правое B-дерево, показанное на рис. 16.6. Разбиение узлов происходит при вставке ключей 526 (слева) и 107 (справа).