Внешний поиск

B-деревья

Для построения структур поиска, которые могут быть эффективны в динамических ситуациях, мы будем строить многопутевые деревья, но при этом откажемся от ограничения, что каждый узел должен содержать точно M записей. Вместо этого выдвинем условие, что каждый узел должен иметь не более M записей, чтобы они помещались на странице, но узлы могут иметь и меньше записей. Чтобы гарантировать, что узлы имеют достаточное количество записей для обеспечения ветвления, необходимого для предотвращения увеличения длины путей, мы также потребуем, чтобы все узлы имели не менее (допустим) M/2 записей — за исключением, быть может, корня, который должен иметь не менее одной записи (двух ссылок). Причина этого исключения для корня станет понятна при подробном рассмотрении алгоритма построения. Байер (Bayer) и МакКрейт (McCreight) первыми (в 1970 г.) исследовали возможность использования многопутевых сбалансированных деревьев для внешнего поиска и назвали такие деревья B-деревьями. Термин B-дерево часто используется для описания именно той структуры данных, которая строится алгоритмом, предложенным Байером и МакКрейтом; мы же будем использовать его в качестве общего термина для обозначения семейства похожих алгоритмов.

Мы уже встречались с реализацией B-дерева: из определений 13.1 и 13.2 видно, что B-деревья четвертого порядка, в которых каждый узел содержит не более 4 и не менее 2 ссылок, являются ни чем иным, как сбалансированными 2-3-4-деревьями, описанными в "Сбалансированные деревья" . Лежащая в их основе абстракция допускает непосредственное обобщение, так что B-деревья можно реализовать, обобщив реализации нисходящего 2-3-4-дерева, описанные в "Сбалансированные деревья" . Однако различия между внешним и внутренним поиском, упомянутые в разделе 16.1, приводят к ряду различий в реализациях.

• обобщает 2-3-4-деревья до деревьев, имеющих от M/2 до M узлов
• представляет многопутевые узлы в виде массива элементов и ссылок
• реализует индекс, а не структуру поиска, содержащую элементы
• выполняет восходящее разбиение
• отделяет индексы от элементов

Два последних свойства в этом перечне несущественны, однако во многих ситуациях удобны и часто применяются в реализациях B-деревьев.

На рис. 16.4 показано абстрактное 4-5-6-7-8-дерево, являющееся обобщением 2-3-4-дерева из "Сбалансированные деревья" . Обобщение очевидно: 4-узлы имеют три ключа и четыре ссылки, 5-узлы — четыре ключа и пять ссылок и т.д.: по одной ссылке для каждого возможного интервала ключей. Поиск начинается с корня и проходит от одного узла к другому, определяя в текущем узле интервал, который соответствуюет искомому ключу, и переходя к следующему узлу по соответствующей ссылке. Поиск завершается успешно, если ключ поиска находится в любом из рассмотренных узлов, и неудачно, если он дошел до низа дерева, не обнаружив искомый ключ. Как и в случае 2-3-4-деревьев, новый ключ можно вставить после выполнения поиска в нижнюю часть дерева, если при спуске вниз по дереву выполняется разбиение заполненных узлов: если корень является 8-узлом, он заменяется 2-узлом, связанным с двумя 4-узлами. Затем, каждый раз, когда встречается k-узел с присоединенным 8-узлом, он заменяется (к+1)-узлом с двумя присоединенными 4-узлами. Это правило гарантирует наличие места для вставки нового узла по достижении нижней части дерева.

Или же, как и в "Сбалансированные деревья" применительно к 2-3-4-деревьям, разбиение можно выполнять снизу вверх: после выполнения поиска новый ключ вставляется в нижний узел, если только тот не является 8-узлом — в этом случае он разбивается на два 4-узла со вставкой среднего ключа и двух ссылок в его родительский узел. Восходящее разбиение выполняется до тех пор, пока не встретится узел-предок, отличный от 8-узла.

Замена в предыдущих двух абзацах 4 на M/2, а 8 — на M позволяет преобразовать приведенные описания в описания поиска и вставки в М/2-...-М-деревьях для любого положительного четного M (см. упражнение 16.9).

Рис. 16.4. 4-5-6-7-8-дерево

На рисунке показано обобщение 2-3-4-деревьев, которое построено из узлов, содержащих от 4 до 8ссылок (и соответственно от 3 до 7ключей). Как и в случае 2-3-4-деревьев, мы поддерживаем высоту деревьев постоянной, разбивая встречающиеся 8-узлы при работе нисходящего или восходящего алгоритма вставки. Например, для вставки в это дерево еще одного ключа J нужно сначала разбить 8-узел на два 4-узла, а затем вставить ключ M в корень, преобразовав его в 6-узел. При разбиении корня возможно лишь создание нового корня, который будет 2-узлом — поэтому корень не подчиняется общему правилу, согласно которому узлы должны содержать не менее четырех ссылок.

Алгоритмы B-деревьев построены на основе этого базового набора абстракций. Как и в "Сбалансированные деревья" , существует значительная свобода в выборе конкретных представлений таких деревьев. Например, можно использовать расширенное RB-представление (см. упражнение 13.69). Для внешнего поиска мы используем еще более простое представление в виде упорядоченного массива, выбирая достаточно большое значение M, чтобы M-узлы заполняли всю страницу. Коэффициент ветвления равен по меньшей мере M/2, поэтому, как следует из текста после леммы 16.1, количество проб, необходимое для выполнения любого поиска или вставки, практически постоянно.

Вместо реализации только что описанного метода рассмотрим вариант, обобщающий стандартный индексный указатель, рассмотренный в разделе 16.1. Будем хранить ключи со ссылками на элементы во внешних страницах в нижней части дерева, а копии ключей со ссылками на страницы — во внутренних страницах. Мы вставляем новые элементы в нижнюю часть, а затем используем базовую абстракцию M/2-...-M дерева. Если страница содержит M записей, мы разбиваем ее на две страницы с M/2 записями в каждой и вставляем в родительскую страницу ссылку на новую страницу. При разбиении корня мы создаем новый корень с двумя дочерними узлами, тем самым увеличивая высоту дерева на 1.

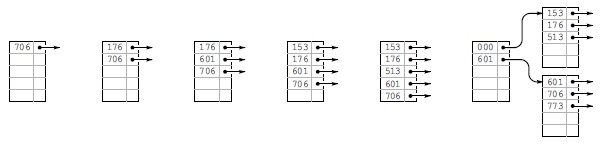
На рис. 16.5 рис. 16.7—16.7 показан процесс построения B-дерева вставками ключей, показанных на рис. 16.1 (в приведенном порядке) в первоначально пустое дерево при M= 5.

Рис. 16.5. Построение B-дерева, часть 1

Здесь показаны шесть вставок в первоначально пустое B-дерево, построенное из страниц, которые могут содержать пять ключей и ссылок, при использовании 3-значных восьмеричных ключей (9-разрядных двоичных чисел). Ключи в страницах хранятся по порядку. Шестая вставка приводит к разбиению на два внешних узла с тремя ключами в каждом и внутренний узел, служащий в качестве индекса: его первая запись указывает на страницу, содержащую все ключи, которые больше или равны 000, но меньше 601, а вторая запись — на страницу, содержащую все ключи, которые больше или равны 601.

Рис. 16.6. Построение B-дерева, часть 2

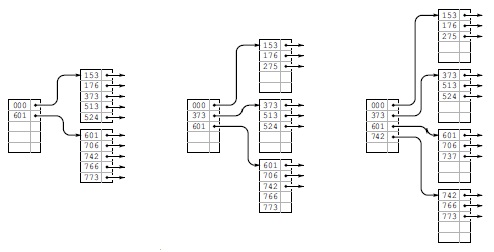
После вставки четырех ключей 742, 373, 524 и 766 в самое правое B-дерево на рис. 16.5 обе внешние страницы оказываются заполненными (слева). Затем, при вставке ключа 2 7 5, первая страница разбивается с передачей ссылки на новую страницу (вместе с ее наименьшим ключом 37 3) вверх по индексу (в центре). Далее, при вставке ключа 7 37 разбивается нижняя страница, также с передачей ссылки на новую страницу вверх по индексу (справа).

Рис. 16.7. Построение B-дерева, часть 3

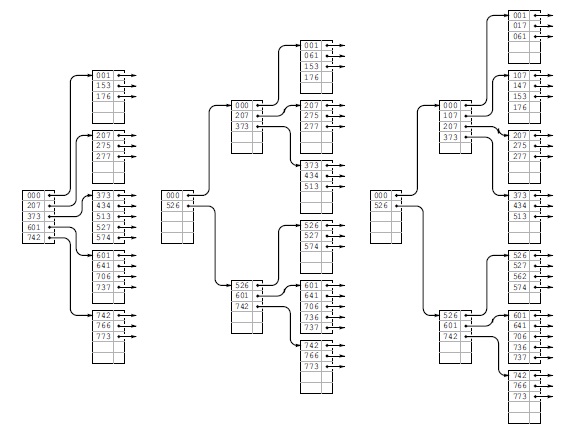
Продолжая наш пример, мы вставляем 13 ключей 574, 434, 641, 207, 001, 277, 061, 736, 526, 562, 017, 107 и 147 в самое правое B-дерево на рис. 16.6. Разбиения узлов выполняются при вставке ключей 277 (слева), 526 (в центре) и 107 (справа). Разбиение узла, вызванное вставкой ключа 52 6, приводит также к разбиению индексной страницы и увеличению высоты дерева на единицу.

Выполнение вставок сводится лишь к добавлению элемента в страницу, но на основании структуры результирующего дерева можно определить важные события, происшедшие во время его построения. Дерево содержит семь внешних страниц, поэтому должно было быть выполнено шесть разбиений внешних узлов, и поскольку его высота равна 3, корень дерева должен был разбиваться дважды. Эти события описаны в подписях к рисункам.

В программе 16.1 приведены определения типов для узлов нашей реализации B-дерева. Мы не указываем подробно структуру узлов, как в рабочей реализации, т.к. для этого потребовались бы ссылки на конкретные страницы диска. Для простоты мы используем один тип узлов, каждый узел состоит из массива записей, а каждая запись содержит элемент, ключ и ссылку. Каждый узел содержит также счетчик активных записей. Мы не обращаемся к элементам во внутренних узлах, не обращаемся к ссылкам во внешних узлах, и не обращаемся к ключам в элементах дерева. При использовании конкретной структуры данных в реальном приложении можно сэкономить память с помощью конструкций наподобие union или производных классов. Можно было бы также сэкономить память ценой увеличения времени выполнения, используя везде в дереве вместо ключей ссылки на элементы. Такие конструктивные решения достигаются очевидными изменениями кода и зависят от конкретного характера ключей, элементов и ссылок в приложении.

С помощью этих определений и рассмотренных примеров деревьев, код выполнения операции найти, приведенный в программе 16.2, реализуется элементарно. Для внешних узлов мы просматриваем массив узлов, чтобы найти ключ, соответствующий искомому ключу, и возвращаем связанный с ним элемент, если поиск успешен, и пустой элемент, если неудачен. Для внутренних узлов мы просматриваем массив узлов, чтобы найти ссылку на уникальное поддерево, которое может содержать искомый ключ.

Программа 16.3 является реализацией операции вставить для B-деревьев; в ней также применяется рекурсивный подход, используемый во многих других реализациях деревьев поиска из глав 13 и 15. Эта реализация является восходящей, т.к. проверка, нужно ли разбивать узел, выполняется после рекурсивного вызова — поэтому первым разбивается внешний узел. Разбиение требует передачи новой ссылки наверх к родительскому узлу разбиваемого узла, который, в свою очередь, может нуждаться в разбиении и передаче ссылки его родительскому узлу и т.д. — возможно, вплоть до корня дерева (при разбиении корня создается новый корень с двумя дочерними поддеревьями).

В противоположность этому в реализации 2-3-4-дерева в программе 13.6 проверка, нужно ли разбивать узел, выполняется перед рекурсивным вызовом, и поэтому разбиение выполняется при спуске вниз по дереву. Для B-деревьев можно воспользоваться и нисходящим подходом (см. упражнение 16.10). Во многих приложениях, использующих B-деревья, это различие между нисходящим и восходящим подходами несущественно, поскольку такие деревья являются очень плоскими.

Код разбиения узла приведен в программе 16.4. В нем переменная M должна иметь четное значение, и каждый узел дерева может содержать только M — 1 элемент. Этот подход позволяет вставлять M-й элемент в узел перед разбиением этого узла и значительно упрощает код, не оказывая особого влияния на затраты (см. упражнения 16.20 и 16.21). Для простоты аналитических выкладок, приведенных далее в этом разделе, мы вводим ограничение, что количество элементов каждого узла должно быть не больше M; реальные различия несущественны. В нисходящей реализации эта технология не нужна, т.к. в ней наличие свободного места в каждом узле для вставки нового ключа обеспечивается автоматически.

Программа 16.1. Определения типов узлов B-дерева

Каждый узел в B-дереве содержит массив и счетчик количества активных записей в этом массиве. Каждая запись массива представляет собой ключ, элемент и ссылку на узел. Во внутренних узлах используются только ключи и ссылки; во внешних узлах используются только ключи и элементы. Новые узлы создаются пустыми, для чего обнуляется поле счетчика.

  template <class Item, class Key>
  struct entry
    { Key key; Item item; struct node *next; };
  struct node
    { int m; entry<Item, Key> b[M];
      node() { m = 0; }
    };
  typedef node *link;