|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Внешний поиск
Программа 16.7. Вставка в расширяемую хеш-таблицу
Чтобы вставить элемент в расширяемую хеш-таблицу, мы выполняем его поиск, а затем вставляем элемент в найденную страницу (и разбиваем ее, если вставка вызывает переполнение). Общая схема не отличается от используемой для B-деревьев, но алгоритмы поиска и разбиения иные. Функция разбиения создает новый узел, затем проверяет к-й бит (считая слева) ключа каждого элемента: если этот бит равен 0, элемент остается в старом узле; если 1 — перемещается в новый. В поле " количество одинаковых ведущих разрядов " обоих узлов после разбиения заносится значение к + 1. Если этот процесс не приводит к наличию по меньшей мере одного ключа в каждом узле, разбиение выполняется снова, пока элементы не станут разделены. И, наконец, мы вставляем ссылку на новый узел в каталог.
private:
void split(link h)
{ link t = new node;
while (h->m == 0 || h->m == M)
{ h->m = t->m = 0;
for (int j = 0; j < M; j++)
if (bits(h->b[j].key(), h->k, 1) == 0)
h->b[h->m++] = h->b[j];
else
t->b[t->m++] = h->b[j];
t->k = ++(h->k);
}
insertDIR(t, t->k);
}
void insert(link h, Item x)
{ int j; Key v = x.key();
for (j = 0; j < h->m; j++)
if (v < h->b[j].key()) break;
for (int i = (h->m)++; i > j; i—-)
h->b[i] = h->b[i-1];
h->b[j] = x;
if (h->m == M) split(h);
}
public:
void insert(Item x)
{ insert(dir[bits(x.key(), 0, d)], x); }
Следовательно, для разбиения страницы мы создаем новую страницу, затем помещаем все элементы, для которых данный разряд равен 0, в старую страницу, а все элементы, для которых он равен 1 — в новую страницу, а затем для обеих страниц устанавливаем значение счетчика разрядов равным к + 1. Вообще-то возможен случай, когда в полном узле все ключи имеют одинаковое значение разряда к. В этом случае нужно просто перейти к следующему разряду и продолжать этот процесс до тех пор, пока каждая страница не будет содержать по меньшей мере один элемент. Однажды этот процесс должен завершиться, если только не имеется M значений одного и того же ключа. Вскоре мы рассмотрим и этот случай.
Как и в случае B-деревьев, на каждой странице резервируется свободное место для одной лишней записи, которая позволяет выполнять разбиение после вставки — это упрощает код. Данный прием почти не влияет на производительность, так что при анализе им можно пренебречь.
При создании новой страницы необходимо вставить в каталог ссылку на нее. Код, выполняющий эту вставку, приведен в программе 16.8. Простейшим является случай, когда перед вставкой каталог содержит ровно две ссылки на страницу, которая будет разбита. В этом случае нужно лишь записать вторую ссылку, указывающую на новую страницу. Если количество разрядов к, которое нужно для различения ключей на новой странице, превышает количество разрядов d для доступа к каталогу, то размер каталога нужно увеличить, чтобы в нем могла поместиться новая запись. И, наконец, выполняется соответствующее изменение ссылок в каталоге.
Если более M элементов имеют одинаковые ключи, таблица переполняется, и программа 16.7 зацикливается, пытаясь различить эти ключи. Есть еще одна похожая проблема: каталог может оказаться неоправданно большим, если ключи имеют очень много совпадающих ведущих разрядов. Эта ситуация похожа на излишнее время, требуемое для выполнения MSD-сортировки файлов с большим количеством одинаковых ключей или длинными последовательностями разрядов, в которых они совпадают. Решение этих проблем зависит от рандомизации, обеспечиваемой хеш-функцией (см. упражнение 16.43). Но даже при использовании хеширования в случае большого количества одинаковых ключей приходится предпринимать специальные действия, поскольку хеш-функции отображают равные ключи в равные хеш-значения. Повторяющиеся ключи могут сделать каталог неестественно большим, а при наличии большего количества равных ключей, чем помещается на одной странице, алгоритм просто перестает работать. Следовательно, при использовании этого кода необходимо добавить проверки, предотвращающие возникновение таких условий (см. упражнение 16.35).
С точки зрения производительности наибольший интерес представляют количество используемых страниц (как и в случае B-деревьев) и размер каталога. Для этого алгоритма рандомизация обеспечивается хеш-функциями, поэтому характеристики производительности для среднего случая верны и для любой последовательности N вставок различных ключей.
Программа 16.8. Вставка в каталог расширяемого хеширования
Этот с виду простой код лежит в основе процесса расширяемого хеширования. Вначале имеется ссылка t на узел, содержащий элементы с совпадающими первыми к разрядами, которую нужно вставить в каталог. В простейшем случае, если d и k равны, достаточно просто записать t в d[x], где x — значение первых d разрядов t->b[0] (и всех остальных элементов на странице). Если k больше d, размер каталога нужно удваивать, пока d и k не станут равны. Если k меньше d, необходимо записать более одной ссылки — в первом цикле for вычисляется количество необходимых ссылок ( 2d-k ), а во втором выполняется собственно установка.
void insertDIR(link t, int k)
{ int i, m, x = bits(t->b[0].key(), 0, k);
while (d < k)
{ link *old = dir;
d += 1; D += D;
dir = new link[D];
for (i = 0; i < D; i++) dir[i] = old[i/2];
if (d < k) dir[bits(x, 0, d)A1] = new node;
}
for (m = 1; k < d; k++) m *= 2;
for (i = 0; i < m; i++) dir[x*m+i] = t;
}
Лемма 16.5. Для реализации расширяемого хеширования в случае файла, содержащего N элементов, и страниц, которые могут содержать M элементов, в среднем требуется около 1,44 N/M страниц. Ожидаемое количество записей в каталоге приблизительно равно 3,92(N1/M/M)(N/M) .
Этот (достаточно глубокий) результат дополняет анализ trie-деревьев, кратко рассмотренный в предыдущей главе (см. раздел ссылок). Точные значения констант для количества страниц и размера каталога соответственно равны lg e = 1/ln 2 и e lg e = e / ln 2, хотя точные значения величин колеблются вокруг указанных средних значений. Это неудивительно, поскольку, например, нужно принимать во внимание, что размер каталога должен являться степенью 2. 
Обратите внимание, что размер каталога возрастает быстрее чем линейно относительно N, особенно при малых M. Однако для значений N и M, встречающихся на практике, значение N1/M достаточно близко к 1, поэтому реально можно ожидать, что каталог будет иметь около 4 N/M записей.
Мы считаем, что каталог — это массив ссылок. Его можно хранить в памяти или, если он слишком велик, в памяти можно хранить корневой узел, указывающий местонахождение страниц каталога, используя такую же схему индексирования. Или же можно добавить еще один уровень, индексируя первый уровень, скажем, по первым 10 разрядам, а второй — по остальным разрядам (см. упражнение 16.36).
Как и в случае B-деревьев, реализация всех остальных операций таблицы символов оставлена в качестве упражнений (см. упражнения 16.38—16.41). И так же, как и в случае B-деревьев, правильная реализация операции удалить представляет собой сложную задачу, но можно разрешить наличие мало заполненных страниц — эта легко реализуемая альтернатива может оказаться эффективной во многих возникающих на практике ситуациях.
Упражнения
16.27. Сколько страниц будут пусыми, если на рис. 16.10 использовать каталог, размер которого равен 32?
16.28. Нарисуйте рисунки наподобие рис. 16.13, иллюстрирующие процесс вставки ключей 562, 221, 240, 771, 274, 233, 401, 273 и 201 в указанном порядке в первоначально пустое дерево, при M= 5.
16.29. Нарисуйте рисунки наподобие рис. 16.13, иллюстрирующие процесс вставки ключей 562, 221, 240, 771, 274, 233, 401, 273 и 201 в указанном порядке в первоначально пустое дерево, при M= 3.
16.30. Допустим, что имеется массив упорядоченных элементов. Опишите, как можно было бы определить размер каталога расширяемой хеш-таблицы, соответствующей этому набору элементов.
16.31. Напишите программу, которая строит расширяемую хеш-таблицу из массива упорядоченных элементов, выполняя два прохода по элементам: один для определения размера каталога (см. упражнение 16.30) и второй — для распределения элементов по страницам и заполнения каталога.
16.32. Приведите набор ключей, для которого соответствующая расширяемая хеш-таблица имеет каталог размером 16, если в одной странице помещается 8 ссылок.
16.33. Создайте рисунок наподобие рис. 16.8 для расширяемого хеширования.
16.34. Напишите программу для вычисления среднего количества внешних страниц и среднего размера каталога для расширяемой хеш-таблицы, построенной N случайными вставками в первоначально пустое дерево, при емкости страницы M. Вычислите процент неиспользуемой памяти при M= 10, 100 и 1000 и N= 103, 104, 105 и 106 .
16.35. Добавьте в программу 16.7 проверки, необходимые для предотвращения неправильной работы при вставке в таблицу слишком большого количества одинаковых ключей или ключей, у которых совпадает слишком много ведущих разрядов.
16.36. Измените реализацию расширяемого хеширования, приведенную в программах 16.5—16.7, так, чтобы в ней использовался двухуровневый каталог, в каждом узле которого содержится не более M указателей. Обратите особое внимание на выбор действий, когда каталог впервые разрастается с одного до двух уровней.
16.37. Измените реализацию расширяемого хеширования, приведенную в программах 16.5—16.7, чтобы в структуре данных в одной странице могло находиться M элементов.
16.38. Реализуйте операцию сортировать для расширяемой хеш-таблицы.
16.39. Реализуйте операцию выбрать для расширяемой хеш-таблицы.
16.40. Реализуйте операцию удалить для расширяемой хеш-таблицы.
16.41. Реализуйте операцию удалить для расширяемой хеш-таблицы, используя метод, описанный в упражнении 16.25.
16.42. Разработайте версию расширяемого хеширования, которая при разбиении каталога разбивает и страницы, чтобы каждая ссылка каталога указывала на уникальную страницу. Экспериментально сравните производительность этой реализации с производительностью стандартной реализации.
16.43. Экспериментально определите количество случайных чисел, которые будут сгенерированы, прежде чем встретятся более M чисел с одинаковыми d начальными разрядами, при M= 10, 100 и 1000 и при 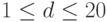 .
.
16.44. Измените алгоритм хеширования с цепочками переполнения (программа 14.3), чтобы в нем использовалась хеш-таблица размером 2M и элементы хранились в страницах размером 2M. Другими словами, когда страница заполняется, к ней привязывается новая пустая страница, чтобы каждая запись хеш-таблицы указывала на связный список страниц. Экспериментально определите среднее количество проб, необходимых для выполнения поиска после построения таблицы из N элементов со случайными ключами, при M= 10, 100 и 1000 и N= 103, 104, 105 и 106 .
16.45. Измените алгоритм двойного хеширования (программа 14.6), чтобы в нем использовались страницы размером 2M, а обращения к полным страницам интерпретировались как " коллизии " . Экспериментально определите среднее количество проб, необходимое для выполнения поиска после построения таблицы из N элементов со случайными ключами, при M= 10, 100 и 1000 и N= 103, 104, 105 и 106 , при начальном размере таблицы равном 3N/2M.
