|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Элементарные методы сортировки
Сортировка связных списков
Как мы знаем из "Элементарные структуры данных" , массивы и связные списки представляют собой два самых основных способа структурирования данных. Кроме того, в качестве примера обработки списков мы уже рассмотрели реализацию сортировки вставками связных списков (см. программу 3.11 в разделе 3.4 "Элементарные структуры данных" ). Во всех реализациях сортировок, рассмотренные к этому моменту, предполагается, что сортируемые данные представлены в виде массива. Эти реализации нельзя использовать непосредственно, если для организации данных используются связные списки. Сами алгоритмы могут оказаться полезными, но только если они выполняют последовательную обработку данных, которую могут эффективно поддерживать связные списки.
Программа 6.15 задает интерфейс типа данных связного списка, похожий на приведенный в программе 6.7. Программа 6.15 позволяет написать драйвер, соответствующий программе 6.6, в одной строке:
main(int argc, char *argv[])
{ showlist(sortlist(scanlist(atoi(argv[1])))); }
Большая часть работы (включая и распределение памяти) ложится на реализации связного списка и функции sort. Как и в случае драйвера для массива, необходимо иметь возможность инициализировать этот список (из стандартного ввода либо случайными значениями), выводить его содержимое и, разумеется, сортировать его. Как обычно, в качестве типа данных сортируемых элементов используется Item — как и в разделе 6.7. Код, реализующий подпрограммы для этого интерфейса, стандартен для связных списков, которые были подробно рассмотрены в "Элементарные структуры данных" , и поэтому оставлен в качестве упражнения.
Программа 6.15. Определение интерфейса для типа связного списка
Данный интерфейс для связных списков похож на интерфейс для массивов, представленный в программе 6.7. Функция randomlist строит список случайно упорядоченных элементов (выделяя для них память). Функция showlist выводит ключи из этого списка. Программы сортировки используют перегруженную операцию < для сравнения элементов и работы с указателями при упорядочении элементов. Представление данных для узлов реализовано обычным способом (см. "Элементарные структуры данных" ) и включает конструктор узлов, который заполняет каждый новый узел заданным значением и пустой ссылкой.
struct node
{ Item item; node* next;
node(Item x)
{ item = x; next = 0; }
};
typedef node *link;
link randlist(int);
link scanlist(int&);
void showlist(link); link sortlist(link);
Программа 6.15 — это низкоуровневый интерфейс, в котором нет различий между ссылкой (указателем на узел) и связным списком (указатель, который либо равен 0, либо указывает на узел, содержащий указатель на список). Конечно, для списков и реализаций можно было бы выбрать АТД первого класса, который в точности определяет все соглашения по фиктивным узлам и т.д. Однако мы выбрали низкоуровневый подход, поскольку он позволяет больше сосредоточиться на работе со ссылками, которые характеризуют сами алгоритмы и структуры данных — ведь именно они являются предметом изучения настоящей книги.
Существует фундаментальное правило, которое касается работы со связными структурами и критично для многих приложений, но не всегда четко просматривается в наших кодах. В более сложных средах указатели на узлы списка, с которыми мы работаем, могут изменяться другими частями прикладной системы (т.е., они принадлежат мультиспискам). Тот факт, что на узлы, к которым мы обращаемся через указатели, могут влиять части приложения вне программы сортировки, означает, что наши программы могут менять в узлах только ссылки и не должны изменять ключи или другую информацию. Например, если нужно выполнить обмен, то вроде бы проще обменять значения элементов (что мы и делали при сортировке массивов). Но в таком случае любое обращение к любому из этих узлов по какой-то другой ссылке обнаружит, что значение изменилось, а это недопустимо. Необходимо изменить только ссылки таким образом, чтобы при просмотре списка по доступным нам ссылкам узлы были упорядочены, но чтобы сохранился прежний порядок при обращениях по любым другим ссылкам. Реализации при этом усложняются, но обычно это необходимо.
Для работы со связными списками можно приспособить сортировку вставками, сортировку выбором и пузырьковую сортировку, хотя в каждом случае возникают интересные проблемы. Сортировка выбором реализуется достаточно просто: имеется входной список (в котором находятся исходные данные) и выходной список (в котором собирается результат сортировки), и выполняются просмотры списка, чтобы найти максимальный элемент, который затем удаляется из входного списка и помещается в начало выходного (см. рис. 6.16). Реализация этой операции является несложным упражнением по обработке связных списков и представляет собой полезный метод сортировки коротких списков. Эта реализация приведена в программе 6.16. Другие методы оставлены для проработки в качестве упражнений.
На этой диаграмме показан один шаг сортировки выбором связного списка. Имеется входной список, на который указывает h->next, и выходной список, на который указывает out (вверху). Входной список просматривается так, чтобы t указывал на узел, содержащий максимальный элемент, а max указывал на предшествующий узел. Эти указатели необходимы для исключения t из входного списка (с уменьшением его длины на 1) и помещения его в начало выходного списка (с увеличением его длины на 1), сохраняя упорядоченность выходного списка (внизу). Процесс завершается, когда будет исчерпан весь входной список, а выходной список будет содержать упорядоченные элементы.
Программа 6.16. Сортировка выбором связного списка
Сортировка выбором связного списка достаточно проста, но несколько отличается от сортировки массива тем же методом, поскольку помещение элемента в начало списка выполняется проще. Используются входной список (на него указывает h->next) и выходной список (на который указывает out). Если входной список не пуст, выполняется его просмотр, чтобы найти максимальный элемент, который затем удаляется из входного и помещается в начало выходного списка. В данной реализации используется вспомогательная подпрограмма findmax, возвращающая ссылку на узел, ссылка которого указывает на максимальный элемент в списке (см. упражнение 3.34).
link listselection(link h)
{ node dummy(0); link head = &dummy, out = 0;
head->next = h;
while (head->next != 0)
{ link max = findmax(head), t = max->next;
max->next = t->next;
t->next = out; out = t;
}
return out;
}
В некоторых задачах обработки списков вообще нет необходимости в явной реализации сортировки. Например, мы решили всегда поддерживать упорядоченность списка и включать новые узлы в список как при сортировке вставками. Такой подход требует незначительных дополнительных затрат, если вставки производятся сравнительно редко, либо если список имеет небольшие размеры, а также в ряде других случаев. Например, перед вставкой новых узлов может понадобиться по какой-то другой причине просмотреть весь список (возможно, чтобы убедиться в отсутствии дубликатов). В "Хеширование" нам встретится алгоритм, который использует упорядоченные связные списки, а в "Таблицы символов и деревья бинарного поиска" и "Хеширование" будут рассмотрены многочисленные структуры данных, эффективность которых достигается благодаря наличию порядка.
Упражнения
6.64. Приведите содержимое входного и выходного списков при упорядочении программой 6.15 ключей A S O R T I N G E X A M P L E.
6.65.разрабо тайтереализациюинтерфейсадлятипасвязно го списка,приведенно го впро грамме6.15.
6.66. Напишите клиентскую программу-драйвер для вызова программ сортировки связных списков (см. упражнение 6.9).
6.67. Разработайте АТД первого класса для связных списков (см. раздел 4.8 "Абстрактные типы данных" ), который включает конструктор для инициализации случайными значениями, конструктор для инициализации с помощью перегруженной операции <<, вывод данных с помощью перегруженной операции >>, деструктор, конструктор копий и функцию-член sort. Для реализации функции sort используйте алгоритм сортировки выбором с приватной функцией-членом findmax.
6.68. Напишите реализацию пузырьковой сортировки для связных списков. Внимание: обмен местами двух соседних элементов в связном списке — более сложная операция, чем может показаться на первый взгляд.
6.69. Оформите программу сортировки вставками 3.11 таким образом, чтобы она обладала теми же возможностями, что и программа 6.16.
6.70. Для некоторых входных файлов вариант сортировки вставками, использованный в программе 3.11, выполняет сортировку связных списков значительно медленнее, чем сортировку массивов. Опишите один из таких файлов и объясните, в чем заключается проблема.
6.71. Напишите реализацию варианта сортировки Шелла для связных списков, которая не потребует существенно большего объема памяти или времени при сортировке больших случайно упорядоченных файлов, нежели вариант для сортировки массивов. Совет: используйте пузырьковую сортировку.
6.72. Реализуйте АТД для последовательностей, который позволит использовать одну и ту же клиентскую программу для отладки реализаций сортировки как связных списков, так и массивов. То есть клиентские программы должны иметь возможность генерировать последовательности из N элементов (случайно сгенерированных или из стандартного ввода), сортировать последовательности и выводить их содержимое. Например, АТД в файле SEQ.cxx должен работать со следующим программным кодом:
#include "Item.h"
#include "SEQ.cxx"
main(int argc, char *argv[])
{ int N = atoi(argv[1], sw = atoi(argv[2]);
if (sw) SEQrand(N); else SEQscan();
SEQsort();
SEQshow();
}
Напишите одну реализацию, в которой используется представление в виде массива, и другую, где используется представление в виде связного списка. Воспользуйтесь сортировкой выбором.
6.73. Расширьте реализацию из упражнения 6.72 так, чтобы она стала АТД первого класса. Совет: поищите решение в библиотеке стандартных шаблонов.
Метод распределяющего подсчета
Некоторые алгоритмы сортировки достигают повышения эффективности, используя особые свойства ключей. Вот, например, такая задача: требуется выполнить сортировку файла из N элементов, ключи которых принимают различные значения в диапазоне от 0 до N — 1. Эту проблему можно решить одним оператором, если воспользоваться временным массивом b:
for (i = 0; i < N; i++) b[key(a[i])] = a[i];
Здесь ключи используются как индексы, а не как абстрактные элементы, которые можно только сравнивать друг с другом. В этом разделе мы ознакомимся с элементарным методом, который использует индексацию по ключам для повышения эффективности сортировки, если ключами служат целые числа из небольшого диапазона.
Если все ключи равны 0, то сортировка тривиальна. Теперь предположим, что возможны два различных значения ключа — 0 и 1. Такая задача может возникнуть, когда требуется выделить элементы файла, удовлетворяющие некоторому (возможно, сложному) критерию: допустим, ключ, равный 0, означает, что элемент следует " принять " , а равный 1 — что элемент должен быть " отвергнут " . Один из способов сортировки состоит в том, что сначала подсчитывается количество нулевых ключей, затем выполняется второй подход по исходному массиву a, распределяющий его элементы во временном массиве b. Для этого используется массив из двух счетчиков. Вначале в cnt[0] заносится 0, а в cnt[1] — количество нулевых ключей в файле. Это означает, что в исходном файле нет ключей, меньших 0, и имеется cnt[1] ключей, меньших 1. Понятно, что массив b можно заполнить следующим образом: в начало массива записываются нулевые ключи (начиная с b[[cnt[0]], т.е. с b[0]), а потом единичные, начиная с b[cnt[1]]. Таким образом, код
for (i = 0; i < N; i++) b[cnt[a[i]]++] = a[i];
правильно распределяет элементы из a в массиве b. Здесь опять ускорение сортировки достигается за счет использования ключей в качестве индексов (для выбора между cnt[0] и cnt[1]).
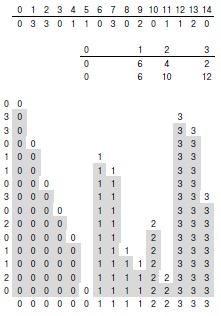
Этот подход нетрудно распространить на общий случай. Ведь чаще встречается подобная, но более реальная задача: отсортировать файл, состоящий из N элементов, ключи которого принимают целые значения в диапазоне от 0 до M — 1. Базовый метод, описанный в предыдущем параграфе, можно расширить до алгоритма, получившего название распределяющего подсчета (key-indexed counting), который эффективно решает эту задачу для не слишком больших M. Как и в случае двух ключей, идея состоит в том, чтобы подсчитать количество ключей с каждым конкретным значением, а затем использовать счетчики для перемещения в соответствующие позиции во время второго прохода по сортируемому файлу. Сначала подсчитывается число ключей для каждого значения, а затем вычисляются частичные суммы, эквивалентные количеству ключей, меньших или равных каждому такому значению. Далее, как и в случае двух значений ключа, эти числа используются как индексы при распределении ключей. Для каждого ключа величина связанного с ним счетчика рассматривается как индекс, указывающий на конец блока ключей с тем же значением. Этот индекс используется при размещении ключей в массиве b, после чего выполняется его сдвиг на одну позицию вправо. Описанный процесс изображен на рис. 6.17, а реализация приведена в программе 6.17.
Сначала для каждого значения определяется количество ключей в файле, имеющих это значение. В данном примере имеется шесть значений 0, четыре значения 1, два значения 2 и три значения 3. Затем подсчитываются частичные суммы, т.е. количества ключей со значениями меньше данного значения: 0 ключей меньше 0, 6 ключей меньше 1, 10 ключей меньше 2 и 12 ключей меньше 3 (таблица в середине). Потом эти частичные суммы используются в качестве индексов для записи ключей в соответствующие позиции: 0 из начала файла помещается в позицию 0, после чего указатель для 0 увеличивается на единицу и указывает на позицию, куда будет записан следующий 0. Затем 3 из следующей позиции исходного файла помещается в позицию 12 (поскольку в файле имеются 12 ключей со значением, меньшим 3), и соответствующий счетчик увеличивается на 1, и т.д.
Лемма 6.12. Метод распределяющего подсчета представляет собой сортировку с линейным временем выполнения при условии, что диапазон, в котором находятся значения ключей, превышает размер файла не более чем в постоянное количество раз.
Каждый элемент перемещается дважды: один раз в процессе распределения и один раз при возврате в исходный файл; обращение к каждому ключу также выполняется дважды: один раз при подсчете, другой раз во время распределения. Два других цикла for в алгоритме используются при накоплении счетчиков и несущественно влияют на время выполнения, если количество счетчиков существенно не превосходит размер файла. 
При сортировке очень больших файлов вспомогательный файл b может привести к проблеме нехватки памяти. Программу 6.17 можно изменить так, чтобы она выполняла сортировку на месте (т.е., без необходимости построения вспомогательного файла), используя метод, похожий на применяемый в программе 6.14. Эта операция тесно связана с базовыми методами, которые будут рассматриваться в "Быстрая сортировка" и 10, так что мы отложим ее изучение до упражнений 12.16 и 12.17 из раздела 12.3 "Таблицы символов и деревья бинарного поиска" . Как будет показано в "Таблицы символов и деревья бинарного поиска" , эта экономия памяти достигается за счет устойчивости алгоритма, из-за чего область применения этого алгоритма существенно сужается. Ведь в приложениях, использующих большое количество повторяющихся ключей, часто используются другие ключи, относительный порядок которых должен быть сохранен. Исключительно важный пример такого приложения приведен в "Поразрядная сортировка" .
Программа 6.17. Распределяющий подсчет
Первый цикл for выполняет начальное обнуление всех счетчиков. Второй цикл for подсчитывает во втором счетчике количество 0, в третьем счетчике — количество 1 и т.д. Третий цикл for складывает все эти числа, после чего каждый счетчик содержит количество ключей, меньших или равных соответствующему ключу. Теперь эти числа представляют собой индексы концов тех частей результирующего файла, к которым эти ключи принадлежат. Четвертый цикл for перемещает ключи во вспомогательный массив b в соответствии со значениями этих индексов, а последний цикл возвращает отсортированный файл в файл a. Для работы этого кода необходимо, чтобы ключи были целыми значениями, не превышающими M, хотя его можно легко изменить так, чтобы извлекать ключи из элементов с более сложной структурой (см. упражнение 6.77).
void distcount(int a[], int l, int r)
{ int i, j, cnt[M];
static int b[maxN];
for (j = 0; j < M; j + +) cnt[j] = 0;
for (i = l; i <= r; i++) cnt[a[i]+1]+ + ;
for (j = 1; j < M; j + +) cnt[j] += cnt[j-1];
for (i = l; i <= r; i++) b[cnt[a[i]]++] = a[i];
for (i = l; i <= r; i++) a[i] = b[i];
}
Упражнения
6.74. Напишите специализированную версию метода распределяющего подсчета для сортировки файлов, элементы которых могут принимать только одно из трех значений (a, b или c).
6.75. Предположим, что выполняется сортировка вставками случайно упорядоченного файла, элементы которого принимают одно из трех возможных значений. Каков порядок времени выполнения сортировки: линейный, квадратичный или где-то между ними?
6.76. Покажите процесс сортировки файла A B R A C A D A B R A методом распределяющего подсчета.
6.77. Реализуйте сортировку распределяющим подсчетом для элементов, которые представляют собой потенциально большие записи с целочисленными ключами из небольшого диапазона.
6.78. Реализуйте сортировку распределяющим подсчетом в виде сортировки указателей.