|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Элементарные методы сортировки
Пузырьковая сортировка
Многие начинают знакомство с сортировкой с исключительно простого метода пузырьковой сортировки (bubble sort). В процессе своей работы она выполняет проходы по файлу с обменом местами соседних элементов, нарушающих порядок, до тех пор, пока файл не станет отсортирован. Основным достоинством пузырьковой сортировки является легкость ее реализации, хотя в этом она сравнима с методом вставок и методом выбора. В общем случае пузырьковый метод работает медленнее, однако мы рассмотрим его для полноты картины.
Предположим, что мы всегда передвигаемся по файлу справа налево. Когда на первом проходе попадается минимальный элемент, он меняется местами с каждым элементом слева от него, пока не займет место на левом краю массива. Затем на втором проходе на свою позицию попадает второй по величине элемент и т.д. Значит, для полной упорядоченности файла достаточно выполнить N проходов. Пузырьковую сортировку можно рассматривать как разновидность сортировки выбором, хотя она затрачивает больше работы для помещения каждого элемента в нужную позицию. Программа 6.4 представляет собой реализацию этого алгоритма, а на рис. 6.4 показан пример его работы.
Программа 6.4. Пузырьковая сортировка
Для каждого i от l до r-1 внутренний цикл (j) по элементам a[i], ..., a[r] помещает минимальный элемент в a[i], перебирая элементы справа налево и выполняя сравнение с обменом соседних элементов. Наименьший элемент перемещается при всех таких сравнениях и " всплывает " в начало файла. Как и в сортировке выбором, индекс i перемещается по файлу слева направо, а элементы слева от него находятся в окончательных позициях.
template <class Item>
void bubble(Item a[], int l, int r)
{ for (int i = l; i < r; i++)
for (int j = r; j > i; j-- )
compexch(a[j-1], a[j]);
}
Быстродействие программы 6.4 можно повысить, тщательно оптимизировав внутренний цикл примерно так же, как это было сделано в разделе 6.3 для сортировки вставками (см. упражнение 6.25). В самом деле, сравните коды: программа 6.4 практически идентична неадаптивной сортировке вставками из программы 6.1. Они отличаются только тем, что в сортировке вставками внутренний цикл for перебирает левую (отсортированную) часть массива, а в пузырьковой сортировке — правую (не обязательно упорядоченную) часть массива.
Программа 6.4 использует только инструкции compexch и поэтому не является адаптивной, однако можно повысить ее эффективность для почти упорядоченных файлов, проверяя после каждого прохода, были ли выполнены перестановки (т.е. файл полностью отсортирован, и можно выйти из внешнего цикла). Это усовершенствование ускоряет пузырьковую сортировку на некоторых типах файлов, однако, как будет показано в разделе 6.5, в общем случае оно все равно не так эффективно, как выход из внутреннего цикла сортировки вставками.
В пузырьковой сортировке ключи с малыми значениями постепенно сдвигаются влево. Поскольку проходы выполняются справа налево, каждый ключ меняется местами с ключом слева до тех пор, пока не будет обнаружен ключ с меньшим значением. На первом проходе E меняется местами с L, P и M и останавливается справа от A; затем A продвигается к началу файла, пока не остановится перед другим A, который уже находится на свом месте. Как и в случае сортировки выбором, после i-го прохода i-й по величине ключ устанавливается в окончательное положение, но при этом другие ключи также приближаются к своим окончательным позициям.
Упражнения
6.20. Покажите в стиле рис. 6.4 процесс упорядочения файла E A S Y Q U E S T I O N методом пузырьковой сортировки.
6.21. Приведите пример файла, для которого пузырьковая сортировка выполняет максимально возможное количество перестановок элементов.
6.22. Является ли пузырьковая сортировка устойчивой?
6.23. Объясните, почему пузырьковая сортировка лучше неадаптивной версии сортировки выбором, описанной в упражнении 6.19.
6.24. Экспериментально определите количество сэкономленных проходов для случайных файлов из N элементов, если добавить в пузырьковую сортировку проверку упорядоченности файла.
6.25. Разработайте эффективную реализацию пузырьковой сортировки с минимально возможным числом операторов во внутреннем цикле. Проверьте, что ваши " усовершенствования " не снижают быстродействие программы!
Характеристики производительности элементарных методов СОРТИРОВКИ
Сортировка выбором, сортировка вставками и пузырьковая сортировка являются квадратичными по времени алгоритмами как в худшем, так и в среднем случае; все они не требуют дополнительной памяти. Поэтому время их выполнения отличается лишь на постоянный коэффициент, хотя принципы работы существенно различаются (см. рис. 6.5, рис. 6.6 и рис. 6.7).
Эти снимки процесса сортировки вставками (слева) и выбором (справа) случайной последовательности иллюстрируют выполнение сортировки обоими методами. Упорядоченность массива показана в виде графика зависимости a[i] от индекса i. Перед началом сортировки график представляет равномерно распределенную случайную величину, а по окончании сортировки он выглядит диагональю из левого нижнего угла в правый верхний угол. Сортировка вставками никогда не забегает вперед за текущую позицию в массиве, а сортировка выбором никогда не возвращается назад.
На этой диаграмме показаны различия в способах упорядочения файла сортировкой вставками, сортировкой выбором и пузырьковой сортировкой. Сортируемый файл представлен отрезками, которые сортируются по углу наклона. Черные отрезки означают элементы, к которым выполнялся доступ на каждом проходе сортировки; серые отрезки означают не задействованные элементы. В процессе сортировки вставками (слева) вставляемый элемент перемещается на каждом проходе примерно на полпути назад по упорядоченной части. Сортировка выбором (в центре) и пузырьковая сортировка (справа) перебирают на каждом проходе всю неотсортированную часть массива, чтобы найти в ней следующий наименьший элемент. Различие между этими методами заключается в том, что пузырьковая сортировка меняет местами каждую попавшуюся неупорядоченную пару соседних элементов, а сортировка выбором сразу помещает минимальный элемент в окончательную позицию. Это различие проявляется в том, что по мере выполнения пузырьковой сортировки неотсортированная часть массива становится все более упорядоченной.
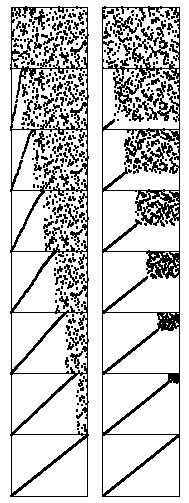
Стандартная пузырьковая сортировка (слева) похожа на сортировку выбором тем, что на каждом проходе один элемент занимает свою окончательную позицию, но одновременно она асимметрично привносит упорядоченность в остальную часть массива. Поочередная смена направления просмотра массива (т.е. просмотр от начала до конца массива меняется на просмотр от конца до начала и наоборот) дает новую разновидность пузырьковой сортировки, получившей название шейкерной сортировки (справа), которая заканчивается быстрее (см. упражнение 6.30).
В общем случае время выполнения алгоритма сортировки пропорционально количеству операций сравнения, выполняемых этим алгоритмом, количеству перемещений или обменов элементов, а, возможно, и тому, и другому сразу. Для случайно упорядоченных данных сравнение элементарных методов сортировки сводится к изучению постоянных коэффициентов, на которые отличаются количества выполняемых операций сравнений и обменов, а также постоянных коэффициентов, на которые отличаются длины внутренних циклов. В случае входных данных с особыми характеристиками времена выполнения различных видов сортировок могут отличаться и более чем на постоянный коэффициент. В данном разделе будут подробно рассмотрены аналитические результаты, на которых основано это заключение.
Лемма 6.1. Сортировка выбором выполняет порядка N2/ 2 сравнений и N обменов элементов.
Данное свойство легко проверить на примере данных, приведенных на
рис.
6.2. Это таблица размером N х N, в которой незаштрихованные буквы соответствуют сравнениям. Примерно половина элементов этой таблицы не заштрихована, эти элементы расположены над диагональю. Каждый из N — 1 элементов на диагонали (кроме последнего) соответствует операции обмена. Точнее, исследование кода показывает, что для каждого i от 1 до N — 1 выполняется один обмен и N — i сравнений, так что всего выполняется N — 1 операций обмена и (N — 1) + (N — 2) + ... + 2 + 1 = N (N — 1) / 2 операций сравнения. Эти соображения не зависят от природы входных данных; единственная часть сортировки выбором, которая зависит от характера входных данных — это количество присваиваний переменной min новых значений. В худшем случае эта величина может оказаться квадратичной, однако в среднем она имеет порядок O (N logN) (см. раздел ссылок), поэтому можно сказать, что время выполнения сортировки выбором не чувствительно к природе входных данных. 
Лемма 6.2. Сортировка вставками выполняет в среднем порядка N2/ 4 сравнений и N2/ 4 полуобменов (перемещений), а в худшем случае в два раза больше.
Сортировка, реализованная в программе 6.3, выполняет одинаковое количество сравнений и перемещений. Как и в случае леммы 6.1, эту величину легко наглядно увидеть на диаграмме размером N х N, которая демонстрирует подробности работы алгоритма (см.
рис.
6.3). Здесь ведется подсчет элементов под главной диагональю — в худшем случае всех. Для случайно упорядоченных входных данных можно ожидать, что каждый элемент проходит в среднем примерно половину пути назад, поэтому необходимо учитывать только половину элементов, лежащих ниже диагонали. 
Лемма 6.3. Пузырьковая сортировка выполняет порядка N2/ 2 сравнений и N2/ 2 обменов — как в среднем, так и в худшем случае.
На i-ом проходе пузырьковой сортировки нужно выполнить N — i операций сравнения-обмена, поэтому лемма доказывается так же, как и случае сортировки выбором. Если алгоритм усовершенствован так, что его выполнение прекращается при обнаружении упорядоченности файла, то время его выполнения зависит от входных данных. Если файл уже отсортирован, то достаточно лишь одного прохода, однако в случае обратной упорядоченности i-й проход требует выполнения N— i сравнений и обменов. Как отмечалось ранее, производительность сортировки для обычных данных ненамного выше, чем для худшего случая, однако доказательство этого факта достаточно сложно (см. раздел ссылок). 
Хотя понятие частично отсортированного файла по своей природе довольно неточно, сортировка вставками и пузырьковая сортировка хорошо работают с файлами, не обладающими произвольной организацией, которые довольно часто встречаются на практике. Применение в таких случаях универсальных методов сортировки нецелесообразно. Например, рассмотрим выполнение сортировки вставками для уже упорядоченного файла. Для каждого элемента сразу выясняется, что он находится на своем месте, и общее время выполнения оказывается линейным. Это же справедливо и в отношении пузырьковой сортировки, однако для сортировки выбором трудоемкость остается квадратичной.
Определение 6.2. Инверсией называется пара ключей, которые нарушают порядок в файле.
Для подсчета количества инверсий в файле необходимо для каждого элемента просуммировать число элементов слева, которые больше его (мы будем называть это значение количеством инверсий, соответствующих данному элементу). Но это число есть в точности расстояние, на которое должны переместиться элементы во время сортировки вставками. В частично отсортированном файле меньше инверсий, чем в произвольно упорядоченном файле.
Существуют такие типы частично отсортированных файлов, в которых каждый элемент находится близко к своей окончательной позиции. Например, некоторые игроки сортируют имеющиеся у них на руках карты, сначала группируя их по мастям — тем самым помещая близко к окончательным позициям — а затем упорядочивают карты каждой масти по старшинству. Далее мы рассмотрим ряд методов сортировки, которые работают примерно так же: на начальных этапах они размещают элементы вблизи окончательных позиций, в результате чего образуется частично упорядоченный файл, где каждый элемент расположен недалеко от той позиции, которую он должен занять в конечном итоге. Сортировка вставками и пузырьковая сортировка (но не сортировка выбором) эффективно сортируют такие файлы.
Лемма 6.4. Сортировка вставками и пузырьковая сортировка выполняют линейное количество сравнений и обменов в файлах с не более чем постоянным числом инверсий, приходящихся на каждый элемент.
Как было только что сказано, время выполнения сортировки вставками прямо пропорционально количеству инверсий в сортируемом файле. Для пузырьковой сортировки (здесь имеется в виду программа 6.4, где выполнение прекращается, как только файл становится упорядоченным) доказательство требует более тонких рассуждений (см. упражнение 6.29). Для любого элемента каждый проход пузырьковой сортировки уменьшает количество элементов справа, меньших его, в точности на 1 (если оно не было равным 0). Следовательно, для рассматриваемых типов файлов пузырьковая сортировка выполняет не более чем постоянное количество проходов, а значит, количество сравнений и обменов не более чем линейно. 
Наиболее часто встречаются другие виды частично упорядоченных файлов, когда к уже отсортированному файлу добавляются нескольких элементов, либо в сортированном файле изменены ключи нескольких элементов. Для таких файлов наиболее эффективна сортировка вставками; сортировка выбором и пузырьковая сортировка не так эффективны.
Для файлов небольших размеров сортировка вставками и сортировка выбором работают примерно в два раза быстрее пузырьковой сортировки, однако время выполнения любого из этих видов квадратично зависит от размера файла (если размер файла увеличивается в 2 раза, то время его сортировки возрастает в 4 раза). Ни один из этих методов не следует использовать для сортировки больших случайно упорядоченных файлов — например, для сортировки Шелла (см. раздел 6.6) показатели, соответствующие приведенным в таблице, не превышают 2. При большой трудоемкости сравнений — например, когда ключи представлены в виде строк — сортировка вставками работает гораздо быстрее, чем два других способа, т.к. в ней выполняется гораздо меньше сравнений. Здесь не рассмотрена ситуация, когда трудоемкими являются операции обмена; в таких случаях лучшей является сортировка выбором.
| N | 32-разрядные целочисленные ключи | Строковые ключи | ||||||
|---|---|---|---|---|---|---|---|---|
| S | I* | I | B | B* | S | I | B | |
| 1000 | 5 | 7 | 4 | 11 | 8 | 13 | 8 | 19 |
| 2000 | 21 | 29 | 15 | 45 | 34 | 56 | 31 | 78 |
| 4000 | 85 | 119 | 62 | 182 | 138 | 228 | 126 | 321 |
Обозначения:
| S | Сортировка выбором (программа 6.2) |
| I* | Сортировка вставками на основе операций обмена (программа 6.1) |
| I | Сортировка вставками (программа 6.3) |
| B | Пузырьковая сортировка (программа 6.4) |
| B* | Шейкерная сортировка (упражнение 6.30) |
Лемма 6.5. Сортировка вставками использует линейное количество сравнений и обменов для файлов с не более чем постоянным количеством элементов, которые имеют более чем постоянное число соответствующих инверсий.
Время выполнения сортировки вставками зависит от общего числа инверсий в файле и не зависит от характера распределения этих инверсий в файле. 
Чтобы сделать выводы о времени выполнения на основании лемм 6.1—6.5, необходимо проанализировать относительную стоимость операций сравнения и обмена, а этот фактор, в свою очередь, зависит от размера элементов и ключей (см. таблицу 6.1). Например, если элементы представляют собой ключи из одного слова, то операция обмена (требующая четырех доступов к массиву) должна быть в два раза более трудоемкой, чем операции сравнения. В такой ситуации время выполнения сортировки вставками и сортировки выбором примерно соизмеримы, а пузырьковая сортировка работает медленнее. Но если элементы гораздо больше ключей, то лучшей является сортировка выбором.
Лемма 6.6. Время выполнения сортировки выбором линейно для файлов с большими элементами и малыми ключами.
Пусть M — отношение размера элемента к размеру ключа. Тогда можно предположить, что сравнение выполняется за 1 единицу времени, а обмен — за M единиц времени. Сортировка выбором затрачивает на операции сравнения порядка
N2/ 2
единиц времени и порядка NM единиц времени на операции обмена. Если M больше постоянного кратного N, то произведение NM превосходит N2, поэтому время выполнения сортировки пропорционально произведению NM, которое, в свою очередь, пропорционально времени, необходимому для перемещения всех данных. 
Пусть, например, требуется отсортировать 1000 элементов, каждый из которых состоит из ключа длиной 1 слово и данных длиной 1000 слов, и нужно фактически переупорядочить эти элементы. Тогда трудно найти что-либо лучше сортировки выбором, поскольку время выполнения будет в основном определяться стоимостью перемещения всего миллиона слов данных. В разделе 6.8 будут рассмотрены альтернативы переупоря-дочиванию данных.
Упражнения
6.26. Какой из трех элементарных методов (сортировка выбором, сортировка вставками и пузырьковая сортировка) выполняется быстрее для файла со всеми одинаковыми ключами?
6.27. Какой из трех элементарных методов выполняется быстрее для файла, упорядоченного по убыванию?
6.28. Приведите пример файла из 10 элементов (используйте ключи от A до J), в процессе сортировки которого пузырьковая сортировка выполняет меньше сравнений, чем метод вставок — либо докажите, что такой файл не существует.
6.29. Покажите, что для любого элемента каждый проход пузырьковой сортировки уменьшает количество элементов слева, больших его, в точности на 1 (если оно не было равно 0).
6.30. Реализуйте вариант пузырьковой сортировки, который попеременно выполняет проходы по данным слева направо и справа налево. Этот (более быстродействующий, но и более сложный) алгоритм называется шейкерной сортировкой (shaker sort) .
6.31. Покажите, что лемма 6.5 не выполняется для шейкерной сортировки (см. упражнение 6.30).
6.32. Реализуйте сортировку выбором на PostScript (см. раздел 4.3 "Абстрактные типы данных" ) и воспользуйтесь полученной реализацией для построения рисунков вида 6.5—6.7. Можно применить рекурсивную реализацию или прочитать в руководстве по PostScript о циклах и массивах.