Элементарные методы сортировки

Сортировка индексов и указателей

Разработка реализации типа данных строки, наподобие программ 6.9 и 6.10, представляет особый интерес, поскольку строки символов широко используются как ключи сортировки. Строки могут иметь различные длины, в том числе и очень большие, поэтому создание, удаление и сравнение строк могут потребовать значительных затрат, и следует проявить особую осторожность, чтобы в реализации не было излишних операций этого вида.

С этой целью мы применяем такое представление данных, которое состоит из указателя (на массив символов) — стандартное представление строки в стиле языка С. А первая строка программы 6.9 изменяется на

typedef struct { char *str; } Item;
      

что превращает ее в интерфейс для строк. Указатель помещается в структуру потому, что C++ не позволяет перегружать операцию < для встроенных типов, к которым относятся указатели. Подобные ситуации не являются чем-то необычным в C++: класс (или структура), который приспосабливает интерфейс для другого типа данных, называется классом-оболочкой (wrapper class). В данном случае мы не требуем от класса-оболочки слишком многого, но в некоторых случаях возможны более сложные реализации. Вскоре будет рассмотрен еще один пример.

Программа 6.11 представляет собой реализацию для строковых элементов. Перегружен ная операция < легко реализуется с помощью функции сравнения строк из библиотеки С, но реализовать функцию scan (и rand) труднее, поскольку нужно учитывать распределение памяти для строк. Программа 6.11 использует метод, который был рассмотрен в "Элементарные структуры данных" (программа 3.17) — использование буфера в реализации типа данных. Другие варианты — динамическое выделение памяти для каждой строки, использование реализации класса вроде класса String из библиотеки стандартных шаблонов, либо использование буфера в клиентской программе. Для сортировки строк символов можно воспользоваться любым из этих подходов (с соответствующими интерфейсами), используя любую реализацию сортировки из рассмотренных нами.

Мы сталкиваемся с необходимостью подобного управления памятью всякий раз, когда разбиваем программу на модули. Кто будет отвечать за управление памятью, соответствующее конкретной реализации какого-то объекта — клиентская программа, реализация типа данных или система? На этот вопрос нет готового однозначного ответа (хотя некоторые разработчики языков программирования являются ярыми приверженцами одного из вариантов). В некоторых современных системах программирования (включая некоторые реализации С++) имеются встроенные механизмы автоматического управления памятью. Мы еще вернемся к этому вопросу в "Очереди с приоритетами и пирамидальная сортировка" , при обсуждении реализации более сложных абстрактных типов данных.

Программа 6.11 представляет собой пример сортировки указателей (pointer sort), и мы вскоре рассмотрим этот принцип в более общем виде. Другой простой подход к сортировке без (непосредственных) перемещений элементов заключается во введении индексного массива, когда доступ к ключам элементов выполняется только для их сравнения.

Программа 6.11. Реализация типа данных для строковых элементов

Эта реализация позволяет упорядочивать строки в стиле языка С, используя наши программы сортировки. Для представления данных используется структура, которая содержит указатель на символ (см. в тексте), благодаря чему сортировка выполняется для массива указателей на символы, переупорядочивая их таким образом, что строки, на которые они указывают, выстраиваются в алфавитно-цифровом порядке. Чтобы наглядно продемонстрировать процесс управления памятью, здесь определен буфер памяти фиксированного размера, где хранятся символы строк; наверно, удобнее было бы динамическое распределение памяти. Реализация функции rand опущена.

#include <iostream.h>
#include <stdlib.h>
#include <string.h>
#include "Item.h"
static char buf[100000];
static int cnt = 0;
int operator<(const Item& a, const Item& b)
  { return strcmp(a.str, b.str) < 0; }
void show(const Item& x)
  { cout << x.str << " "; }
int scan(Item& x)
  { int flag = (cin >> (x.str = &buf[cnt])) != 0;
    cnt += strlen(x.str)+1;
    return flag;
  }
      

Предположим, что сортируемые элементы находятся в массиве data[0], ..., data[N-1], и по каким-то причинам мы не хотим перемещать их (возможно, из-за огромных размеров). Тогда для упорядочения используется второй массив а с индексами сортируемых элементов. Первоначально его элементы a[i] инициализируются значениями i для i = 0, ..., N-1. То есть вначале a[0] содержит индекс первого элемента данных, a[1] — второго элемента данных и т.д. А сама сортировка сводится к такому переупорядочению массива индексов, что a[0] будет содержать индекс элемента данных с наименьшим значением ключа, a[1] — индекс следующего элемента данных с минимальным значением ключа и т.д. Тогда эффект упорядочения достигается доступом к ключам через индексы — например, так можно вывести массив в порядке возрастания его ключей.

В этом случае нужно указать, что сортировка выполняет упорядочивание индексов массива, а не просто целых чисел. Тип Index следует определить так, чтобы можно было перегрузить операцию < следующим образом:

int operator<(const Index& i, const Index& j)
  { return data[i] < data[j]; }
      

Теперь при наличии массива a объектов типа Index любая из наших функций сортировки переупорядочит индексы в массиве a так, что значение a[i] будет равно числу ключей, меньших, чем ключ элемента data[i] (индекс a[i] в отсортированном массиве). (Для простоты здесь предполагается, что данные представляют собой просто ключи, а не элементы в полном объеме; этот принцип можно распространить на более крупные и сложные элементы — нужно лишь изменить операцию < для доступа конкретно к ключам таких элементов, либо воспользоваться функцией-членом класса для вычисления ключей.) Для определения типа Index используется класс-оболочка:

struct intWrapper
  {
    int item;
    intWrapper(int i = 0)
      { item = i; }
    operator int() const
      { return item; }
  };
  type def intWrapper Index;
      

Конструктор в данной структуре преобразует любое значение типа int в Index, а операция приведения типа int() преобразует любое значение Index обратно в int — значит, объекты типа Index можно использовать везде, где возможно применение объектов встроенного типа int.

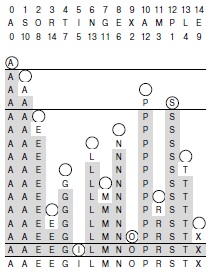
Пример индексации, где одни и те же элементы сортируются по двум различным ключам, представлен на рис. 6.14. Одна клиентская программа может определить операцию < для работы с одним ключом, а другая — для использования другого ключа, но обе они могут воспользоваться одной и той же программой сортировки для построения массива индексов, который обеспечит доступ к элементам в порядке возрастания их ключей.

Рис. 6.14. Пример индексной сортировки

Работая с индексами, а не с самими записями, можно упорядочить массив одновременно по нескольким ключам. В этом примере данные могут быть фамилиями студентов и их оценками, второй столбец представляет собой результат индексной сортировки по именам, а третий столбец — результат индексной сортировки по убыванию оценок. Например, Wilson — фамилия, идущая по алфавиту последней, и ей соответствует десятая оценка, а фамилия Adams является первой по алфавиту, и ей соответствует шестая оценка. Переупорядочение N различных неотрицательных целых чисел, меньших N, в математике называется перестановкой, т.е. индексная сортировка выполняет перестановку. В математике перестановки обычно определяются как переупорядочения целых чисел от 1 до N; мы же будем употреблять числа от 0 до N— 1, чтобы подчеркнуть прямую связь между перестановками и индексами массивов в С++.

Такой поход с использованием массива индексов вместо реальных элементов работает в любом языке программирования, который поддерживает массивы. Другая возможность заключается в использовании указателей, как в реализации недавно рассмотренного строкового типа данных (программа 6.11). В случае сортировки массива элементов фиксированного размера сортировка указателей практически эквивалентна индексной сортировке, только к каждому индексу прибавляется адрес массива. Однако сортировка указателей — гораздо более общий вид сортировки, т.к. указатели могут указывать на что угодно, а сортируемые элементы не обязательно должны иметь фиксированный размер. Как и в случае индексной сортировки, если а есть массив указателей на ключи, то результатом вызова функции sort будет такое переупорядочение указателей, что последовательный доступ к ним означает доступ к отсортированным ключам. Операции сравнения реализуются с помощью обращений по указателям, а операции обмена реализуются как обмен указателей.

Функция qsort из стандартной библиотеки C представляет собой сортировку указателей (см. программу 3.17), которая принимает функцию сравнения в качестве аргумента (а не использует перегруженную операцию <, как мы обычно делаем). У этой функции четыре аргумента: массив, количество сортируемых элементов, размер элементов и указатель на функцию, которая выполняет сравнение двух элементов, обращаясь к ним через заданные указатели. Например, если тип Item определен как char*, то приведенный ниже код реализует сортировку строк в соответствии с принятыми нами соглашениями:

int compare (void *i, void *j)
  { return strcmp(*(Item *)i, *(Item *)j); }
void sort (Item a[], int l, int r)
  { qsort(a, r-l+1, sizeof(Item), compare); }
      

В этом интерфейсе не указан работающий алгоритм, хотя на практике широко применяется быстрая сортировка см. "Быстрая сортировка" . В "Быстрая сортировка" мы рассмотрим многие причины, почему это так. В данной главе, а также в главах 7—11, мы постепенно разберемся, почему в некоторых конкретных случаях более удобны другие методы сортировки. Кроме того, мы рассмотрим возможности ускорения вычислений в тех случаях, когда время выполнения сортировки является критическим фактором в приложении.

В обычных приложениях указатели используются для доступа к записям, которые могут иметь несколько ключей. Например, записи, содержащие фамилии студентов с оценками или фамилии людей с их возрастами можно определить следующим образом:

struct record { char[30] name; int num; }
      

Вполне может потребоваться выполнить их сортировку, используя в качестве ключа любое из этих полей. Программы 6.12 и 6.13 могут служить примерами интерфейса и реализации сортировки указателей, которые позволяют сделать это. В них используются массив указателей на записи и различные реализации операции < для различных применений сортировки.

Программа 6.12. Интерфейс типа данных для элементов в виде записей

Записи содержат два ключа: ключ строкового типа (например, фамилия) в первом поле и целое число (например, оценка) — во втором поле. Мы считаем, что эти записи слишком большие, чтобы их копировать, поэтому Item определяется как структура, содержащая указатель на запись.

struct record { char name[30]; int num; };
typedef struct { record *r; } Item;
int operator<(const Item&, const Item&);
void rand(Item&);
void show(const Item&);
int scan(Item&);
      

Программа 6.13. Реализация типа данных для элементов в виде записей

Приведенные ниже реализации функций scan и show для записей работают в стиле реализации строкового типа данных из программы 6.11: они выделяют память для хранения строк и работают с этой памятью. Реализация операции < находится в отдельном файле, чтобы подставлять различные реализации и таким образом менять ключи сортировки без изменения остального кода.

static record data[maxN];
static int cnt = 0;
void show(const Item& x)
  { cout << x.r->name << " " << x.r->num << endl; }
int scan(Item& x)
  {
    x.r = &data[cnt++];
    return (cin >> x.r->name >> x.r->num) != 0;
  }
      

Например, если откомпилировать программу 6.13 вместе с файлом, содержащим код

#include "Item.h"
int operator<(const Item &a, const Item &b)
  { return a.r->num < b.r->num); }
      

то получим тип данных элементов, для которых любая из наших реализаций функции sort выполнит сортировку указателей по целочисленному полю; а если откомпилировать программу 6.13 вместе с файлом, содержащим код

#include "Item.h" include <string.h>
int operator<(const Item &a, const Item &b)
  { return strcmp(a.r->name, b.r->name) < 0; }
      

то получим тип данных элементов, для которых любая из наших реализаций функции sort выполнит сортировку указателей по строковому полю.

Индексы или указатели используются в основном для того, чтобы не перемещать сортируемые данные. Можно " отсортировать " файл, даже если разрешено только его чтение. Более того, используя несколько массивов индексов или указателей, можно сортировать один и тот же файл по нескольким ключам (см. рис. 6.14). Такая возможность обработки данных без их изменения полезна во многих ситуациях.

Другая причина работы с индексами заключается в том, что это позволяет избежать расходов на перемещения записей целиком. В случае больших записей (и маленьких ключей) достигается значительная экономия, поскольку для выполнения сравнения нужен доступ лишь к небольшой части записи, а большая часть записи в процессе сортировки вообще не затрагивается. При таком косвенном подходе стоимость операции обмена примерно равна стоимости операции сравнения в общем случае, когда сравниваются записи произвольной длины (за счет дополнительного объема памяти для индексов или указателей). В самом деле, если ключи длинные, то затраты на обмен могут быть даже меньше, чем на сравнение. При оценке времени выполнения различных методов сортировки файлов целых чисел часто предполагается, что стоимости операций сравнения и обмена примерно одинаковы. Выводы, полученные на основе такого предположения, справедливы для широкого класса приложений, в которых применяется сортировка указателей или индексов.

Во многих случаях нет необходимости физического переупорядочения данных в соответствии с порядком размещения соответствующих индексов, и данные можно выбирать по порядку с помощью индексного массива. Если такой подход почему-то не годится, то возникнет обычная задача классического программирования: каким образом переупорядочить записи файла, если для него выполнена индексная сортировка? Код

for (i=0; i < N; i++) datasorted[i] = data[a[i]];
      

тривиален, однако требует дополнительной памяти, достаточной для размещения еще одной копии массива. А что делать, если для второй копии не хватает места? Ведь нельзя же просто записать data[i] = data[a[i]], ибо тогда предыдущее значение data[i] окажется затертым — вполне возможно, что преждевременно.

На рис. 6.15 показан способ решения этой проблемы за один проход по файлу. Чтобы переместить первый элемент на то место, где он должен быть, мы переносим элемент из этой позиции на его место и т.д. В процессе этих перемещений однажды попадется элемент, который нужно переместить в первую позицию, после чего на своих местах окажется некоторый цикл элементов. Далее мы перейдем ко второму элементу и выполним те же операции для его цикла, и так далее (любые элементы, которые уже находятся в своих окончательных позициях (a[i] = i), принадлежат циклам длиной 1 и не перемещаются).

Рис. 6.15. Обменная сортировка

Чтобы упорядочить массив на месте, мы просматриваем его слева направо, циклически перемещая элементы, которые находятся не на своих местах. Врассмат-риваемом примере имеются четыре цикла, причем первый и последний являются вырожденными циклами из одного элемента. Второй цикл начинается с позиции 1. Элемент S запоминается во временной переменной, оставляя в позиции 1 пустое место. Перемещение второго А приводит к появлению пустого места в позиции 10. Это пустое место заполняется элементом Р, который оставляет пустое место в позиции 12. Это пустое место должно быть заполнено элементом в позиции 1, поэтому туда переносится запомненный элемент S, тем самым завершая цикл 1 10 12, который помещает эти элементы в окончательные позиции. Аналогично выполняется цикл 2 8 6 13 4 7 11 3 14 9, который и завершает сортировку.

Конкретно, для каждого значения i сохраняется значение data[i], и в индексную переменную k заносится значение i. Теперь можно считать позицию i свободной и найти элемент, который должен заполнить это место. Таким элементом является data[a[k]], и операция присваивания data[k] = data[a[k]] перемещает это пустое место в a[k]. Теперь пустое место появилось в позиции data[a[k]], и в k заносится значение a[k]. Повторяя эти действия, мы в конце концов оказываемся в ситуации, когда пустое место должно быть заполнено предварительно сохраненным значением data[i]. Когда мы помещаем элемент в какую-либо позицию, мы вносим соответствующие изменения в массив а. Для любого элемента, который уже занимает свою позицию, a[i] равно i, и вышеописанный процесс сводится к пустой операции. Перемещаясь по массиву и начиная новый цикл всякий раз, когда встречается элемент, который еще не находится на своем месте, мы перемещаем каждый элемент не более одного раза. Программа 6.14 представляет реализацию рассмотренного процесса.

Этот процесс называется перестановкой на месте (in situ permutation) или обменным упорядочением (in-place rearrangement) файла. Отметим еще раз: хотя сам по себе алгоритм весьма интересен, во многих приложениях в нем нет необходимости, ибо вполне достаточно косвенного доступа к элементам. Кроме того, если записи слишком велики относительно их количества, наиболее эффективным может оказаться вариант упорядочения обыкновенной сортировкой выбором (см. лемму 6.5).

Косвенная сортировка требует дополнительной памяти для размещения массива индексов или указателей и дополнительного времени для выполнения косвенных сравнений. Во многих случаях эти затраты являются вполне оправданной ценой за возможность вообще не затрагивать записи. Мы практически всегда будем пользоваться косвенной сортировкой для упорядочивания файлов, состоящих из больших записей, а во многих приложениях часто нет необходимости перемещать сами данные. В этой книге обычно применяется прямой доступ к данным. Однако в некоторых случаях мы будем по уже изложенным причинам использовать массивы индексов или указателей, чтобы не перемещать данные.

Программа 6.14. Обменная сортировка

Массив data[0], ..., data[N-1] должен быть упорядочен на месте в соответствии с массивом индексов a[0], ..., a[N-1]. Любой элемент, для которого a[i] == i, уже находится на своем месте, и с ним ничего не надо делать. Иначе значение data[i] сохраняется в v, и в цикле перемещаются элементы a[i], a[a[i]], a[a[a[i]]] и т.д., пока индекс i не встретится опять. Далее этот процесс повторяется для следующего элемента, который находится не на месте, и все это продолжается в том же духе, пока не будет упорядочен весь файл, причем каждая запись будет перемещена не более одного раза.

template <class Item>
void insitu(Item data[], Index a[], int N)
  { for (int i = 0; i < N; i++)
      { Item v = data[i];
        int j, k;
        for (k = i; a[k] != i; k = a[j], a[j] = j)
{ j = k; data[k] = data[a[k]]; }
        data[k] = v; a[k] = k;
      }
  }
      

Упражнения

6.57. Приведите реализацию типа данных для элементов, которые представляют собой записи, а не указатели на записи. Такая организация данных может оказаться удобной для работы программ 6.12 и 6.13 с небольшими записями. (Учтите, что язык C++ поддерживает присваивание структур.)

6.58. Покажите, как можно использовать функцию qsort для решения задач сортировки, на которые ориентированы программы 6.12 и 6.13.

6.59. Приведите массив индексов, который получается при индексной сортировке ключей E A S Y Q U E S T I O N.

6.60. Приведите последовательность перемещений данных, необходимых для перестановки ключей E A S Y Q U E S T I O N на месте после выполнения индексной сортировки (см. упражнение 6.59).

6.61. Опишите перестановку размера N (набор значений для массива а), для которой условие a[i] != i в процессе работы программы 6.14 выполняется максимальное число раз.

6.62. Докажите, что в процессе перемещения ключей и пустых мест в программе 6.14 мы обязательно вернемся к ключу, с которого начат цикл.

6.63. Реализуйте программу, аналогичную программе 6.14, для сортировки указателей, если указатели указывают на массив из N записей типа Item.