|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Элементарные методы сортировки
Сортировка Шелла
Сортировка вставками работает медленно, поскольку в ней выполняются обмены только соседних элементов, и любой элемент может сдвинуться лишь на одну позицию за один шаг. Например, если элемент с наименьшим ключом оказался в конце массива, потребуется N шагов, чтобы он занял нужное место. Сортировка Шелла (shellsort) представляет собой простое расширение метода вставок, быстродействие которого достигается за счет возможности обмена далеко отстоящих друг от друга элементов.
Идея заключается в переупорядочении файла таким образом, чтобы совокупность его h-ых элементов (начиная с любого) образовывала отсортированный файл. Такой файл называется h-упорядоченным (h-sorted). Другими словами, h-упорядоченный файл представляет собой h независимых, упорядоченных и перемежающихся файлов. В процессе h-сортировки при больших значениях h могут меняться местами элементы массива, расположенные далеко друг от друга — это облегчает последующую h-сортировку при меньших значениях h. Использование такой процедуры для любой последовательности значений h, которая заканчивается значением 1, дает упорядоченный файл. В этом и заключается суть сортировки Шелла.
Один из способов реализации сортировки Шелла заключается в независимой сортировке вставками каждого из h подфайлов для каждого h. Несмотря на очевидную простоту этого процесса, возможен еще более простой подход — именно благодаря независимости подфайлов. В процессе h-сортировки файла каждый элемент просто вставляется среди предшествующих элементов в соответствующем h-подфайле, сдвигая большие элементы вправо (см. рис. 6.8). Для этого применяется сортировка вставками, только в ней перемещение по файлу выполняется увеличением или уменьшением индекса на h, а не на 1. Тогда реализация сортировки Шелла сводится к обычным проходам сортировки вставками, как в программе 6.5, но для ряда приращений h. Работа программы показана на рис. 6.9.
А вот какую последовательность шагов следует использовать? В общем случае на этот вопрос трудно найти правильный ответ.
Программа 6.5. Сортировка Шелла
Если отказаться от использования сигнальных ключей и заменить в сортировке вставками каждое " 1 " на " h " , то полученная программа будет выполнять h-сортировку файла. Добавление внешнего цикла, изменяющего значение шага, дает компактную реализацию сортировки Шелла, в которой используется последовательность шагов 1 4 13 4 0 121 364 1093 3280 9841 . . .
template <class Item>
void shellsort(Item a[], int l, int r)
{ int h;
for (h = 1; h <= (r-l)/9; h = 3*h+1) ;
for ( ; h > 0; h /= 3)
for (int i = l+h; i <= r; i++)
{ int j = i; Item v = a[i];
while (j >= l+h && v < a[j-h])
{ a[j] = a[j-h]; j -= h; }
a[j] = v;
}
}
В литературе опубликованы результаты исследований различных последовательностей шагов, некоторые из них хорошо зарекомендовали себя на практике, однако возможно, что наилучшая последовательность еще не найдена. Обычно на практике используются убывающие последовательности шагов, близкие к геометрической прогрессии, так что число шагов логарифмически зависит от размера файла. Например, если размер следующего шага равен примерно половине предыдущего, то для сортировки файла из 1 миллиона элементов потребуется примерно 20 шагов, если отношение примерно равно четверти, то достаточно 10 шагов.
В верхней части данной диаграммы показан процесс 4-сортировки файла из 15 элементов. Сначала выполняется сортировка вставками подфайла в позициях 0, 4, 8, 12, затем сортировка вставками подфайла в позициях 1, 5, 9, 13, потом сортировка вставками подфайла в позициях 2, 6, 10, 14 и, наконец, сортировка вставками подфайла в позициях 3, 7, 11. Но все четыре подфайла независимы друг от друга, так что тот же результат можно получить, вставляя каждый элемент в соответствующую позицию в его подфайле и перемещаясь назад шагами через четыре элемента (внизу). Нижняя диаграмма получается из первых рядов каждой части верхней диаграммы, затем из вторых рядов каждой части и т.д.
Сортировка файла при помощи 13-сортировки (сверху), затем 4-сортировки (в центре) и 1-сортировки (внизу) не требует выполнения большого количества сравнений (судя по количеству неза-штрихованных элементов). Завершающий проход — обычная сортировка вставками, но при этом ни один из элементов не перемещается далеко, в силу упорядоченности, внесенной двумя первыми проходами.
Использование минимального числа шагов — важное требование, но необходимо учитывать различные арифметические соотношения между шагами, такие как величина их общих делителей и другие свойства. Практически хорошая последовательность шагов может повысить быстродействие алгоритма процентов на 25, но сама задача представляет собой увлекательную загадку — пример неожиданно сложного аспекта у вроде бы простого алгоритма. Последовательность шагов 1 4 13 40 121 364 1093 3280 9841 . . . , используемая в программе 6.5, с отношением соседних шагов примерно в одну треть, была рекомендована Кнутом в 1969 г. (см. раздел ссылок). Она просто вычисляется (начав с 1, следующее значение шага равно утроенному предыдущему плюс 1) и обеспечивает довольно эффективную сортировку даже в случае относительно больших файлов (см. рис. 6.10).
Многие другие последовательности шагов позволяют получить еще более эффективную сортировку, однако программу 6.5 трудно ускорить более чем на 20% даже в случае сравнительно больших значений N. Одной из таких последовательностей является 1 8 2 3 77 281 1073 4193 16577 . . . , т.е. последовательность 4i+1 + 3 • 2i + 1 для i > 0 , которая, похоже, работает быстрее в худшем случае (см. лемму 6.10). На рис. 6.11 показано, что эта последовательность — а также последовательность Кнута и многие другие последовательности шагов — обладают похожими динамическими характеристиками для файлов больших размеров. Вполне возможно, что существуют лучшие последовательности. Несколько идей по улучшению последовательностей шагов рассматриваются в упражнениях.
Но существуют и плохие последовательности шагов: например, 1 2 4 8 16 32 64 128 256 512 1024 2048 ... (первоначальная последовательность, предложенная Шеллом еще в 1959 г. (см. раздел ссылок)), обычно приводит к низкой производительности, поскольку элементы в нечетных позициях не сравниваются с элементами в четных позициях вплоть до последнего прохода. Этот эффект заметен для случайно упорядоченных файлов и становится катастрофическим в худшем случае: время выполнения вырождается до квадратичного, если, например, половина элементов с меньшими значениями находится в четных позициях, а половина элементов с большими значениями — в нечетных позициях (см. упражнение 6.36).
Программа 6.5 вычисляет следующий шаг, разделив текущий шаг на 3 после инициализации, гарантирующей использование одной и той же последовательность шагов. Другой вариант — начать сортировку с h = N/3 или с какой-то другой функции от N. Но лучше избегать таких стратегий, т.к. некоторые значения N могут дать плохие последовательности шагов наподобие описанной выше.
Наше описание эффективности сортировки Шелла не отличается особой точностью, поскольку никто не смог выполнить анализ данного алгоритма. Этот пробел в наших знаниях затрудняет не только вычисление различных последовательностей шагов, но и аналитическое сравнение сортировки Шелла с другими методами.
Каждый проход сортировки Шелла вносит упорядоченность в файл как целое. Сначала выполняется 40-сортировка файла, затем 13-сортировка, потом 4-сортировка, и, наконец, 1-сортировка. Каждый проход приближает файл к окончательному состоянию.
Не известно даже функциональное выражение для времени выполнения сортировки Шелла (более того, это выражение зависит от выбора последовательности шагов). Кнут обнаружил, что неплохо описывают ситуацию функциональные формы
N (logN)2 и N1,25
, а дальнейшие исследования показали, что некоторые виды последовательностей описываются более сложными выражениями вида 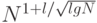 .
.
В завершение текущего раздела отвлечемся от основной темы и рассмотрим некоторые известные результаты исследования сортировки методом Шелла. Наша основная цель — показать, что даже простые с виду алгоритмы могут обладать сложными свойствами, а анализ алгоритмов не только имеет практическое значение, но и может представлять собой интересную научную задачу. Приведенная ниже информация может оказаться полезной читателям, которых заинтересовал поиск новых, более удачных последовательностей шагов сортировки Шелла; остальные могут сразу перейти к разделу 6.7.
Лемма 6.7. В результате h-сортировки k-упорядоченного файла получается h- и k-упорядоченный файл.
Доказать этот вроде бы очевидный факт совсем не просто (см. упражнение 6.47). 
Лемма 6.8. Сортировка Шелла выполняет менее N(h — 1)(k — 1)/g сравнений при g-сортировке h- и k-упорядоченного файла, если h и k взаимно просты.
Причина этого утверждения показана на
рис.
6.12. Ни один элемент, расположенный дальше (h — 1) (k — 1) позиций слева от любого заданного элемента х, не может быть больше х, если h и k взаимно просты (см. упражнение 6.43). При g-сортировке проверяется не более одного из каждых g таких элементов. 
Лемма 6.9. Сортировка Шелла выполняет менее
O(N3/2) сравнений для последовательности шагов
1 4 13 40 121 364 1093 3280 9841 . . .
Для больших шагов имеются h подфайлов размером N/h, и в худшем случае трудоемкость равна примерно
N2/h
. При малых шагах из леммы 6.8 следует, что трудоемкость составляет приблизительно Nh. Доказательство следует из применения лучшего из этих значений для каждого шага. Лемма справедлива для любой экспоненциально возрастающей последовательности со взаимно простыми членами. 
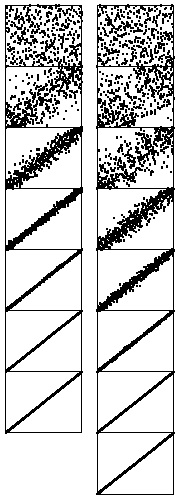
увеличить изображение
Рис. 6.11. Динамические характеристики сортировки Шелла (две различные последовательности шагов)
Представленный на рисунке процесс выполнения сортировки Шелла можно сравнить с закрепленной в углах резиновой лентой, стягивающей все точки ленты к диагонали. Здесь показаны две последовательности шагов: 121 40 13 4 1 (слева) и 209 109 41 19 5 1 (справа). Вторая последовательность требует на один проход больше, но выполняется быстрее, поскольку каждый ее проход более эффективен.
Нижний ряд изображает массив, где заштрихованные квадратики обозначают элементы, которые должны быть меньше или равны крайнему правому элементу, если массив 4- и 13-упорядочен. 4 верхних ряда показывают происхождение нижнего ряда. Если правый элемент находится в массиве в позиции i, то 4-упорядочение означает, что элементы массива в позициях i — 4, i — 8, i — 12, ... меньше или равны ему (верхний ряд). 13-упорядочение означает, что меньше или равен ему элемент i — 13, а вместе с ним, в силу 4-упорядочения, и элементы i — 17, i — 21, i — 25, ... (второй ряд сверху). Аналогично меньше или равен ему элемент в позиции i — 26, а вместе с ним, в силу 4-упорядочения, и элементы i — 30, i — 34, i — 38, ... (третий ряд сверху), и т.д. Оставшиеся незаштрихованными квадратики — те, которые могут быть больше, чем элемент слева; здесь их не более 18 (самый дальний элемент находится в позиции i — 36). Поэтому для сортировки вставками 13- и 4-упорядоченного файла из N элементов нужно выполнить не более 18N сравнений.
Лемма 6.10. Сортировка Шелла выполняет менее O (N4/3) сравнений для последовательности шагов 1 8 23 77 281 1073 4193 16577 . . .
Доказательство этой леммы практически не отличается от доказательства леммы 6.9. Из леммы, аналогичной лемме 6.8, следует, что трудоемкость сортировки для небольших шагов имеет порядок
Nh1/2
. Доказательство этой леммы требует привлечения аппарата теории чисел, что выходит за рамки данной книги (см. раздел ссылок). 
Последовательности шагов, которые рассматривались до сих пор, эффективны потому, что в них соседние элементы взаимно просты. Другое семейство последовательностей шагов эффективно именно благодаря тому, что такие элементы не являются взаимно простыми.
В частности, из доказательства леммы 6.8 следует, что в процессе завершающей сортировки вставками 2- и 3-упорядоченного файла каждый элемент перемещается не более чем на одну позицию. Это значит, что такой файл можно упорядочить одним проходом пузырьковой сортировки (а дополнительный цикл сортировки вставками не нужен). Далее, если файл 4-упорядочен и 6-упорядочен, то каждый элемент также перемещается максимум на одну позицию при его 2-сортировке (поскольку каждый подфайл 2- и 3-упорядочен). И если файл 6-упорядочен и 9-упорядочен, то каждый элемент перемещается не более чем на одну позицию при его 3-сортировке. Продолжая эти рассуждения, мы приходим к идее, которую опубликовал Пратт в 1971 г. (см. раздел ссылок).
Метода Пратта основан на использовании треугольника шагов, причем каждое входящее в этот треугольник число в два раза больше числа, стоящего сверху справа, и в три раза больше числа, стоящего в треугольнике сверху слева.
Если мы используем эти числа снизу вверх и справа налево как последовательность шагов в сортировке Шелла, то каждому шагу х в нижнем ряду предшествуют значения 2х и 3х. Поэтому каждый подфайл оказывается 2-упорядочен и 3-упорядочен, и в процессе всей сортировки ни один элемент не передвигается больше чем на одну позицию!
Лемма 6.11. Сортировка Шелла выполняет менее O(N (logN)2 ) сравнений для последовательности шагов 1 2 3 4 6 9 8 12 18 27 16 24 36 54 81 . . .
Число шагов из треугольника, которые меньше N, определенно меньше (log2N)2. 
Шаги, предложенные Праттом, на практике обычно работают хуже других, поскольку их слишком много. Но этот же принцип позволяет строить последовательности шагов из любых двух взаимно простых чисел h и k. Такие последовательности шагов показывают хорошие результаты, поскольку границы для худших случаев, соответствующие лемме 6.11, дают завышенную оценку трудоемкости для произвольно упорядоченных файлов.
Задача построения хорошей последовательности шагов для сортировки Шелла представляет собой прекрасный пример сложного поведения простых алгоритмов. разумеется, мы не сможем выполнять такой же подробный анализ всех рассматриваемых алгоритмов: и место в книге ограничено, и, как и в случае сортировки Шелла, может понадобиться математический аппарат, выходящий за рамки книги; возможны даже незавершенные исследовательские задачи. Однако многие алгоритмы, рассматриваемые в данной книге, появились в результате интенсивных аналитических и эмпирических исследований, выполненных многими исследователями за несколько последних десятилетий, и мы просто воспользуемся плодами их трудов. Эти исследования показывают, что задача повышения эффективности сортировки может как представлять собой интересную научную проблему, так и давать практическую отдачу, даже в случаях простых алгоритмов. В таблица 6.2 приведены эмпирические данные, которые показывают, что некоторые способы построения последовательностей шагов хорошо работают на практике; относительно короткая последовательность 1 8 23 77 281 1073 4193 16577 . . . — одна из самых простых среди используемых в реализациях сортировки Шелла.
Сортировка Шелла работает в несколько раз быстрее других элементарных методов сортировки, даже если шаги являются степенями 2, а некоторые специальные последовательности шагов ускоряют ее в 5 и более раз. Три лучших последовательности, приведенные в данной таблице, существенно различаются по их построению. Сортировка Шелла вполне пригодна для практического применения даже в случае больших файлов — в отличие от сортировки выбором, сортировки вставками и пузырьковой сортировки (см. таблицу 6.1).
| N | O | K | G | S | P | I |
|---|---|---|---|---|---|---|
| 12500 | 16 | 6 | 6 | 5 | 6 | 6 |
| 25000 | 37 | 13 | 11 | 12 | 15 | 10 |
| 50000 | 102 | 31 | 30 | 27 | 38 | 26 |
| 100000 | 303 | 77 | 60 | 63 | 81 | 58 |
| 200000 | 817 | 178 | 137 | 139 | 180 | 126 |
Обозначения:
| O | 1 2 4 8 16 32 64 128 256 512 1024 2048 . . . | |
| K | 1 4 13 40 121 364 1093 3280 9841 . . . | (лемма 6.9) |
| G | 1 2 4 10 23 51 113 249 548 1207 2655 5843 . . . | (упражнение 6.40) |
| S | 1 8 23 77 281 1073 4193 16577 . . . | (лемма 6.10) |
| P | 1 7 8 49 56 64 343 392 448 512 2401 2744 . . . | (упражнение 6.44) |
| I | 1 5 19 41 109 209 505 929 2161 3905 . . . | (упражнение 6.45) |
Из рис. 6.13 видно, что сортировка Шелла достаточно быстро работает на различных видах файлов, а не только на случайно упорядоченных. Построить файл, на котором сортировка Шелла работает медленно для заданной последовательности шагов — достаточно сложная задача (см. упражнение 6.42). Как уже было сказано, существуют плохие последовательности шагов, при использовании которых сортировка Шелла может выполнить квадратичное количество сравнений в худшем случае (см. упражнение 6.36), однако доказано, что для большого количества других последовательностей этот показатель намного ниже. После выполнения нескольких проходов все эти файлы упорядочены одинаково — значит, время выполнения сортировки не очень чувствительно к виду входных данных.
На представленных диаграммах показана работа сортировки Шелла с последовательностью шагов 2 09 109 41 19 5 1 для равномерного распределения, нормального распределения, почти упорядоченного файла, почти обратно упорядоченного файла и случайно упорядоченного файла с 10 различными значениями ключей (слева направо, сверху). Время выполнения каждого прохода зависит от степени упорядоченности файла перед началом прохода.
Сортировка Шелла хорошо работает во многих приложениях, поскольку она упорядочивает за приемлемое время даже довольно большие файлы и реализуется в виде компактной и легко отлаживаемой программы. В последующих нескольких главах мы ознакомимся с методами сортировки, которые более эффективны, но работают, допустим, лишь в два раза быстрее (а то и меньше) при небольших значениях N и существенно сложнее. В общем, если нужно быстрое решение задачи сортировки, но нет желания возиться с интерфейсом системной сортировки, воспользуйтесь сортировкой Шелла, а потом решите, стоит ли напрягаться, чтобы заменить его более совершенным методом.
Упражнения
6.33. Устойчива ли сортировка Шелла?
6.34. Покажите, как следует реализовать сортировку Шелла с последовательностью шагов 1 8 23 77 281 1073 4193 16577 . . . с непосредственным вычислением последовательных шагов — примерно как в коде для последовательности Кнута.
6.35. Приведите диаграммы, соответствующие рис. 6.8 и рис. 6.9 для ключей E A S Y Q U E S T I O N.
6.36. Определите время выполнения сортировки Шелла с последовательностью шагов 1 2 4 8 16 32 64 128 264 512 1024 2048 . . . для упорядочения файла, состоящего из целых чисел 1, 2, ..., N в нечетных позициях и N + 1, N + 2, ..., 2N в четных позициях.
6.37. Напишите программу-драйвер для сравнения последовательностей шагов сортировки Шелла. Введите последовательности из стандартного ввода (по одной в строке); затем используйте их для сортировки 10 файлов с произвольной организацией длиной N = 100, 1000 и 10000. Подсчитывайте количество сравнений или замеряйте фактическое время выполнения.
6.38. Экспериментально определите, позволяет ли добавление или удаление какого-то шага улучшить последовательность шагов 1 8 23 77 281 1073 4193 16577 . . . для N = 10 000.
6.39. Экспериментально определите значение х, которое обеспечивает минимальное время сортировки случайно упорядоченных файлов, если заменить на х шаг 13 в последовательности 1 4 13 40 121 364 1093 3280 9841 . . . для N= 10000.
6.40. Экспериментально определите значение а, которое обеспечивает минимальное время сортировки случайно упорядоченных файлов для последовательности шагов 1,  ,
,
 ,
,  ,
, 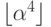 , ... и N = 10 000.
, ... и N = 10 000.
6.41. Найдите последовательность из трех шагов, которая выполняет минимально возможное количество сравнений для случайно упорядоченных файлов, содержащих 1000 элементов.
6.42. Подберите файл из 100 элементов, для которого сортировка Шелла с последовательностью шагов 1 8 2 3 77 выполняет максимальное количество операций сравнения.
6.43. Докажите, что если h и k — взаимно простые числа, то любое число, большее или равное (h — 1)(k — 1), можно представить в виде линейной комбинации h и k с неотрицательными коэффициентами. Совет: покажите, что если любые два из первых h — 1 чисел, кратных k, при делении на h дают при деления на h одинаковый остаток, то h и k должны иметь общий делитель.
6.44. Экспериментально определите значения h и k, которые обеспечивают минимальное время сортировки случайно упорядоченных файлов из 10 000 элементов, если в качестве шагов сортировки используется последовательность, подобная последовательности Пратта, построенная для этих h и k.
6.45. Последовательность шагов 1 5 19 41 109 209 505 929 2161 3905 . . . построена с помощью слияния последовательностей 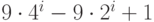 и
и 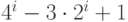 для i > 0. Сравните результаты использования этих последовательностей по отдельности с результатом использования их слияния на примере сортировки 10 000 элементов.
для i > 0. Сравните результаты использования этих последовательностей по отдельности с результатом использования их слияния на примере сортировки 10 000 элементов.
6.46. Последовательность шагов 1 3 7 21 48 112 336 861 1968 4592 13776 . . . получена из последовательности, состоящей из взаимно простых чисел, скажем,
1371641101,с последующим построением треугольника на манер последовательности Пратта. Только теперь i-й ряд треугольника получается умножением первого элемента в (i — 1)-ом ряду на i-й элемент базовой последовательности и умножением каждого элемента в (i — 1)-ом ряду на (i + 1)-й элемент базовой последовательности. Найдите экспериментально базовую последовательность, которая превосходит указанную выше при сортировке 10 000 элементов.
6.47. Завершите доказательства лемм 6.7 и 6.8.
6.48. Напишите реализацию, основанную на алгоритме шейкерной сортировки (упражнение 6.30), и сравните ее со стандартным алгоритмом. Совет: последовательности шагов должны существенно отличаться от последовательностей, применяемых в стандартных алгоритмах.