|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Абстрактные типы данных
Очереди FIFO и обобщенные очереди
Очередь (first-in, first-out - первым пришел, первым ушел, сокращенно FIFO) является еще одним фундаментальным АТД. Она похожа на стек магазинного типа, но с противоположным правилом удаления элемента: из очереди удаляется не последний вставленный элемент, а наоборот - элемент, который был вставлен в очередь раньше всех остальных.
Пожалуй, ящик для студенческих работ у нашего занятого профессора должен бы был функционировать как очередь FIFO, поскольку порядок "первым пришел, первым ушел" интуитивно кажется более справедливым для выбора очередной работы. Однако этот профессор не всегда отвечал на телефонные звонки и даже опаздывал на лекции! В стеке какая-нибудь служебная записка может застрять на дне, но срочные документы обрабатываются сразу же после появления. В очереди FIFO документы обрабатываются по порядку, и каждый должен ожидать своей очереди.
Очереди FIFO часто встречаются в повседневной жизни. Когда мы стоим в цепочке людей, чтобы посмотреть кинокартину или купить продукты, нас обслуживают в порядке FIFO. Аналогично этому в вычислительных системах очереди FIFO часто используются для обслуживания задач, которые необходимо выполнять по принципу "первым пришел, первым обслужен". Другим примером, иллюстрирующим различие между стеками и очередями FIFO, может служить отношение к скоропортящимся продуктам в магазине. Если продавец выкладывает новые товары на переднюю часть полки, и покупатели берут товары также с передней части полки, получается стек. У продавца могут возникнуть неприятности, поскольку товар на задней части полки может стоять очень долго и попросту испортиться. Выкладывая новые товары на заднюю часть полки, продавец гарантирует, что время, в течение которого товар находится на полке, ограничивается временем, необходимым покупателям для приобретения всех товаров, выставляемых на полку. Этот же базовый принцип применяется во множестве подобных ситуаций.
Определение 4.3. Очередь FIFO - это АТД, который содержит две базовых операции: вставить (put - занести) новый элемент и удалить (get - извлечь) элемент, который был вставлен раньше всех остальных.
Программа 4.13 является интерфейсом для АТД очереди FIFO. Этот интерфейс отличается от интерфейса стека, рассмотренного в разделе 4.2, только названиями - для компилятора эти два интерфейса идентичны! Это подчеркивает тот факт, что сама абстракция, которую программисты обычно не определяют формально, является существенным компонентом абстрактного типа данных. Для больших приложений, которые могут содержать десятки АТД, задача их точного определения очень важна. В настоящей книге мы работаем с АТД, представляющими важнейшие понятия, которые определяются в тексте, но не при помощи формальных языков (разве что через конкретные реализации). Чтобы понять природу абстрактных типов данных, потребуется рассмотреть примеры их использования и конкретные реализации.
На рис. 4.6 рис. 4.6 показано, как очередь FIFO изменяется в ходе ряда последовательных операций извлечь и занести. Каждая операция извлечь уменьшает размер очереди на 1, а каждая операция занести увеличивает размер очереди на 1. Элементы очереди перечислены на рисунке в порядке их занесения в очередь, поэтому ясно, что первый элемент списка - это тот элемент, который будет возвращаться операцией извлечь. Опять-таки, в реализации можно организовать элементы любым требуемым способом при условии сохранения иллюзии того, что элементы организованы именно в соответствие с дисциплиной FIFO.
На рисунке показан результат выполнения последовательности операций. Операции представлены в левом столбце (порядок выполнения - сверху вниз); здесь буква обозначает операцию put (занести), а звездочка - операцию get (извлечь). Каждая строка содержит операцию, букву, возвращаемую операцией get, и содержимое очереди от первого занесенного элемента до последнего (слева направо).
Программа 4.13. Интерфейс АТД очереди FIFO
Данный интерфейс идентичен интерфейсу стека магазинного типа из программы 4.4, за исключением имен функций. Эти два АТД отличаются только спецификациями, которые не отражаются в коде интерфейса.
template <class Item>
class QUEUE
{
private:
// Программный код, зависящий от реализации
public:
QUEUE(int);
int empty();
void put(Item);
Item get();
};
В случае реализации АТД очереди FIFO с помощью связного списка, элементы списка хранятся в порядке от первого вставленного до последнего вставленного элемента (см. рис. 4.6). Такой порядок является обратным по отношению к порядку, который применяется в реализации стека; именно такой порядок позволяет создавать эффективные реализации операций с очередями. Как показано на рис. 4.7 и в программе 4.14 (реализация), требуются два указателя на этот список: один на начало списка (для извлечения первого элемента) и второй на его конец (для занесения в очередь нового элемента).
Программа 4.14. Реализация очереди FIFO на базе связного списка
Различие между очередью FIFO и стеком магазинного типа (программа 4.8) состоит в том, что новые элементы вставляются в конец списка, а не в его начало. Поэтому в данном классе хранится указатель tail на последний узел списка, чтобы функция put могла добавлять в список новый узел: этот узел связывается с узлом, на который указывает указатель tail, а затем указатель tail изменяется так, чтобы он указывал уже на новый узел. Функции QUEUE, get и empty повторяют аналогичные функции в реализации стека магазинного типа на базе связного списка из программы 4.8. Поскольку новые узлы всегда вставляются в конец списка, конструктор узлов может обнулять поле указателя каждого нового узла и поэтому принимать только один аргумент.
template <class Item>
class QUEUE
{
private:
struct node
{ Item item; node* next;
node(Item x)
{ item = x; next = 0; }
};
typedef node *link;
link head, tail;
public:
QUEUE(int)
{ head = 0; }
int empty() const
{ return head == 0; }
void put(Item x)
{ link t = tail;
tail = new node(x);
if (head == 0)
head = tail;
else
t->next = tail;
}
Item get()
{ Item v = head->item;
link t = head->next;
delete head;
head = t;
return v; }
};
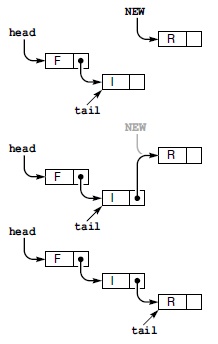
В представлении очереди в виде связного списка новые элементы вставляются в конец списка, поэтому элементы связного списка располагаются от первого вставленного элемента (в начале) до последнего (в конце). Очередь представляется двумя указателями: head (начало) и tail (конец), которые указывают, соответственно, на первый и последний элемент. Для извлечения элемента из очереди удаляется элемент в начале очереди - так же, как и в случае стека (см. рис. 4.5). Чтобы занести в очередь новый элемент, в поле ссылки узла, на который ссылается указатель tail, заносится указатель на новый элемент (в середине рисунка), а затем изменяется указатель tail (внизу).
Для реализации очереди FIFO можно использовать и массив, однако при этом необходимо соблюдать осторожность и обеспечить, чтобы время выполнения как операции занести, так и операции извлечь было постоянным. Это условие запрещает пересылать элементы очереди внутри массива, как это можно было бы предположить при буквальной интерпретации рис. 4.6. Поэтому, как и в реализации на базе связного списка, нам потребуются два индекса массива: для начала очереди и для конца. Содержимым очереди считаются элементы между этими двумя индексами. Чтобы извлечь элемент, он удаляется из начала очереди, после чего индекс head увеличивается на единицу; чтобы занести элемент, он добавляется в конец очереди, а индекс tail увеличивается на единицу. Как показано на рис. 4.8, в результате выполнения последовательности операций занести и извлечь все выглядит так, будто очередь движется по массиву. При достижении конца массива выполняется переход к его началу. Соответствующая реализация приведена в коде программы 4.15.
Лемма 4.2. Для АТД очереди FIFO можно реализовать операции извлечь и занести с постоянным временем выполнения, используя либо массивы, либо связные списки.
Это понятно из анализа кода программ 4.14 и 4.15. 
Здесь приведена последовательность операций с данными для абстрактного представления очереди из рис. 4.6. Очередь реализована за счет запоминания ее элементов в массиве, сохранения индексов начала и конца очереди и возврата индексов на начало массива при достижении его конца. В данном примере индекс tail возвращается на начало массива, когда вставляется второй символ T, а индекс head - когда удаляется второй символ S.
Соображения относительно использования оперативной памяти, которые были изложены в разделе 4.4, применимы и к очередям FIFO. Представление на базе массива требует резервирования объема памяти, достаточного для запоминания максимально ожидаемого количества элементов очереди. В случае же представления на базе связного списка объем необходимой памяти пропорционален числу элементов в структуре данных, но за счет дополнительного расхода памяти на ссылки и дополнительного времени на выделение и освобождение памяти для каждой операции.
По причине фундаментальной взаимосвязи между стеками и рекурсивными программами (см. "Рекурсия и деревья" ), стеки встречаются чаще, чем очереди FIFO, но существуют и алгоритмы, для которых естественными базовыми структурами данных являются очереди. Как уже отмечалось, очереди и стеки используются в вычислительных приложениях чаще всего для того, чтобы отложить выполнение того или иного процесса. Хотя многие приложения, использующие очередь отложенных задач, работают корректно вне зависимости от правила удаления элементов, общее время выполнения программы или объем других необходимых ресурсов может зависеть от этого. Когда в подобных приложениях встречается большое количество операций вставить или удалить, выполняемых над структурами данных с большим числом элементов, различия в производительности очень важны. Поэтому в настоящей книге столь существенное внимание уделяется таким АТД. Если бы производительность программ не интересовала нас, можно было бы создать один единственный АТД с операциями вставить и удалить; однако производительность является предельно важным показателем, поэтому каждое правило, в сущности, определяет отдельный АТД. Чтобы оценить эффективность конкретного АТД, требуется учитывать затраты двух видов: затраты, обусловленные реализацией, которые зависят от выбранных алгоритмов и структур данных, и затраты, обусловленные конкретным правилом принятия решений, в смысле его влияния на производительность клиентской программы. Ниже в данном разделе будут описаны несколько таких АТД, которые будут подробно рассмотрены в последующих главах.
Программа 4.15. Реализация очереди FIFO на базе массива
К содержимому очереди относятся все элементы массива, расположенные между индексами head и tail, учитывая возврат к 0 с конца массива. Если индексы head и tail равны, очередь считается пустой, однако если они стали равными в результате выполнения операции put, очередь считается полной. Как обычно, проверка на такие ошибочные ситуации не выполняется, но размер массива задается на 1 больше максимального количества элементов очереди, ожидаемое клиентом. При необходимости программу можно расширить, включив в нее такие проверки.
template <class Item>
class QUEUE
{
private:
Item *q; int N, head, tail;
public:
QUEUE(int maxN)
{ q = new Item[maxN+1];
N = maxN+1; head = N; tail = 0; }
int empty() const
{ return head % N == tail; }
void put(Item item)
{ q[tail++] = item; tail = tail % N; }
Item get()
{ head = head % N; return q[head++]; }
};
И стеки магазинного типа, и очереди FIFO являются частными случаями более общего АТД: обобщенной (generalized) очереди. Частные случаи обобщенных очередей различаются только правилами удаления элементов. Для стеков это правило "удалить элемент, который был вставлен последним", для очередей FIFO - правило "удалить элемент, который был вставлен первым"; существует и множество других вариантов.
Простым, но, тем не менее, мощным вариантом является неупорядоченная очередь (random queue) с правилом "удалить случайный элемент" - программа-клиент может ожидать, что она с одинаковой вероятностью получит любой из элементов очереди. Используя представление на базе массива (см. упражнение 4.48), для неупорядоченной очереди можно реализовать операции с постоянным временем выполнения. Это представление на базе массива требует, как для стеков и очередей FIFO, предварительного выделения оперативной памяти. Однако в данном случае альтернативное представление на базе связного списка менее удобно, чем в случае стеков и очередей FIFO, поскольку эффективная реализация как операции вставки, так и операции удаления является очень трудной задачей (см. упражнение 4.49). На базе неупорядоченных очередей можно создавать рандомизированные алгоритмы, которые с высокой степенью вероятности позволяют избежать вариантов наихудшей производительности (см. раздел 2.7 "Принципы анализа алгоритмов" ).
В нашем описании стеков и очередей FIFO элементы упорядочены по времени вставки в очередь. Но можно рассмотреть более абстрактную концепцию - последовательный ряд упорядоченных элементов с базовыми операциями вставки и удаления элементов и в начале, и в конце списка. Если элементы вставляются в конец списка и удаляются также с конца, получается стек (как в реализации на базе массива); если элементы вставляются в начало и удаляются в начале, тоже получается стек (как в реализации на базе связного списка). Если же элементы вставляются в конец, а удаляются в начале, то получается очередь FIFO (как в реализации на базе связного списка). Если элементы вставляются в начало, а удаляются с конца, также получается очередь FIFO (этот вариант не соответствует ни одной из реализаций - для его точной реализации можно было бы изменить представление на базе массива, а вот представление на базе связного списка для этой цели не подойдет, т.к. в случае удалении элементов в конце очереди придется сохранять указатель на конец очереди). Эта точка зрения приводит нас к абстрактному типу данных дека (deque - double-ended queue, двухсторонняя очередь), в котором и вставки, и удаления возможны с обеих сторон. Его реализацию мы оставляем в качестве упражнений (см. упражнения 4.43 - 4.47); заметим, что реализация на базе массива окажется простым расширением программы 4.15, а для реализации на базе связного списка потребуется двухсвязный список, иначе удалять элементы дека можно будет только с одной стороны.
В "Очереди с приоритетами и пирамидальная сортировка" рассматриваются очереди с приоритетами, в которых элементы имеют ключи, а правило удаления элементов имеет вид "удалить элемент с самым маленьким ключом". АТД очереди с приоритетами полезен во множестве приложений, и задача нахождения эффективных реализаций для этого АТД была целью исследований в компьютерных науках в течение многих лет. Важным фактором в исследованиях были распознавание и использование АТД в приложениях: подставив новую реализацию вместо старой в большом и сложном приложении и сравнив результаты, можно сразу же определить, является ли новый алгоритм правильным. Более того, посмотрев, как изменяется общее время выполнения приложения при подстановке новой реализации, можно сразу же определить, является ли новый алгоритм более эффективным, чем старый. Структуры данных и алгоритмы, которые рассматриваются в "Очереди с приоритетами и пирамидальная сортировка" для решения данной задачи, интересны, необычны и эффективны.
В главах с 12 по 16 будут рассмотрены таблицы символов (symbol table). Это обобщенные очереди, в которых элементы имеют ключи, а правило удаления элементов имеет вид "удалить элемент, ключ которого равен данному, если таковой элемент существует". Этот АТД, пожалуй, самый важный из изучаемых, и мы изучим десятки его реализаций.
Каждый из этих АТД порождает ряд родственных, но разных АТД, которые появились в результате внимательного изучения клиентских программ и производительности различных реализаций. В разделах 4.7 и 4.8 и далее в данной книге будут рассмотрены многочисленные примеры изменений в спецификации обобщенных очередей, ведущие к еще более разнообразным АТД.
Упражнения
- 4.36. Найдите содержимое элементов q[0], ..., q[4] после выполнения программой 4.15 операций,показанных на рис.4.6. Считайте, что maxN, как и на рис. 4.8 рис. 4.8, равно 10.
-
4.37. В последовательности
a S * Y * Q U E * * * S T * * * I O * N * * *
буква означает операцию занести, а звездочка - операцию извлечь. Найдите последовательность значений, возвращаемых операциями извлечь, если эта последовательность операций выполняется над первоначально пустой очередью FIFO.
- 4.38. Измените приведенную в тексте реализацию очереди FIFO на базе массива (программа 4.15) так, чтобы в ней вызывалась функция error(), если клиент пытается выполнить операцию извлечь, когда очередь пуста, или операцию занести, когда очередь заполнена.
- 4.39. Измените приведенную в тексте реализацию очереди FIFO на базе связного списка (программа 4.14) так, чтобы в ней вызывалась функция error(), если клиент пытается выполнить операцию извлечь, когда очередь пуста, или если при выполнении new для операции занести отсутствует доступная память.
-
4.40. В последовательности
E A s + Y + Q U E * * + s t + * + I O * n + + *
прописные буквы означают операцию занести в начале дека, строчные буквы - операцию занести в конце дека, знак плюс означает операцию извлечь в начале, а звездочка - операцию извлечь в конце. Найдите последовательность значений, возвращаемых операциями извлечь, если эта последовательность операций выполняется над первоначально пустым деком.
- 4.41. При тех же условиях, что и в упр. 4.40, расставьте в последовательности E a s Y плюсы и звездочки так, чтобы операции извлечь возвращали следующую последовательность символов: (1) E s a Y, (2) Y a s E, (3) a Y s E, (4) a s Y E; либо в каждом случае докажите, что такая последовательность невозможна.
- 4.42. Приведите алгоритм, позволяющий определить для двух данных последовательностей, можно ли в первую последовательность вставить плюсы и звездочки так, чтобы, интерпретируя ее как последовательность операций над деком в смысле упр. 4.41, получить вторую последовательность.
- 4.43. Напишите интерфейс для АТД дека.
- 4.44. Напишите реализацию для интерфейса дека (упр. 4.43), в которой в качестве базовой структуры данных используется массив.
- 4.45. Напишите реализацию для интерфейса дека (упр. 4.43), в которой в качестве базовой структуры данных используется двухсвязный список.
- 4.46. Напишите реализацию для приведенного в тексте интерфейса очереди FIFO (программа 4.13), в которой в качестве базовой структуры данных используется циклический список.
- 4.47. Напишите программу-клиент для тестирования АТД дека (упр. 4.43), которая считывает из командной строки в качестве первого аргумента строку команд, подобную приведенной в упр. 4.40, после чего выполняет указанные операции. В интерфейс и реализации добавьте функцию-член dump и выводите содержимое дека после каждой операции, как это сделано на рис. 4.6.
- 4.48. Создайте АТД неупорядоченной очереди (напишите интерфейс и реализацию), в котором в качестве базовой структуры данных используется массив. Обеспечьте для каждой операции постоянное время выполнения.
- 4.49. Создайте АТД неупорядоченной очереди (напишите интерфейс и реализацию), в котором в качестве базовой структуры данных используется связный список. Напишите как можно более эффективные реализации операций вставить и удалить, и оцените затраты на их выполнение для наихудшего случая.
- 4.50. Напишите программу-клиент, которая выбирает для лотереи числа следующим образом: заносит в неупорядоченную очередь числа от 1 до 99, а затем выводит результат удаления пяти чисел.
- 4.51. Напишите программу-клиент, которая принимает из первого аргумента командной строки целое число N, а затем выводит результат раздачи карт на N игроков в покер. Для этого она должна занести в неупорядоченную очередь N элементов (см. упр. 4.7) и затем выдавать результат выбора из этой очереди по пять карт за один раз.
- 4.52. Напишите программу решения задачи связности. Для этого она должна вставлять все пары в неупорядоченную очередь, а затем извлекать их из очереди с помощью алгоритма взвешенного быстрого поиска (программа 1.3).