Диаграммы
Неполные и неразрешимые теории
Предыдущий раздел мог создать впечатление, что наугад взятая теория скорее всего окажется полной, разрешимой, а возможно, и конечно аксиоматизируемой. Это совсем не так.
Откуда вообще берутся в математике аксиоматические теории? Иногда мы пытаемся построить аксиоматически теорию какой-то конкретной структуры (скажем, теорию действительных чисел со сложением и умножением). В других случаях мы стараемся выделить общие свойства различных структур. Например, аксиомы группы фиксируют общие свойства различных групп, и с самого начала ясно, что такая теория не должна и не может быть полной. То же самое можно сказать и про теорию линейно упорядоченных множеств — полнота такой теории означала бы, что все линейно упорядоченные множества (или группы) элементарно эквивалентны, то есть обладают одними и теми же свойствами, выражаемыми формулами. Это, конечно, не так.
Что касается конкретных структур, то и для них естественные
теории не всегда оказываются полными. Классический пример —
натуральные числа со сложением и умножением. Для них имеется
естественная формальная теория (называемая формальной
арифметикой). Ее аксиомы включают в себя обычные свойства
сложения и умножения, а также аксиомы индукции. Опыт показывает,
что любое рассуждение теории чисел, в котором речь идет только о
конечных объектах, может быть формально записано в виде вывода
из аксиом этой теории. Более того, многие доказательства,
использующие бесконечные объекты (скажем, важнейшую в теории
чисел  -функцию Римана), могут быть модифицированы
и погружены в эту формальную теорию. Тем не менее эта теория
неполна (и не может быть полна, как мы увидим в этом разделе).
-функцию Римана), могут быть модифицированы
и погружены в эту формальную теорию. Тем не менее эта теория
неполна (и не может быть полна, как мы увидим в этом разделе).
Среди естественных неполных теорий бывают разрешимые и неразрешимые. Например, теория линейно упорядоченных множеств разрешима, теория абелевых групп разрешима, а теория групп неразрешима. Подробный рассказ об этом далеко выходит за рамки нашей книжки; написанный М.О.Рабином обзор соответствующих результатов можно найти в справочнике по математической логике (часть III, Теория рекурсии [26], глава 4).
Мы же ограничимся тремя примерами (теория равенства, теория полугрупп, формальная арифметика).
Теория равенства
Рассмотрим сигнатуру, содержащую единственный двуместный предикат равенства, и теорию, состоящую из трех аксиом равенства (рефлексивность, симметричность и транзитивность). Эти аксиомы рассматривались в разделе "Аксиомы равенства"; заметим, что у нас нет других предикатных и функциональных символов (и связанных с ними аксиом равенства).
Моделями этой теории являются всевозможные множества с отношениями эквивалентности. Нормальными моделями этой теории являются множества различной мощности; поскольку никакой дополнительной структуры нет, такая модель определяется мощностью (с точностью до изоморфизма). Теоремами этой теории будут формулы с равенством, истинные в множествах любой мощности.
Теорема 68.Множество теорем теории равенства является разрешимым.
Заметим, что истинность формулы в нормальной модели может
зависеть от ее мощности. Например, формула  ложна в одноэлементной модели и истинна во всех
остальных. Поэтому процедура элиминации кванторов в чистом виде
здесь неприменима.
ложна в одноэлементной модели и истинна во всех
остальных. Поэтому процедура элиминации кванторов в чистом виде
здесь неприменима.
Но идея остается той же. От чего зависит истинность формулы этой сигнатуры (с параметрами)? Во-первых, от значений параметров (важно, какие параметры равны друг другу, а какие нет). Во-вторых, от числа элементов модели. (Если бы этой зависимости не было, то можно было бы написать бескванторную формулу, эквивалентную данной во всех моделях теории.)
Например, формула 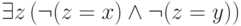 при
при 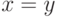 истинна во всех
моделях, начиная с двухэлементной, а при
истинна во всех
моделях, начиная с двухэлементной, а при  истинна во
всех моделях, начиная с трехэлементной. Можно ожидать, что
модели с большим числом элементов неотличимы друг от друга и от
бесконечных моделей.
истинна во
всех моделях, начиная с трехэлементной. Можно ожидать, что
модели с большим числом элементов неотличимы друг от друга и от
бесконечных моделей.
Лемма. Истинность формулы языка с равенством, содержащей  параметров и имеющей кванторную глубину
параметров и имеющей кванторную глубину  ,
определяется тем, какие из параметров равны друг другу, а также мощностью
носителя, при этом все мощности, большие
,
определяется тем, какие из параметров равны друг другу, а также мощностью
носителя, при этом все мощности, большие  , одинаковы.
, одинаковы.
Доказательство леммы проводится индукцией по построению формулы.
Для атомарной (и вообще для любой бескванторной) формулы
мощность вообще не играет роли. Если утверждение леммы верно для
формул 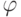 и
и 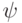 , то оно очевидным образом
верно и для
, то оно очевидным образом
верно и для 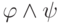 ,
,  ,
,  и
и 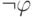 . При этом используется такой факт:
кванторная глубина (число вложенных кванторов) и число
параметров у части формулы не больше, чем у всей формулы.
. При этом используется такой факт:
кванторная глубина (число вложенных кванторов) и число
параметров у части формулы не больше, чем у всей формулы.
Содержательный случай — когда формула начинается с квантора. Когда, скажем, формула
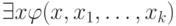
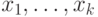 будет истинной (в данной
интерпретации при данных значениях параметров)? Достаточно
попробовать в качестве
будет истинной (в данной
интерпретации при данных значениях параметров)? Достаточно
попробовать в качестве  значения
значения 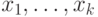 а
также какой-нибудь элемент, отличный от всех этих значений. (Все
такие элементы ничем не отличаются.) Истинность
формулы
а
также какой-нибудь элемент, отличный от всех этих значений. (Все
такие элементы ничем не отличаются.) Истинность
формулы 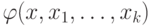 при
при 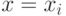 определяется соотношениями между параметрами и мощностью модели (по предположению
индукции; заметим, что число параметров увеличилось на
определяется соотношениями между параметрами и мощностью модели (по предположению
индукции; заметим, что число параметров увеличилось на  , а
кванторная глубина уменьшилась на
, а
кванторная глубина уменьшилась на  , так что сумма осталась
прежней). Существование элемента, отличного от всех
, так что сумма осталась
прежней). Существование элемента, отличного от всех  ,
определяется мощностью модели и числом различных элементов среди
,
определяется мощностью модели и числом различных элементов среди 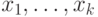 (то есть в конечном счете равенствами вида
(то есть в конечном счете равенствами вида  ). При этом модели всех мощностей, начиная с
). При этом модели всех мощностей, начиная с  , ведут себя одинаково. Кроме того, истинность
формулы
, ведут себя одинаково. Кроме того, истинность
формулы 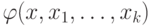 при
при 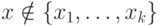 по предположению индукции также
определяется равенствами вида
по предположению индукции также
определяется равенствами вида  и мощностью модели.
и мощностью модели.Квантор всеобщности рассматривается точно так же (а можно его выразить через квантор существования и вообще не рассматривать). Лемма доказана.
Доказательство леммы конструктивно, то есть указывает способ узнать, будет ли формула истинной, если известно, какие ее параметры равны и какова мощность носителя. В частности, для замкнутых формул получаем способ проверять их истинность для всех значений мощности, то есть выводимость в теории равенства.
140. Рассмотрим теорию, в сигнатуре которой есть равенство и конечное число одноместных предикатных символов, а аксиомами являются аксиомы равенства (включая устойчивость предикатов относительно равенства, как в разделе "Аксиомы равенства"). Покажите, что эта теория разрешима.
Эта задача показывает, что добавление одноместных предикатов в сигнатуру не делает теорию равенства неразрешимой. Отметим, что расширение сигнатуры (без изменения множества аксиом) может превратить разрешимую теорию в неразрешимую: например, добавив конечное число одноместных функциональных символов к теории равенства, получим неразрешимую теорию (как видно из доказательства теоремы Черча с помощью проблемы тождества для полугрупп, см. [5]). Добавление одного двуместного предикатного символа также дает неразрешимую теорию.
